最长（非）严格上升/下降子序列 学习笔记

概念

最长（非）严格上升/下降子序列即一个序列中最长的满足每一个数大于（等于） or 小于（等于）前一个数的子序列。这四个概念其实差不多。

做法

以最长（严格）上升子序列为例。原序列为 \([a_1,a_2\cdots a_N]\) ，设 \(f_{i}\) 表示以 \(a_i\) 为结尾的最长上升序列长度，则有：

\[f_{i}=\max\limits_{j<i,a_j\leq a_i}(f_{j})+1 \]

直接转移复杂度为 \(O(N^2)\)

下面有一种 \(O(N\log N)\) 的做法：

设数组 \(d\) 表示 当前 的最长上升子序列， \(len\) 表示其长度。那么 \(d_{len}\) 就表示当前最长上升子序列的最后一个元素。

一开始 \(len=1,d_{len}=a_1\) ，之后开始向后遍历，考虑当前遍历到的 \(a_i\) ：

1. 若 \(a_{i}\geq d_{len}\) ，则直接放入 \(d\) 的末尾
2. 若 \(a_{i}<d_{len}\) ，则在 \(d\) 中找到第一个大于它的数，插入进去，并丢弃在他之后的元素

代码：

scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
d[len=1]=a[1];
for(int i=2;i<=n;i++){
	if(a[i]>d[len]) d[++len]=a[i];
  	else *lower_bound(d+1,d+1+n,a[i]) = a[i];//
}
printf("%d\n",len);

不同类型的最长XX子序列除了改变第四行的运算符号之外，第五行的代码也要相应变化：

最长上升子序列：查找大于等于 lower_bound(...)
最长下降子序列：查找小于等于 upper_bound(...,greater<int>())
最长不下降子序列：查找大于 lower_bound(...)
最长不上升子序列：查找小于 upper_bound(...,greater<int>())

拓展

1. 狄尔沃斯(DilWorth)定理

一个序列的最长（严格/非严格）上升（下降）子序列长度等于其最少可以划分的（非严格/严格）不上升（不下降）子序列的个数。

比如，序列 \(a=[4,3,1,5,7,3]\)

其最长上升子序列长度为 \(3\) ，而它最少可以划分为 \([4,3,1],[5],[7,3]\) 共 \(3\) 个不下降子序列（也有其他情况，但都是3个）

应用：

[NOIP1999]导弹拦截

第一问求的是最长不上升子序列，而第二问求的便是可以将整个序列最少划分成多少个不上升子序列，根据DilWorth定理，直接求最长上升子序列长度即可。

一个序列需要经过多少次修改才能使其变成一个严格上升/下降序列？

答案便是其最长不下降/不上升子序列长度。

证明见： [HAOI2006]数字序列 第一问

若一个序列 \(a\) 的区间 \([l,r]\) 满足 \(|a_{r}-a_{l}|\geq r-l\) （即满足在不更改两端点值的情况下可以将原序列变成严格最长上升序列） ，将其改为严格上升/下降的序列的最小更改幅度是多少？（更改幅度即每个改变的数与之前的值的差）

必定有一个在 \([l,r]\) 内的点 \(k\) 满足修改后的序列为 \(\forall i,l\leq i\leq k,a_i=a_l,\forall j,k+1\leq r,a_j=a_r\) 的情况下更改幅度最小。

修改后的序列：

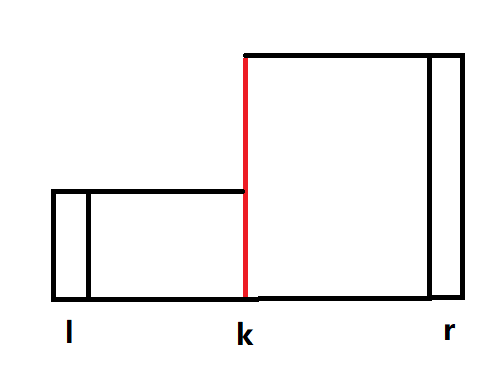
具体实现见： [HAOI2006]数字序列 第二问