虚树 学习笔记

概念

举个栗子： SDOI2011 消耗战

题目大意：有一棵 \(N(N\leq 2.5\times 10^5)\) 个点、根为 \(1\) 的有根树，每一条边有一个边权\(w_i\) ，现有 \(m(m\leq 5\times 10^5)\) 次询问，第 \(i\) 次询问给出 \(k_i(\sum k_i \leq 5\times 10^5)\) 个关键点，现在删除一些边，使得 \(k_i\) 个关键点都与根不联通，问删除的边的最小边权和（询问之间无关联）。

显然可以在原树上跑 \(M\) 次DP，这样的复杂度是 \(O(NM)\) ，显然会超时。

这时我们可以发现，在DP过程中，非关键节点的转移大多是没有必要的，又注意到 \(\sum k_i\) 很小，只有 \(5\times 10^5\) ，因此我们可以考虑 尽量 只在关键节点上跑DP，非关键节点尽量不去管。

顺着这个思路，就有了我们的虚树——即一棵以关键点及其 相关节点 构成的树，其节点树会大大减小，在这棵树上跑树形DP可以大大提高效率。

做法

我们先要思考虚树上应该有哪些节点。

首先，根节点作为储存最终答案的节点，应当放在虚树中。

接着我们考虑剩下的节点，假设原先的树长这样：(红色点为关键点)

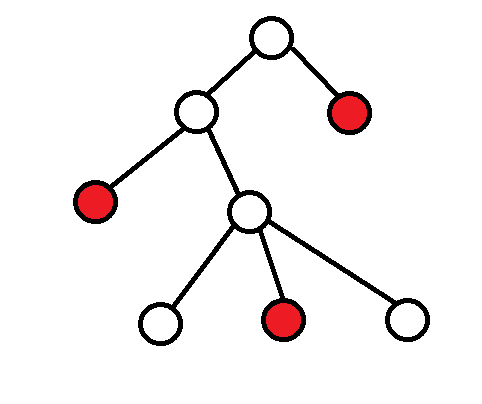
如果我们直接将所有关键点按照原顺序连接起来的话，那么虚树就会长成这个样：

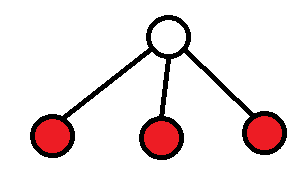
显然树的结构（对DP的影响）改变了，所有不同子树的关键节点都跑到一棵子树上了，答案肯定会改变。因此，我们可以将它们的 LCA 一同加入虚树：

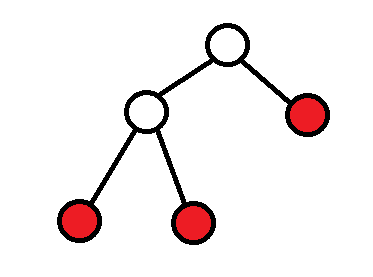
这样可以在树的结构不变的情况下减少无用节点，加速DP

接下来的问题就是如何快速求LCA。不同节点的LCA肯定会大量重复。思考一下那些重复的LCA，都是一个点 \(x\) 及另一个点 \(u\) 的LCA 以及 \(x\) 与 \(u\) 的后代 \(v\) 的LCA，如图：

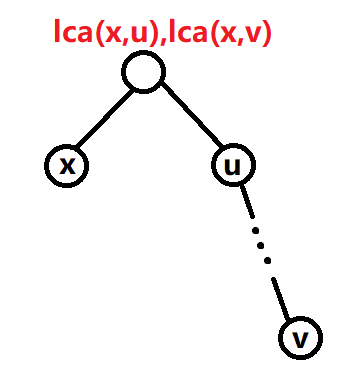
很显然按照DFS序（假设先走x）排序结果为 \(x<u<v\) ，因此我们只需要求出 DFS序 在所有关键点中两两相邻的关键点的LCA即可。

最多一共会加入 \(n-1\) 个LCA，即最终最多会有 \(2n-1\) 个节点。

接下来的问题就在于如何建树。可以发现虚树加入LCA的一大原因就是因为关键节点位于不同子树上，由于我们只需要求DFS序相邻的关键点，因此对于一棵子树而言，仅有最右链（最后遍历的点组成的链）会与下一个子树中的节点产生LCA。因此，我们可以考虑用一个栈来来维护当前的最右链，当前节点假设当前节点为 \(u\) ，若它的上一个节点 \(st_{top}\) 与 \(u\) 在同一条链上（即 \(\operatorname{LCA}(st_{top},u)=st_{top}\) ），就直接将 \(u\) 放在 \(st_{top}\) 的儿子处即可

若 \(st_{top}\) 与 \(u\) 不在同一条链上，就得分几种情况了。

设 \(l=\operatorname{LCA}(st_{top},u)\)

1. 当 \(l\) 在 \(st_{top}\) 与 \(st_{top-1}\) 之间时:

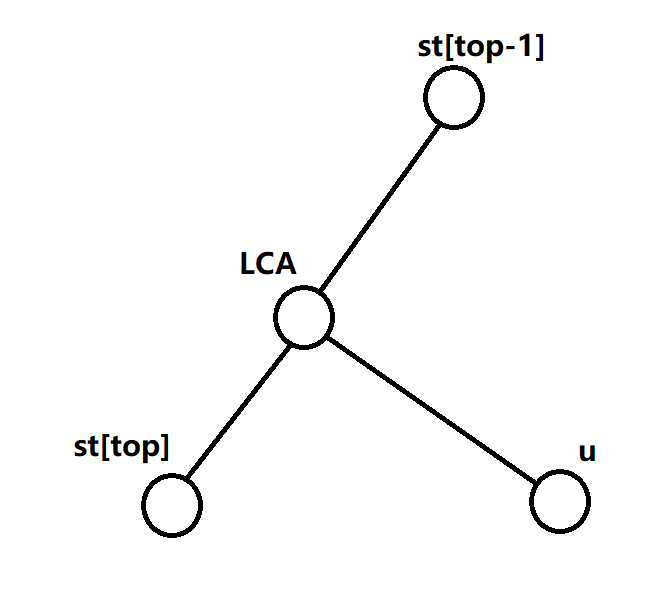
此时最右链的末端由 \(st_{top-1}->l->st_{top}\) 变成了 \(st_{top-1}->l->u\) ，因此我们将 \((st_{top},l)\) 这条边加入虚树，并将 \(st_{top}\) 出栈， \(l\) 和 \(u\) 入栈。

2. 当 \(l=st_{top-1}\) 时：

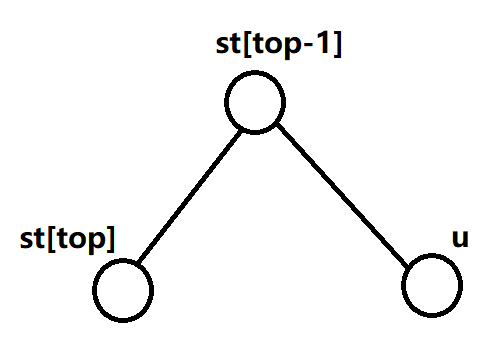
此时最右链也是变成了 \(st_{top-1}->u\) ，与1相同，但是 \(st_{top-1}\) 已经在栈内，因此 \(l\) 不需要入栈。

3. 当 \(l<st_{top-1}\) 时：

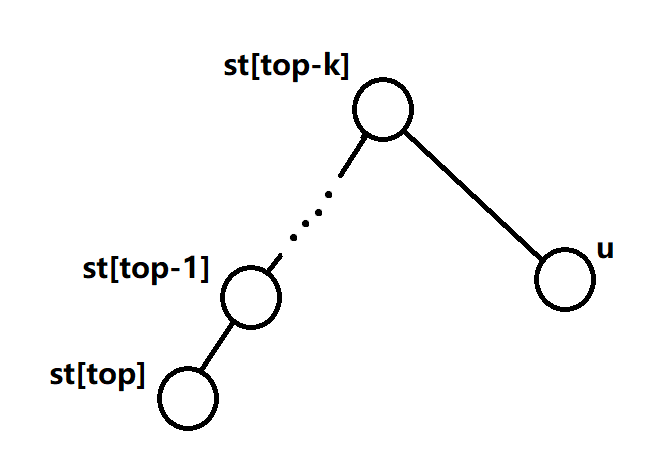
此时 \(l\) 可能是 \(st[top-k]\) 中的任何一个，依旧是将左边的整条链去除，并加入虚树中，最后左边仅剩一个点后当成情况2即可。

依照上述思路做完后，将栈中的最后一条最右链连接好即可。

实现

bool cmp(int a,int b){return id[a]<id[b];}
void Work()
{
	sort(h+1,h+1+k,cmp);//将关键点按照DFS序排序 
	st[top=1]=1,head[1]=-1; 
	//将根节点1放入栈中，并清空与1相连的边（这里沿用了原树的图） 
	for(int i=1;i<=n;i++){
		if(h[i]!=1){
			int l=LCA(h[i],st[top]);//求出当前点与栈顶元素的LCA 
			if(l!=st[top]){//若当前点与栈顶元素不在同一条链上
			
				while(id[l]<id[st[top-1]]){//第三种情况（处理完后变成第二种情况） 
					add(st[top],st[top-1]);
					add(st[top-1],st[top]);
					top--;
				}
				if(id[l]>id[st[top-1]]){//第一种情况 
					head[l]=0;
					add(l,st[top]),add(st[top],l);
					st[top]=l;
				}
				else{//第二种情况 
					add(l,st[top]);
					add(st[top],l);
					top--;
				}
			}
			head[h[i]]=0,st[++top]=h[i];
			//无论是哪一种情况，当前点都是第一次遍历，都要加入栈中
		}
	}
	for(int i=1;i<top;i++){//处理最后一条链 
		add(st[i],st[i+1]);
		add(st[i+1],st[i]);
	}
}

然后跑DP即可。

总结

虚树一般应用于在一棵树上（也有可能是图，要经过转化）选取关键点求解，且关键点数量较小的情况下进行，但同时，DP过程中要注意树的边每个点，每条边的权值变化。

虚树一般和树形DP一起考，虚树本身并没有什么拓展至少我是这么认为的，主要难在建完虚树后如何DP

栗子

1. SDOI2011 消耗战

2. CF613D Kingdom and its cities