hdu6078[优化递推过程] 2017多校4

这道题一眼看过去好像和最长公共子序列有点像。

一开始只想到暴力的推法，

令dp[i][j][k]表示 a[i]=b[j]（即以a_i，b_j为结尾的波浪序列的方案数）， 且最终状态为k(0，1分别代表下降与上升)的方案数。

 

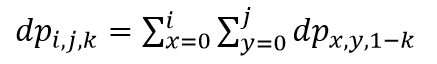
 所以我们可能需要优化一下，用一个sum[i][j][k]表示枚举到a_i时，能构成以b_j为结尾且末状态为k的方案和，可以减少对 j 这一维的枚举。

比如我们在枚举a_i+1时，在遍历b中元素时，如果遇到比a_i+1大的，那么就加上sum[i][j][1]，若遇到比a_i+1小的，就加上sum[i][j][0]，如果等于，就更新答案，把前面所有的可能全部加起来，并更新dp[i+1][j][k]。

/*hdu6078[优化递推过程] 2017多校4*/
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = 998244353LL;
int T, m, n, a[2005], b[2005];
LL sum[2005][3], dp[2005][3];//改为滚动数组, 优化空间
void solve() {
    LL ans = 0;
    for (int i = 1; i <= n; i++) {
        LL up = 1, down = 0;
        for (int j = 1; j <= m; j++) {
            dp[j][0] = dp[j][1] = 0;
            if (b[j] == a[i]) {
                dp[j][0] = up;
                //更新以j为结尾且末状态为波谷的方案数
                dp[j][1] = down;
                //更新以j为结尾且末状态为波峰的方案数
                ans = (ans + up + down) % MOD;
                //更新答案
            }
            else if (b[j] > a[i]) {
                up = (up + sum[j][1]) % MOD;
                //加上以b[j]为结尾且末状态为波峰的方案和
            }
            else down = (down + sum[j][0]) % MOD;
            //加上以b[j]为结尾且末状态为波谷的方案和
        }
        for (int j = 1; j <= m; j++) {
            sum[j][0] = (sum[j][0] + dp[j][0]) % MOD;
            sum[j][1] = (sum[j][1] + dp[j][1]) % MOD;
            //把枚举到a[i]为止，所有以b[j]结尾且末状态为波峰或波谷的方案数加起来
        }
    }
    printf("%lld\n", ans);
}
int main() {
    scanf("%d", &T);
    while (T--) {
        memset(sum, 0, sizeof(sum));
        memset(dp, 0, sizeof(dp));
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
        }
        for (int i = 1; i <= m; i++) {
            scanf("%d", &b[i]);
        }
        solve();
    }
    return 0;
}