RLHF

：此文章由 gpt-4.1 生成，并由人类进行少量修改

PPO

论文：Proximal Policy Optimization Algorithms | arXiv

PPO（Proximal Policy Optimization，近端策略优化）是一种常用的强化学习策略梯度算法，由 OpenAI 于 2017 年提出。它在许多实际应用和基准测试中表现优异，成为了当前深度强化学习领域的主流方法之一。

PPO 的基本思想：

PPO 属于策略优化类方法（Policy Optimization），主要用于训练智能体在环境中学习一个最优策略。它的核心思想是在更新策略时，限制“每一步”策略的变化幅度，从而保证训练过程的稳定性和效率。

相比于传统的策略梯度方法（如 REINFORCE）和基于信赖域的 TRPO（Trust Region Policy Optimization），PPO 通过引入一个“剪切”目标函数，既保持了较高的样本利用率，又避免了 TRPO 复杂的二阶优化。

PPO 的目标函数如下：

\[L^{\text{CLIP}}(\theta) = \mathbb{E}_t \left[ \min \left(r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] \]

其中：

\(\theta\) 表示策略网络的参数。
\(r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\) 是新旧策略概率比。
\(\hat{A}_t\) 是优势函数（Advantage Function）。
\(\epsilon\) 是一个超参数，通常为0.1~0.2，用于限制策略更新的幅度。

clip 操作保证了策略更新不会偏离原策略太远，防止训练不稳定。

PPO 的优势：

实现简单：只需要一阶优化器（如 Adam）即可实现，无需复杂的二阶优化。
训练稳定：通过剪切目标函数保证了策略的平滑更新。
高效：样本利用率高，可以在多个环境中并行采样。

PPO 广泛应用于各种强化学习任务，如游戏（Atari、OpenAI Gym）、机器人控制、自然语言处理等。

简单 PyTorch 实现框架：

import torch as th
import torch.nn as nn
from torch.distributions import Categorical

class PolicyNet(nn.Module):
    def __init__(self, state_dim, action_dim):
        super().__init__()
        self.fc = nn.Sequential(
            nn.Linear(state_dim, 128),
            nn.ReLU(),
            nn.Linear(128, action_dim),
            nn.Softmax(dim=-1)
        )

    def forward(self, x):
        return self.fc(x)

# 优化时使用 PPO 的 clip 损失
# loss = -th.min(ratio * advantages, torch.clamp(ratio, 1-eps, 1+eps) * advantages).mean()

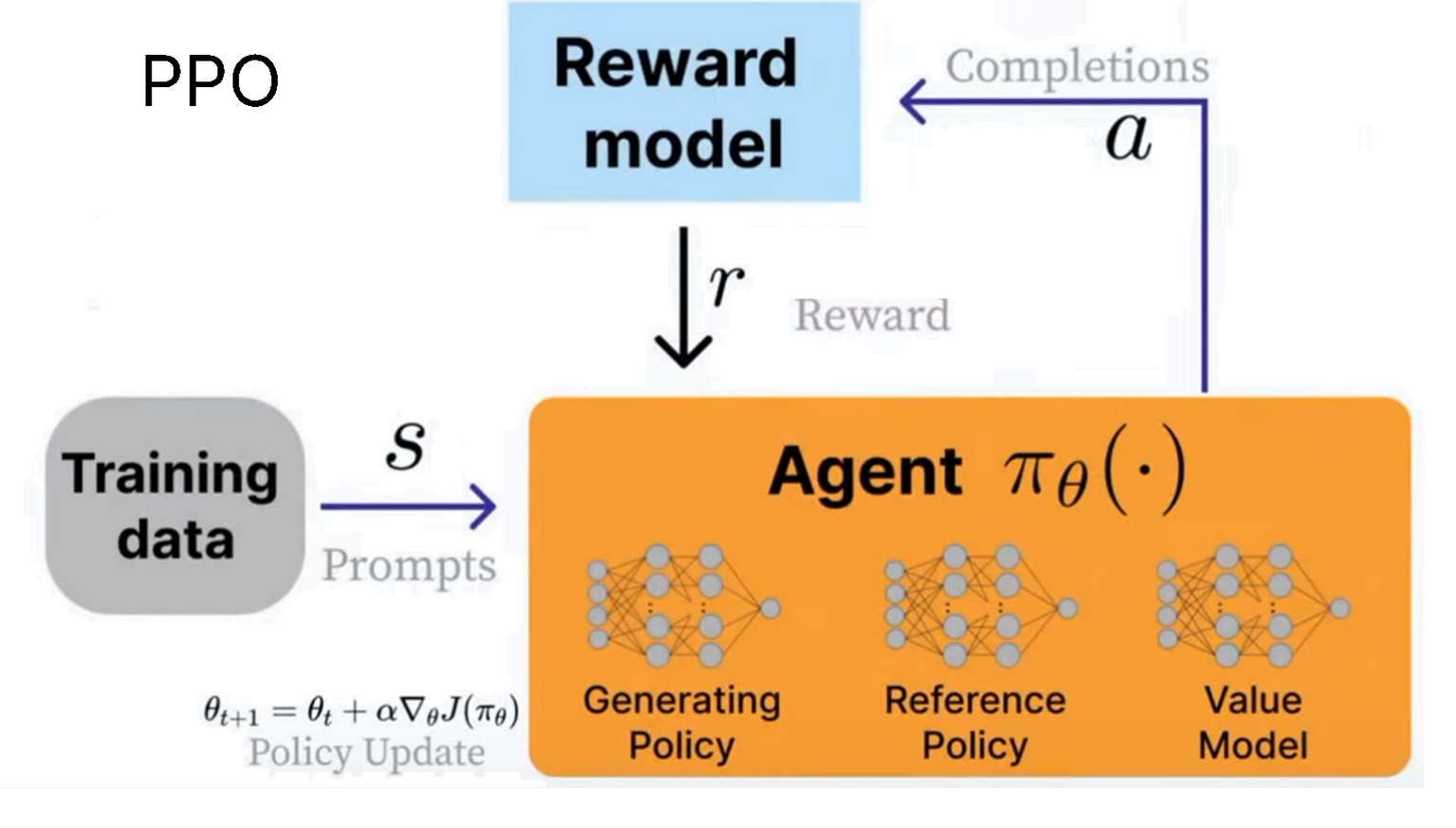
PPO 由三个系统组成：

生成策略（当前训练的模型）
参考策略（原始模型）
价值模型（平均奖励估计器）

我们使用奖励模型来计算当前环境的奖励，目标是最大化奖励。

PPO 的公式看起来很复杂，因为它是为了保持稳定性设计的。

DPO

论文：Direct Preference Optimization: Your Language Model is Secretly a Reward Model | arXiv

在大语言模型训练中，DPO（Direct Preference Optimization，直接偏好优化）是一种强化学习范式，用于直接优化模型输出的偏好顺序。DPO 主要用于对齐（alignment）任务，即让模型更符合人类的偏好。

DPO 的核心思想是：直接使用人类偏好数据（如一组答案 A 和 B，标注人类更喜欢哪个），不需要额外训练奖励模型或使用复杂的强化学习算法（如 PPO）。它通过最大化模型生成偏好输出的概率，并最小化不偏好输出的概率，实现模型的微调。

DPO 的损失函数通常为：

\[L = -\mathbb{E}_{(x, y^+, y^-) \sim D} \left[ \log \frac{\exp(\beta \cdot s_\theta(x, y^+))}{\exp(\beta \cdot s_\theta(x, y^+)) + \exp(\beta \cdot s_\theta(x, y^-))} \right] \]

其中：

\(x\)：输入
\(y^+\)：人类偏好的输出
\(y^-\)：人类不偏好的输出
\(s_\theta(x, y)\)：模型的得分
\(\beta\)：温度参数，控制分布的陡峭程度
\(D\)：带有偏好对的数据集

优点：

训练更直接、更高效、无需奖励模型
更易于实现（可用 PyTorch 实现）

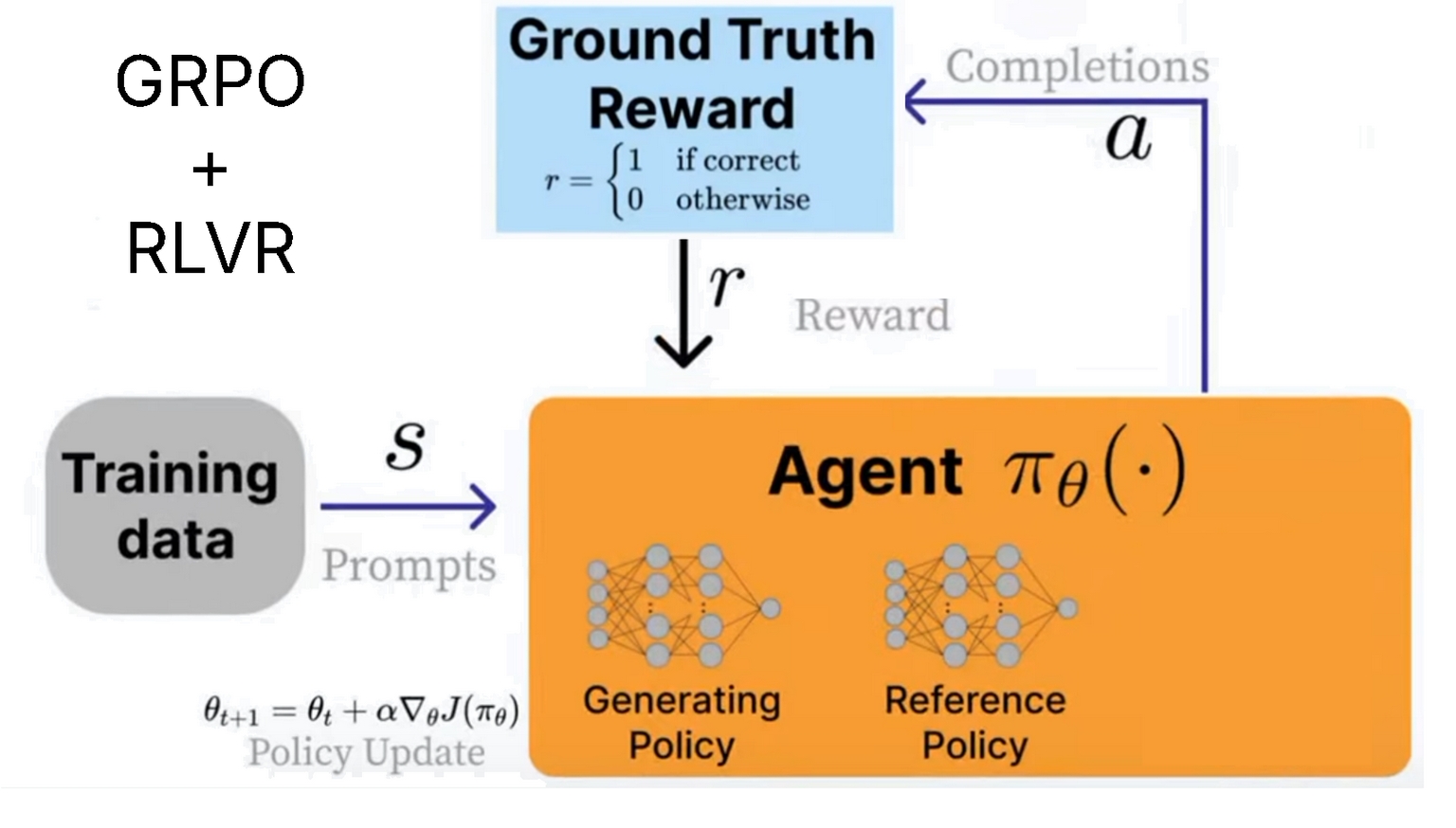
GRPO

论文：DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models | arXiv

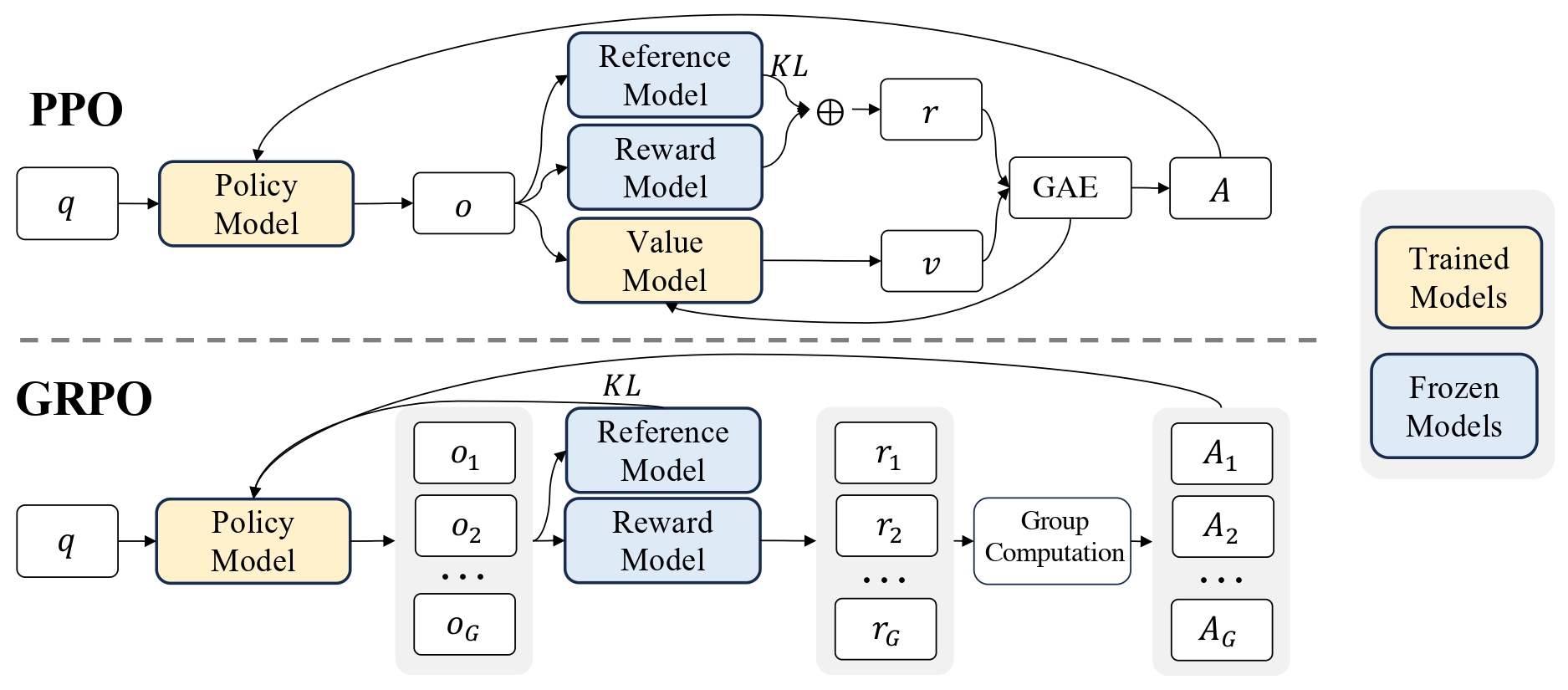
参见：

马尔科夫决策过程

马尔科夫决策过程（Markov Decision Process，MDP）是人工智能和强化学习中用于建模决策问题的数学框架。它可以用来描述一个智能体（agent）在某个环境中，根据当前状态选择动作，并根据动作获得奖励和转移到下一个状态的过程。

组成部分

一个标准的马尔科夫决策过程通常由以下四元组 \((S, A, P, R)\) 组成：

\(S\)：状态空间（States），即所有可能的环境状态的集合。
\(A\)：动作空间（Actions），即智能体在每个状态下可以采取的所有动作的集合。
\(P\)：状态转移概率（Transition Probability），\(P(s' \mid s,a)\) 表示在状态 \(s\) 下采取动作 \(a\) 后转移到状态 \(s'\) 的概率。
\(R\)：奖励函数（Reward Function），\(R(s,a)\) 表示在状态 \(s\) 下采取动作 \(a\) 后获得的即时奖励。

有时还会加上一个折扣因子 \(\gamma \in [0,1]\)，用来权衡当前奖励和未来奖励的重要性。

马尔科夫性

MDP 的核心假设是马尔科夫性，即“无记忆性”：下一个状态和奖励只依赖于当前状态和当前动作，与之前的历史无关。用公式表示为：

\[P(s_{t+1} \mid s_t, a_t, s_{t-1}, a_{t-1}, ..., s_0, a_0) = P(s_{t+1} \mid s_t, a_t) \]

目标

在 MDP 中，智能体的目标是找到一个策略（policy）\(\pi(a \mid s)\)，即在每个状态下选择动作的概率分布，使得累计奖励最大化。累计奖励通常定义为期望的总折扣奖励：

\[G_t = \mathbb{E}\left[ \sum_{k=0}^{\infty} \gamma^k r_{t+k} \right] \]

posted @ 2025-06-09 19:11 Undefined443 阅读(43) 评论(0) 收藏举报

刷新页面返回顶部

undefined443

RLHF

PPO

DPO

GRPO

马尔科夫决策过程

公告