自编码器（Autoencoder）
AE
模型
import torch.nn as nn
class SimpleAE(nn.Module):
def __init__(self):
super().__init__()
# 编码器：将输入数据压缩为更小的表示
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.ReLU(),
nn.Linear(128, 32),
nn.ReLU(),
nn.Linear(32, 8) # 压缩至 8 维
)
# 解码器：重建原始输入数据
self.decoder = nn.Sequential(
nn.Linear(8, 32),
nn.ReLU(),
nn.Linear(32, 128),
nn.ReLU(),
nn.Linear(128, 28*28),
nn.Sigmoid() # 输出在 0~1 之间
)
def forward(self, x):
z = self.encoder(x)
x = self.decoder(z)
return x
训练
import torch as th
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch.optim as optim
# 超参数
batch_size = 128
epochs = 10
# 数据加载
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transforms.ToTensor())
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
device = th.device("cuda" if th.cuda.is_available() else "cpu")
ae = SimpleAE().to(device)
criterion = nn.MSELoss() # 使用均方误差损失
optimizer = optim.Adam(ae.parameters(), lr=1e-3)
ae.train()
for epoch in range(epochs):
total_loss = 0
for sample, _ in train_loader:
input = sample.view(-1, 28*28).to(device) # 展平图片为一维向量
optimizer.zero_grad()
output = ae(input)
loss = criterion(output, input)
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f'Epoch [{epoch+1}/{epochs}], Loss: {total_loss / batch_size:.4f}')
重建
import matplotlib.pyplot as plt
ae.eval()
# 加载测试集
test_dataset = datasets.MNIST('./data', train=False, download=True, transform=transforms.ToTensor())
test_loader = DataLoader(test_dataset, batch_size=4, shuffle=True)
# 取一批数据
data_iter = iter(test_loader)
sample, label = next(data_iter)
# 将图像输入 AE，得到重建图像
with th.no_grad():
input = sample.view(-1, 28*28).to(device)
output = ae(input)
# 显示原始图像与重建图像对比
fig, axes = plt.subplots(2, 4, figsize=(7, 4))
recon = output.view(-1, 28, 28).cpu()
for i in range(4):
axes[0, i].imshow(sample[i].squeeze(), cmap='gray')
axes[0, i].axis('off')
axes[0, i].set_title("Original")
axes[1, i].imshow(recon[i].squeeze(), cmap='gray')
axes[1, i].axis('off')
axes[1, i].set_title("Reconstructed")
plt.show()
生成
with th.no_grad():
z = th.randn(8, 8).to(device) # 在隐变量空间随机采样（高斯分布）
output = ae.decoder(z)
# 显示随机生成的图像
fig, axes = plt.subplots(2, 4, figsize=(7, 4))
sample = output.view(-1, 28, 28).cpu()
for i in range(8):
axes[i // 4, i % 4].imshow(sample[i].squeeze(), cmap='gray')
axes[i // 4, i % 4].axis('off')
plt.suptitle("Randomly Generated Images")
plt.show()
示例代码：SimpleAE | Kaggle
VAE
数学基础
AE 的目标是学到数据的低维表征，而 VAE 认为低维表征服从某个概率分布，并将目标改为学习概率分布的参数，然后从概率分布中采样得到低维表征。为了约束模型学习到的概率分布服从某具体分布，需要用到 KL 散度。为了从分布参数中采样得到样本，需要用到重参数化技巧。
KL 散度
KL 散度用于衡量两个概率分布之间的距离。
假设有两个正态分布 \(P(x)\) 和 \(Q(x)\)，则 \(P\) 相对于 \(Q\) 的 KL 散度定义为：
\[D_{\mathrm{KL}}(P \parallel Q) = \log\frac{\sigma_q}{\sigma_p} + \frac{\sigma_p^2 + (\mu_p - \mu_q)^2}{2\sigma_q^2} - \frac{1}{2}
\]
重参数化
重参数化技巧将随机变量 \(z\sim\mathcal{N}(\mu,\sigma^2)\) 的采样过程分解为一个确定性函数和一个独立于参数的随机变量，使得梯度能够顺利地通过随机节点回传，从而实现有效的梯度估计。其标准形式为：
\[z = \mu + \sigma \odot \epsilon,\quad \epsilon \sim \mathcal{N}(0,1)
\]
这样，虽然 \(z\) 看起来依然是随机的，但实际的随机性被“转移”到了 \(\epsilon\) 上，而 \(\mu\) 和 \(\sigma\) 部分则是一个确定性的可微函数。这样，在反向传播时，就可以直接计算关于 \(\mu\) 和 \(\sigma\) 的梯度，从而优化这些参数。
在 VAE 中，为方便优化，通常令模型直接输出 \(\mu\) 和 \(\log(\sigma^2)\) 而不是 \(\sigma\)（确保方差为正），于是会使用以下形式：
\[z = \mu + e^{\frac{1}{2}\log(\sigma^2)} \cdot \epsilon,\quad \epsilon \sim \mathcal{N}(0,1)
\]
模型
import torch as th
import torch.nn as nn
def reparameterize(mu, logvar):
std = th.exp(0.5 * logvar)
eps = th.randn_like(std)
return mu + std * eps
class SimpleVAE(nn.Module):
def __init__(self):
super().__init__()
# 编码器
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.ReLU(),
nn.Linear(128, 32),
nn.ReLU(),
nn.Linear(32, 16)
)
# 解码器
self.decoder = nn.Sequential(
nn.Linear(8, 32),
nn.ReLU(),
nn.Linear(32, 128),
nn.ReLU(),
nn.Linear(128, 28*28),
nn.Sigmoid()
)
def forward(self, x):
mu, logvar = self.encoder(x).chunk(2, dim=-1)
z = reparameterize(mu, logvar)
x = self.decoder(z)
return x, mu, logvar
损失函数
VAE 的损失函数由两部分组成：
-
重建损失：衡量模型重构数据的能力，通常使用 MSE 或 BCE。（约束解码器还原图像）
-
KL 散度：衡量隐变量的后验分布与先验分布之间的差异。（约束编码器输出符合正态分布的 \(\mu\) 和 \(\log\sigma^2\)）
如果令先验分布 \(p(z) \sim \mathcal{N}(0,1)\)，后验分布 \(q_\phi(z \mid x) \sim \mathcal{N}(\mu,\sigma^2)\)，则可得后验分布 \(q_\phi(z \mid x)\) 对先验分布 \(p(z)\) 的 KL 散度为：
\[D_{\mathrm{KL}}(q_\phi(z \mid x) \parallel p(z)) = -\frac{1}{2}\sum\left[1+\log\sigma^2-\mu^2-\sigma^2\right] \]
import torch.nn.functional as F
def criterion(recon, x, mu, logvar):
MSE = F.mse_loss(recon, x, reduction='sum') # 重建损失
KLD = -0.5 * th.sum(1 + logvar - mu.pow(2) - logvar.exp()) # KL 散度
return MSE + KLD
训练
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch.optim as optim
# 超参数
batch_size = 128
epochs = 10
# 数据加载
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transforms.ToTensor())
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
device = th.device("cuda" if th.cuda.is_available() else "cpu")
vae = SimpleVAE().to(device)
optimizer = optim.Adam(vae.parameters(), lr=1e-3)
vae.train()
for epoch in range(epochs):
total_loss = 0
for sample, _ in train_loader:
input = sample.view(-1, 28*28).to(device)
optimizer.zero_grad()
output, mu, logvar = vae(input)
loss = criterion(output, input, mu, logvar)
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f'Epoch [{epoch+1}/{epochs}], Loss: {total_loss / batch_size:.4f}')
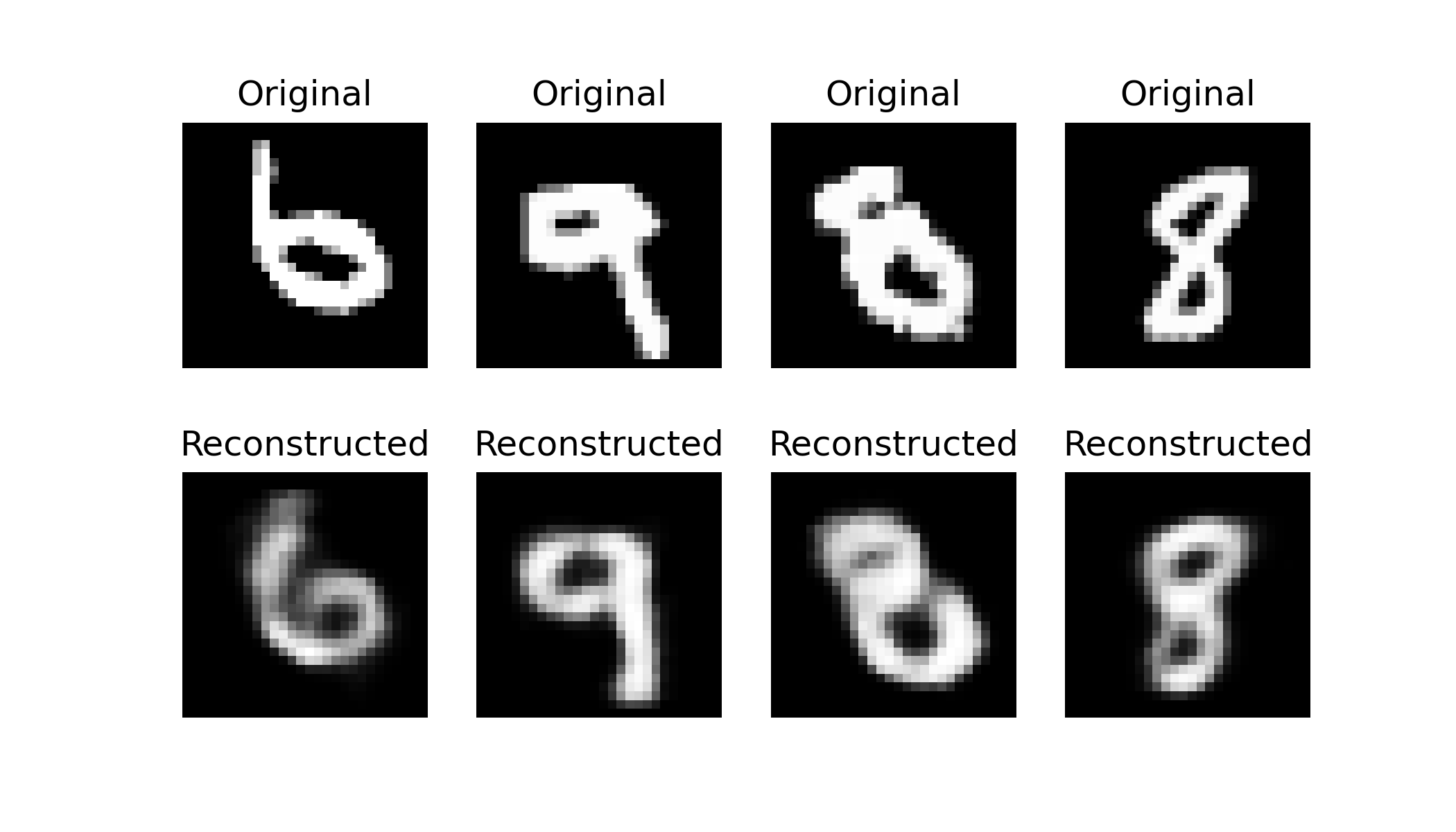
重建
测试已有图像重建效果（定性测试）
import matplotlib.pyplot as plt
vae.eval()
# 加载测试集
test_dataset = datasets.MNIST('./data', train=False, download=True, transform=transforms.ToTensor())
test_loader = DataLoader(test_dataset, batch_size=4, shuffle=True)
# 取一批数据
data_iter = iter(test_loader)
sample, label = next(data_iter)
# 将图像输入 VAE，得到重建图像
with th.no_grad():
input = sample.view(-1, 28*28).to(device)
output, _, _ = vae(input)
# 显示原始图像与重建图像对比
fig, axes = plt.subplots(2, 4, figsize=(7, 4))
recon = output.view(-1, 28, 28).cpu()
for i in range(4):
axes[0, i].imshow(sample[i].squeeze(), cmap='gray')
axes[0, i].axis('off')
axes[0, i].set_title("Original")
axes[1, i].imshow(recon[i].squeeze(), cmap='gray')
axes[1, i].axis('off')
axes[1, i].set_title("Reconstructed")
plt.show()
生成
随机采样生成新图像（从隐空间随机生成）
with th.no_grad():
z = th.randn(8, 8).to(device) # 在隐变量空间随机采样（高斯分布）
output = vae.decoder(z)
# 显示随机生成的图像
fig, axes = plt.subplots(2, 4, figsize=(7, 4))
sample = output.view(-1, 28, 28).cpu()
for i in range(8):
axes[i // 4, i % 4].imshow(sample[i].squeeze(), cmap='gray')
axes[i // 4, i % 4].axis('off')
plt.suptitle("Randomly Generated Images")
plt.show()
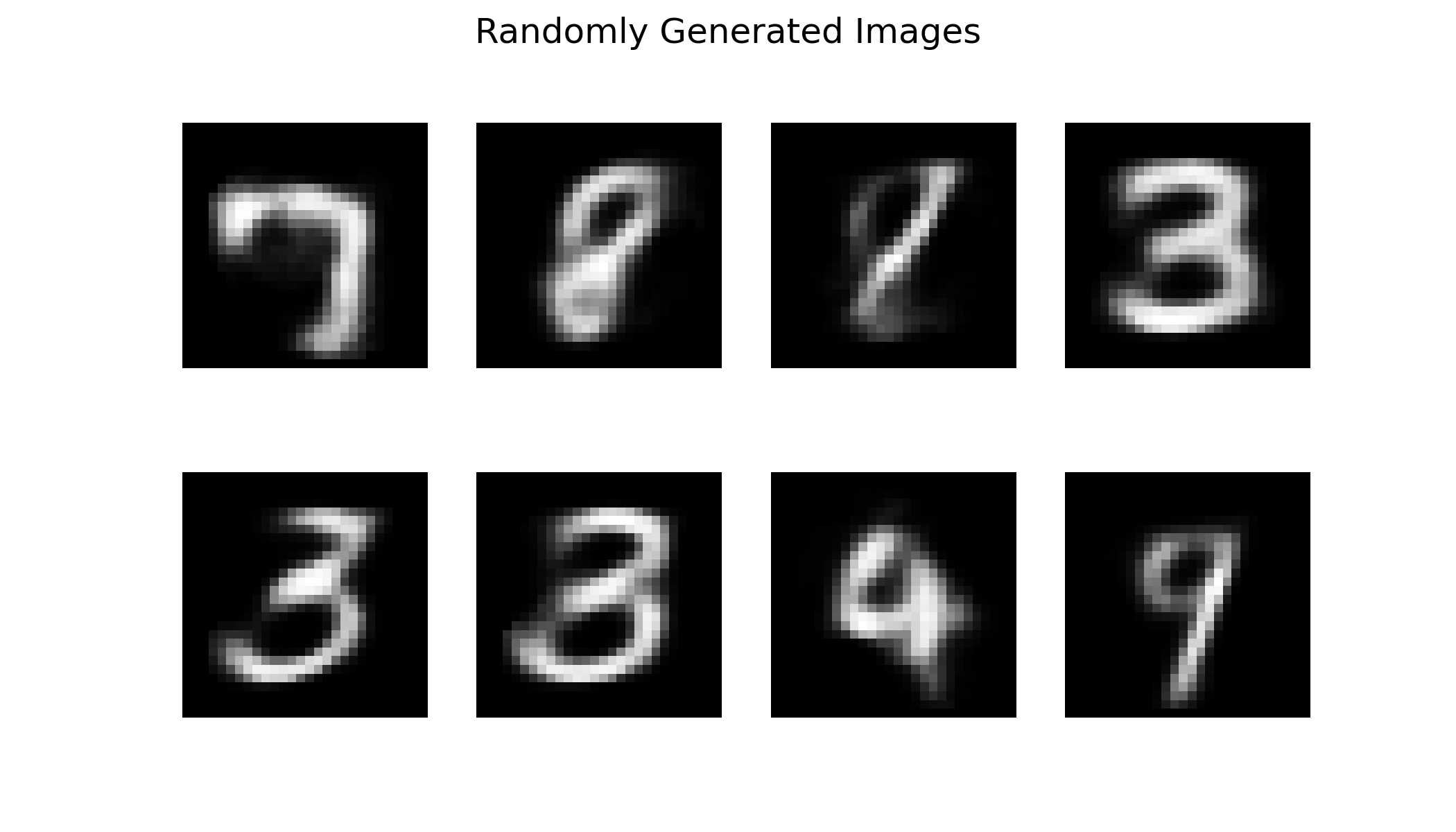
示例代码：SimpleVAE | Kaggle
AE 与 VAE 的区别
| 特点 | AE | VAE |
|---|---|---|
| 网络结构 | 编码器 + 解码器，确定性 | 编码器 + 解码器，概率性 |
| 损失函数 | 重构误差 | 重构误差 + KL 散度 |
| 隐空间表示 | 不一定连续、规则 | 连续、规则 |
| 生成能力 | 弱 | 强（可随机生成） |
| 主要用途 | 降维、重建、去噪 | 数据生成、隐空间插值 |
MAE
Masked Autoencoder
模型
import torch.nn as nn
class SimpleMAE(nn.Module):
def __init__(self):
super().__init__()
# 编码器
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.ReLU(),
nn.Linear(128, 32),
nn.ReLU(),
nn.Linear(32, 8)
)
# 解码器
self.decoder = nn.Sequential(
nn.Linear(8, 32),
nn.ReLU(),
nn.Linear(32, 128),
nn.ReLU(),
nn.Linear(128, 28*28),
nn.Sigmoid()
)
def forward(self, x, mask):
x = x * mask
z = self.encoder(x)
x = self.decoder(z)
return x
随机掩码
import torch as th
def random_mask(x, mask_ratio):
"""随机 mask 生成"""
mask = th.bernoulli(th.full(x.shape, 1 - mask_ratio)).to(x.device)
return mask
说明：
mask_ratio：决定遮挡比例。random_mask：生成和输入同维度的 0/1 mask 张量。- 损失只计算在被遮挡的区域（即 \(1-\text{mask}\) 部分）
训练
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torch.optim as optim
# 超参数
mask_ratio = 0.8 # 遮挡 80% 的像素
batch_size = 128
epochs = 10
# 数据加载
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transforms.ToTensor())
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
# 初始化模型与优化器
device = th.device('cuda' if th.cuda.is_available() else 'cpu')
mae = SimpleMAE().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(mae.parameters(), lr=1e-3)
# 训练
for epoch in range(epochs):
total_loss = 0
for sample, _ in train_loader:
input = sample.view(-1, 28*28).to(device)
mask = random_mask(input, mask_ratio)
optimizer.zero_grad()
output = mae(input, mask)
loss = criterion(output * (1 - mask), input * (1 - mask)) # 只计算遮挡区域的 loss
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f'Epoch [{epoch+1}/{epochs}], Loss: {total_loss / batch_size:.4f}')
重建
import matplotlib.pyplot as plt
mae.eval()
test_dataset = datasets.MNIST('./data', train=False, download=True, transform=transforms.ToTensor())
test_loader = DataLoader(test_dataset, batch_size=4, shuffle=True)
data_iter = iter(test_loader)
sample, label = next(data_iter)
input = sample.view(-1, 28*28).to(device)
mask = random_mask(input, mask_ratio)
# 将图像输入 MAE，得到重建图像
with th.no_grad():
output = mae(input, mask)
# 显示原始图像与重建图像对比
fig, axes = plt.subplots(3, 4, figsize=(7, 6))
masked_sample = (input * mask).view(-1, 28, 28).cpu()
recon = output.view(-1, 28, 28).cpu()
for i in range(4):
axes[0, i].imshow(sample[i].squeeze(), cmap='gray')
axes[0, i].axis('off')
axes[0, i].set_title("Original")
axes[1, i].imshow(masked_sample[i].squeeze(), cmap='gray')
axes[1, i].axis('off')
axes[1, i].set_title("Masked")
axes[2, i].imshow(recon[i].squeeze(), cmap='gray')
axes[2, i].axis('off')
axes[2, i].set_title("Reconstructed")
plt.show()
生成
with th.no_grad():
z = th.randn(8, 8).to(device) # 在隐变量空间随机采样（高斯分布）
output = mae.decoder(z)
# 显示随机生成的图像
fig, axes = plt.subplots(2, 4, figsize=(7, 4))
sample = output.view(-1, 28, 28).cpu()
for i in range(8):
axes[i // 4, i % 4].imshow(sample[i].squeeze(), cmap='gray')
axes[i // 4, i % 4].axis('off')
plt.suptitle("Randomly Generated Images")
plt.show()
- 示例代码：SimpleMAE | Kaggle
- 论文：Masked Autoencoders Are Scalable Vision Learners | arXiv
- PyTorch 实现：facebookresearch/mae | GitHub
- 论文解读：MAE 论文逐段精读【论文精读】| BiliBili
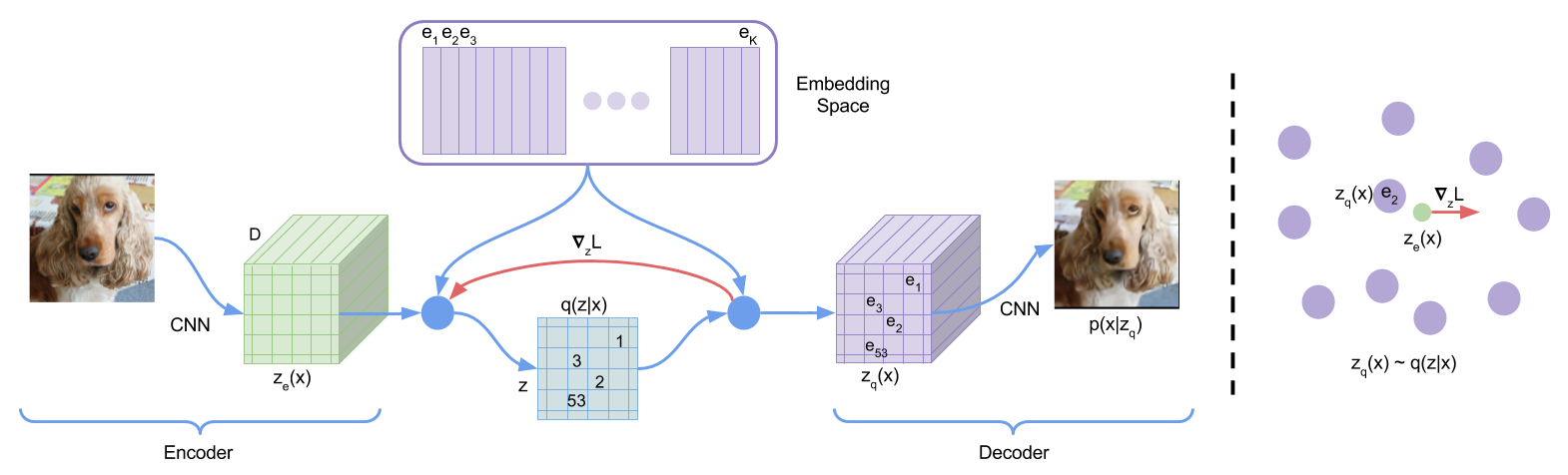
VQ-VAE
Vector Quantised-VAE，向量量化的 VAE。
将图像编码到离散潜空间，而不是连续潜空间。
\[q(z = k \mid x)=
\begin{cases}
1, & \text{for } k = \arg\min_j \| z_e(x) - e_j \|_{2} \\
0, & \text{otherwise}
\end{cases}
\]
- 其中 \(z_e(x)\) 是编码器输出
\[z_q(x) = e_k, \text{ where } k = \arg\min_j \left\| z_e(x) - e_j \right\|_2
\]
直通估计器：直接将解码器的输入（\(z_q(x)\)）的梯度复制到编码器的输出（\(z_e(x)\)）
\[\mathcal{L} = \log p(x \mid z_q(x)) + \|\operatorname{sg}[z_e(x)] - e \|_2^2 + \beta \|z_e(x) - \operatorname{sg}[e] \|_2^2
\]
- 其中 \(\operatorname{sg}\) 代表 stopgradient 运算符，该运算符在前向计算时定义为恒等映射，且其偏导数为零。
- 解码器仅优化第一个损失项，编码器优化第一个和最后一个损失项，嵌入向量由中间的损失项优化。
浙公网安备 33010602011771号