Trigonometric functions

Trigonometric functions

目录

• Trigonometric functions
  • Unit right-angle triangle
  • Unit circleUnit right-angle triangle^[1]
    • convert degree to radian
  • 3. The properties of the trigonometric functions
    • 3.1 signs of trigonometric functions
    • 3.2 periodic functions
    • 3.3 parity
    • 3.4 amplitude

标签（空格分隔）： 三角函数

---

Unit right-angle triangle

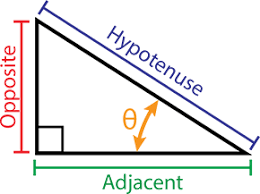
\(\sin\theta=\frac{opposite \quad side}{hypotenuse}\)

\(\cos\theta=\frac{adjacent \quad side}{hypotenuse}\)

\(\tan\theta=\frac{opposite}{adjacent}\)

We can only define how many each trigonometric functions are with \(0\leq\theta\leq180^{\cdot}\).

Unit circleUnit right-angle triangle^[1]

convert degree to radian

Instead, it measures the length of the arc corresponding to the \(\theta\), and the radian \(\theta\) can work!
$180^{\circ}=2\pi $

1 radian = \(\frac{180^{\circ}}{2\pi}\)

we can analogize triangle to circle where \(\theta\) can up to \(360^{\circ}\) or even \(n\times 360^{\circ}\).

\(\sin\theta=\frac{opposite \quad side}{hypotenuse}=y\)

\(\cos\theta=\frac{adjacent \quad side}{hypotenuse}=x\)

\(\tan\theta=\frac{opposite}{adjacent}=\frac{y}{x}\) ^[2]

3. The properties of the trigonometric functions

3.1 signs of trigonometric functions

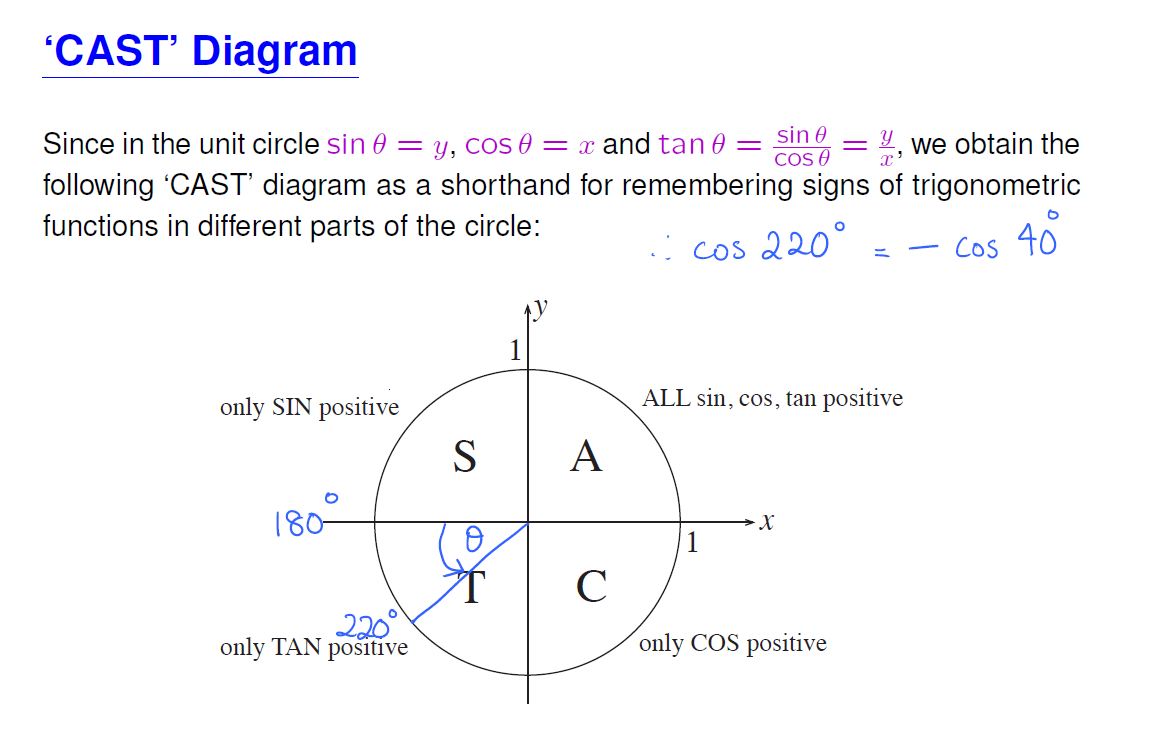
3.2 periodic functions

$f(x)=A\sin(\omega x+\psi) \quad \quad T=\frac{2\pi}{\omega} $
|functions|period|
|sin|\(2\pi\)|
|cos|\(2\pi\)|
|tan|\(\pi\)|

3.3 parity

$\sin $: odd function

$\cos $: even function

$\tan $: odd function

3.4 amplitude

sin && cos ->1
tan -> \(\infty\)

---

1. anchor demo ↩︎

2. tan has no meaning at origin and x =\(k\pi\) ↩︎