ZHX 清北数学 Day3 笔记

ZHX 清北数学 Day3 笔记

一、BSGS 算法（北上广深）

例题：有 $ a^x \bmod p = b $，给定 $ a,b,p $，求 $ x $

暴力：枚举 $ x $

inline int solve (int a, int b, int p) {

    int v = 1;

    for (int x = 0; ; ++ x) {

        if (v == b) return x;

        else v = 1ll * v * a % p;

    }

}

我们考虑到因为 $ p $ 是质数，所以 $ a^{p - 1} \equiv 1 (\text {mod p}) $，又因为 $ a^0 \equiv 1 (\text {mod p}) $，所以发生了循环，我们只需要枚举到 $ p - 1 $ 就行

inline int solve (int a, int b, int p) {

    int v = 1;

    for (int x = 0; x < p; ++ x) {

        if (v == b) return x;

        else v = 1ll * v * a % p;

    }

    return -1;

}

算法思路

考虑把枚举的 $ p - 1 $ 个数分组，每组 $ s $ 个数，这样的话：

  1. $ a^0, a^1, \dots a^{s - 1} $

  2. $ a^s, a^{s + 1}, \dots a^{2s - 1} $

    $ \dots $

这样的话考虑在每组找，第一组没有就找第二组

这样明显还是暴力

但是我们发现，这里第一组和第二组是 $ \times a^s $ 的关系

所以如果第二组出现了 $ b $，那么第一组一定会出现 $ b \times a^{-s} $

再这样我们遍历过第一组了，就可以方便的使用二分确定 $ b \times a^{-s} $ 是否出现过了

代码：

inline int solve (int a, int b, int p) {

    int v = 1;

    set < int > sesese;

    for (int x = 0; x < s; ++ x) {

        sesese.insert (v);

        v = 1ll * v * a % p;

    }

    for (int i = 0; i * s <= p; ++ i) {

        int c = 1ll * b * ksm (ksm (a, i * s, p), p - 2, p);

        if (sesese.count (c) != 0) {

            int v = ksm (a, i * s, p);

            for (int j = i * s; ; ++ j) {

                if (v == b) return j;

                v = 1ll * v * a % p;

            }

        }

    }

    return -1;

}

这里我们不想用排序 $ + $ 二分，所以我们直接使用 set 偷懒

二、加法原理和乘法原理

加法原理

同一阶段内算方案数，用加法原理加起来

乘法原理

不同阶段组合，用乘法原理乘起来

三、排列和组合

排列

三个人找两个人排成一列，有 $ 6 $ 种方案：

  1. $ \text {1 2} $

  2. $ \text {1 3} $

  3. $ \text {2 1} $

  4. $ \text {2 3} $

  5. $ \text {3 1} $

  6. $ \text {3 2} $

这种计算分不同的情况，每种情况选择了以后，下一次选择能选择的数目有少了一种，所以计算公式如下：

$ P(n, m) = n \times (n - 1) \times (n - 2) \times \dots \times (n - m + 1) $

我们把以上式子补全一下，从 $ (n - m + 1) $ 接着往下乘，乘到 $ 1 $，然后把多乘的再除一下，然后凑出了两个阶乘，化简如下：

$ P(n, m) = \frac{n!}{(n - m)!} $

组合

组合的话就是不考虑顺序，比如说三个人选两个人，不考虑顺序，方案数如下：

  1. $ \text{1 2} $

  2. $ \text{1 3} $

  3. $ \text{2 3} $

这样的话我们还是考虑先写出排列的公式 $ \frac{n!}{(n - m)!} $，然后考虑顺序，如果选出的 $ m $ 个人随便站，第一个人有 $ m $ 个位置可以站，第二个人有 $ m - 1 $ 个位置可以站，这样的话总方案数是 $ m! $，然后把多余的方案数除掉就行 $ C(n, m) = \frac{n!}{m!(n - m)!} $

关于组合的一些性质

  1. $ C(n, 0) = 1 $

这个比较好理解，什么都不选的方案数是 $ 1 $，那就是什么都不选

  1. $ C(n, n) = 1 $

这个比较也好理解，那就是全选的方案数也是 $ 1 $

  1. $ C(n, m) = C(n, n - m) $

第一个式子可以理解为选出 $ n - m $ 个丢掉，其实和第二个式子是等价的

  1. $ C(n, m) = C(n - 1, m - 1) + C(n - 1, m) $

这个叫做组合数的递推式

可以使用 01 背包的思路理解，这里我们考虑当前的这个物品选还是不选，如果是选的话，就是在之前的 $ n - 1 $ 个物品里面选好 $ m - 1 $ 个，然后把当前物品选上，如果不选的话，就是在之前的 $ n - 1 $ 个物品里面选好 $ m $ 个，然后这个物品不选，这样就好理解了

也可以带进去算算：

$ C(n - 1, m - 1) + C(n - 1, m) = \frac{(n - 1)!}{(m - 1)!(n - m)!} + \frac{(n - 1)!}{m!(n - 1 - m)!} $

然后通分一下就是：

$ \frac{(n - 1)!m}{m!(n - m)!} + \frac{(n - 1)!(n - m)}{m!(n - m)!} $

相加：

$ \frac{(n - 1)!m + (n - 1)!(n - m)}{m!(n - m)!} $

提公因数：

$ \frac{(n - 1)!(n - m + m)}{m!(n - m)!} $

化简：

$ \frac{(n - 1)!n}{m!(n - m)!} = \frac{n!}{m!(n - m)!} = C(n, m) $

算了一大顿，终于得证啦

  1. 和杨辉三角形（田田）的关系

这里我们发现，$ C(n, m) $ 的递推公式和杨辉三角形的公式一模一样，然后对应一下就会发现杨辉三角形的第 $ i $ 行第 $ j $ 列就是 $ C(i, j) $

  1. $ C(n, 0) + C(n, 1) + \dots + C(n, n - 1) + C(n, n) = 2^n $

放到每个物品去理解，每个物品有两种情况，要么选，要么不选，由于以上式子涵盖所有情况，我们可以直接把总情况算出来，即 $ 2^n $

  1. $ C(n, 0) - C(n, 1) + \dots - C(n, n - 1) + C(n, n) $

我们发现，减去的是选奇数个东西的方案数，加上的是选偶数个东西的方案数

考虑证明选奇数方案数和选偶数方案数相等

image

看上图，我们发现如果要计算下面的一行，我们考虑每个点对应的上一行的节点，这用到了性质 $ 4 $

第一个点对应上一行的节点 $ 1 $，然后第二个节点减去了节点 $ 1 $ 和节点 $ 2 $，第三个点加上了节点 $ 2 $ 和节点 $ 3 $，第四个节点减去了节点 $ 3 $ 和节点 $ 4 \dots $

然后就两两抵消了

四、二项式定理

先看一张图：

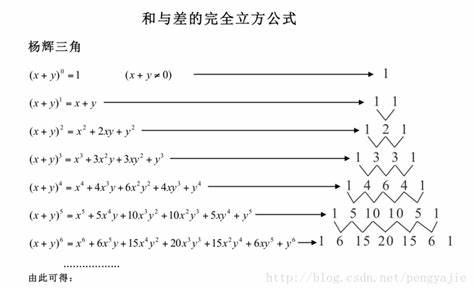
image

是不是发现规律了？二项式拆开的系数和杨辉三角对应，次数加一对应层数，然后我们就得出了公式

$ (x + y)^n = \sum_{i = 0}^{n}C(n, i)x^{n - i}y^i $

五、好玩的例题

例题一

$ n $ 个数，选 $ m $ 个，一个数可以选择多次，求方案数

这种题就比较简单了，首先我们考虑把选出来的排序，即写成不等式：$ 1 \le a_1 < a_2 < \dots < a_m \le n $

然后发现可以重复，那我们把小于改成小于等于不就行了吗： $ 1 \le b_1 \le b_2 \le \dots \le b_m \le n $

然后考虑如何转化为上面的情况，令 $ c_i = b_i + i - 1 $，这样不等式就变成了 $ 1 \le c_1 < c_2 < \dots < c_m \le n + m - 1 $

这里发现解的数量是 $ C(n + m - 1, m) $，由于 $ b, c $ 的解是对应的，所以答案是 $ C(n + m - 1, m) $

例题二（Lucas 定理）

求 $ C(n, m) \bmod p $

代码的模板：

这个我们先看部分分：

$ \text{Subtask 1 } n,m \le 10^{18}, p = 1 $

这个我们直接输出 $ 0 $ 就行

cout << 0 << endl;

$ \text{Subtask 2 } n,m \le 1000 $

这个直接 $ O(n^2) $ 的递推求即可

递推式：$ C(n, m) = C(n - 1, m - 1) + C(n - 1, m) $

int C[1005][1005];

C[1][1] = 1;

for (int i = 1; i <= n; ++ i) {

    C[i][0] = 1;

    for (int j = 1; j <= m; ++ j)

        C[i][j] = C[i - 1][j - 1] + C[i - 1][j] % p;

}

cout << C[n][m] << endl;

$ \text{Subtask 3 } n,m \le 10^6,p $ 为素数

直接求出逆元套用组合数公式就可以了，这里由于有阶乘，可以直接求出阶乘的逆元

其实代码藏在 Day2 的笔记里面，这里不写了，可以自行复制

int fac[1000005], invfac[1000005];

fac[0] = fac[1] = 1;

for (int i = 2; i <= n; ++ i) fac[i] = fac[i - 1] * i % p;

invfac[n] = inv (fac[n], p);

for (int i = n - 1; i >= 1; -- i) {

    invfac[i] = invfac[i + 1] * (i + 1) % p;

}

cout << fac[n] * invfac[m] % p * invfac[n - m] % p << endl;

$ \text{Subtask 4 } n \le 10^9, m \le 10^3 $

眼睛不瞎的可以看出来，$ m $ 很小，所以我们猜想这是一个 $ O(m^2) $ 的算法

首先我们把组合数公式拆开，得到 $ C(n, m) = \frac{n!}{m!(n - m)!} = \frac{m \times (m + 1) \times \dots \times n}{m!} = \frac{\prod_{i = 0}^{m - 1} n - i}{m!} $

可以发现，上下的式子的项数都是接近 $ m $ 项，然后我们可以使用 $ O(m^2) $ 的复杂度两两约分就可以得到最简形式，我们在约分的时候需要使用 __gcd(int x, int y)，复杂度是 $ \log $ 的，所以总复杂度是 $ O(m^2\log{m}) $

考虑到分子一定能整除分母（毕竟组合数公式不可能算出来分数是吧，真严谨的证明啊），所以化成最简形式直接算分子就可以了

代码如下：

int up[114514], down[114514];

for (int i = 1; i <= m; ++ i) down[i] = i, up[i] = n - i + 1;

for (int i = 1; i <= m; ++ i) {

    for (int j = 1; j <= m; ++ j) {

        int g = __gcd (up[i], down[j]);

        up[i] /= g, down[j] /= g;

    }

}

int ans = 1;

for (int i = 1; i <= m; ++ i) ans = ans * up[i] % p;

cout << ans << endl;

$ \text{Subtask 5 } n,m \le 10^9, p \le 100 $ 且为素数

这里引入 Lucas 定理：

$ C(n, m) \equiv C(n / p, m / p) \times C(n \bmod p, m \bmod p) (\text{mod p}) $

接着观察式子，我们会发现，这其实就是把 $ n,m $ 按 $ p $ 进制算出来按位取组合数值，比如说 $ n = 514, m = 114, p = 6 $，那么式子如下：

$ C(514, 114) \equiv C(5, 1) \times C(1, 1) \times C(4, 4) (\text{mod 6}) $

然后就求出来了

首先 $ O(p^2) $ 求出来所有的组合数，然后短除法求出 $ n $ 和 $ m $ 就解决了

# include <bits/stdc++.h>

using namespace std;

int n, m, p;

int C[114][514];

int a[1145], b[4514], cnt1, cnt2;

inline int solve () {

    while (n) {

        a[++ cnt1] = n % p;

        n /= p;

    }

    while (m) {

        b[++ cnt2] = m % p;

        m /= p;

    }

    int ans = 1;

    for (int i = 1; i <= cnt1; ++ i) ans = (ans * C[a[i]][b[i]]) % p;

    return ans;

}

signed main () {

    cin >> n >> m >> p;

    C[1][1] = 1;

    for (int i = 1; i <= p; ++ i) {

        C[i][0] = 1;

        for (int j = 1; j <= p; ++ j) {

            C[i][j] = C[i - 1][j - 1] + C[i - 1][j];

            C[i][j] %= p;

        }

    }

    cout << solve () << endl;

    return 0;

}

六、难题

例题一

把 $ x $ 拆成 $ k $ 个不同组合数的和（只要 $ n1,n2 $ 或者 $ m1,m2 $ 不同就算不同），输出任意方案

考虑把 $ x $ 拆成：$ 1 + 1 + \dots + 1 + (n - k + 1) $

然后这样构造：$ C(1, 0) + C(2, 0) + \dots + C(k - 1, 0) + C(n - k + 1, 1) $

完事

代码：

# include <bits/stdc++.h>

using namespace std;

signed main () {

    int n, k;

    cin >> n >> k;

    for (int i = 1; i <= k - 1; ++ i) cout << i << " " << 0 << endl;

    cout << n - k + 1 << " " << 1 << endl;

    return 0;

}

例题二

比较 $ C(n1, m1) $ 和 $ C(n2, m2) $ 的关系

这里我们有 $ \log{(a \times b)} = \log{a} + \log{b}, \log{(a \div b)} = \log{a} - \log{b} $

如果 $ \log{a} < \log{b} $ 那么 $ a < b $

根据以上，我们可以进行计算 $ \log{C(n, m)} $

首先 $ C(n, m) = \frac{n!}{m!(n - m)!} $

所以 $ \log{C(n, m)} = \log{n!} - \log{m!} - \log{(n - m)!} $

然后就行了

求阶乘的 $ \log $ 的话，我们可以考虑到 $ \log{i} = \log{i - 1} + \log{i} $

递推求即可

代码：

# include <bits/stdc++.h>

using namespace std;

int fac[114514];

int n1, n2, m1, m2;

signed main () {

    cin >> n1 >> m1 >> n2 >> m2;

    for (int i = 1; i <= n; ++ i) fac[i] = fac[i - 1] + log (i);

    int c1 = fac[n1] - fac[m1] - fac[n1 - m1], c2 = fac[n2] - fac[m2] - fac[n2 - m2];

    if (c1 > c2) cout << "A > B" << endl;

    else if (c1 < c) cout << "A < B" << endl;

    else cout << "A = B";

    return 0;

}

例题三

找 $ k $ 个不同的 $ C(a, b) $ 使得和最大，$ 0 \le b \le a \le n $

  1. $ k = 1 $

我们找最大的，直接就是最后一行最中间的就行

  1. $ k = 2 $

第二大的肯定在最大的周围，可能在上一行，或者左右的，有四个位置，比较一下就行了，用例题二比较就行了

  1. $ k $ 很大

这样的话每次找到一个点，我们就把这个点周围的数丢进堆里，然后比较即可

是不是非常简单

代码：

咕咕

例题四 P3746

咕咕

七、抽屉原理

基本原理

基本原理：$ n + 1 $ 个东西放进 $ n $ 个抽屉里，至少有一个抽屉有 $ 2 $ 个东西

简单推广：$ kn + 1 $ 个东西放进 $ n $ 个抽屉里，至少有一个抽屉有 $ k + 1 $ 个东西

POJ 3370

在 $ n $ 个数中选出任意多个数使其为 $ p $ 的倍数

设数组 $ sum $ 为数组 $ a $ 的前缀和，根据对 $ p $ 取模所得结果分类放进抽屉，如果 $ n > p $ 根据抽屉原理一定有解，然后我们把同一个抽屉里的两个前缀和相减得到区间即可

代码：

# include <bits/stdc++.h>

using namespace std;

int T;

int n, c;

int a[114514], sum[114514];

vector < int > box[10005];

inline void solve () ;

signed main () {

    cin >> T;

    while (T --) {

        solve ();

    }

inline void solve () {

    cin >> n >> c;

    for (int i = 0; i < c; ++ i) box[i].clear ();

    for (int i = 1; i <= n; ++ i) cin >> a[i];

    for (int i = 1; i <= n; ++ i) sum[i] = (sum[i - 1] + a[i] % c) % c, box[sum[i] % c].push_back (i);

    for (int i = 0; i < c; ++ i) {

        if (box[i].size () > 1) {

            int l = box[i][0], r = box[i][1];

            for (int i = l + 1;i <= r;++ i) cout << a[i] << " ";

            break;

        }

    }

    cout << endl;

}

P2218

咕咕

八、容斥原理

集合相关

集合的定义是：一般地，研究对象统称为元素，一些元素组成的总体叫集合，也简称集

设 $ A $ 是一个集合

  1. 如果 $ a $ 是集合 $ A $ 的元素，就说 $ a $ 属于 $ A $，记作 $ a \in A $

  2. 如果 $ a $ 不是集合 $ A $ 的元素，就说 $ a $ 不属于 $ A $，记作 $ a \notin A $

没有元素的集合叫做空集，记作 $ \emptyset $

当一个集合 $ A $ 的所有元素都在另一个集合 $ B $ 里，称集合 $ A $ 是集合 $ B $ 的子集，记作 $ A \subseteq B $

$ A \cap B \(：\) A $ 和 $ b $ 的交集

$ A \cup B \(：\) A $ 和 $ b $ 的并集

$ | A | $ 集合 $ A $ 的大小

真·容斥

根据上面的定理，我们就可以得到 $ | A \cup B | = | A | + | B | - | A \cap B | $

同理：$ | A \cup B \cup C | = | A | + | B | + | C | - | A \cap B | - | A \cap C | - | B \cap C | + | A \cap B \cap C | $

我们考虑 $ n $ 个集合，那么式子就会变成 $ \sum_{B \in (A_1,A_2,\dots,A_n)} (-1)^{| B | + 1} \times | \cap_{A_i \in B} A_i | $

简单的问题

然后考虑两个简单的问题

  1. $ n $ 个人坐成一排的方案数 $ n! $

证明：

每个位置考虑方案数，第一个位置可以选择 $ n $ 个人，第二个位置就可以选择 $ n - 1 $ 个人 $ \cdots $

考虑使用乘法原理得到 $ n! $

  1. $ n $ 个人坐成一圈且旋转算相同方案的方案数 $ (n - 1)! $

证明:

考虑延续上面的结果 $ n! $，每种方案可以被旋转 $ n $ 次，除以 $ n $ 即可

posted @ 2023-05-01 09:06  __Tzf  阅读(60)  评论(3)    收藏  举报