bzoj 1911 特别行动队

 

题意：将 n 个人分组，分组后，一个组的战斗力等于 a*sum*sum + b*sum + c，怎么分组使得战斗力和最大。

分析：

第一次自己从头到尾推出来的斜率DP。

状态定义 d[i] ： 前 i 个人分组得到的最优值。

状态转移 d[i] =  max (  d[j]  + a*(sum[i] - sum[j])^2 +b*(sum[i] - sum[j])  +c   )

显然是O(n^2)

 

假设 k < j < i ； j 决策点更优。

 

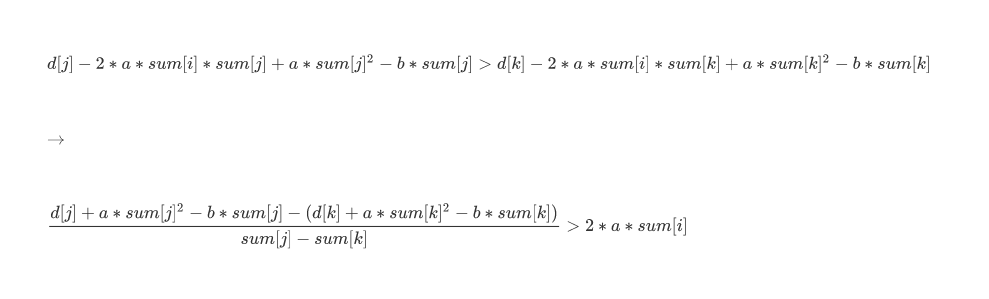
 这个斜率公式比较复杂了，其实就是将分子，分母转为 与 j 和 k 有关的斜率式子，另一边不能有关于 j 和 k 。

有了这个斜率公式，接下来就是分析斜率递增还是递减了。

 

假设3个决策点 k < j < i

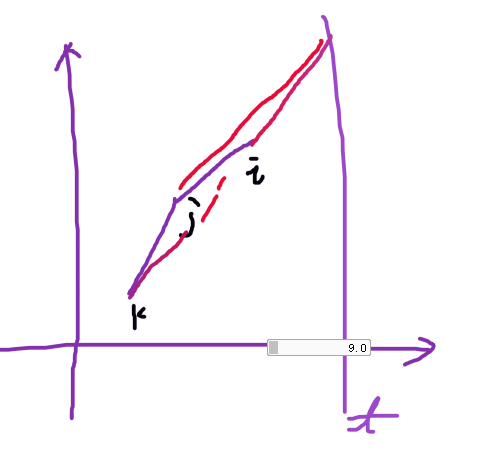
显然 凸多边形，j 点不是最优点，不可能存在凸点。

然后就是根据多边形的性质，相切之前怎么样，加入之后删点等... ...

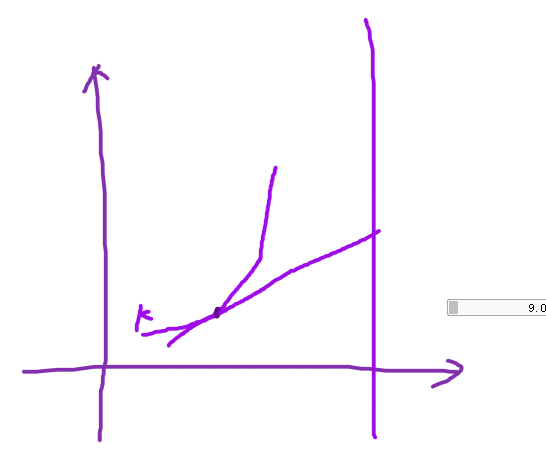
#include<bits/stdc++.h>

using namespace std;
const int maxn = 1e6+5;

int n;
long long a,b,c;
long long x;
long long sum[maxn];
long long d[maxn];
double slope(int i,int j)
{
    double up = d[i]-d[j]+a*(sum[i]*sum[i]-sum[j]*sum[j])+b*(sum[j]-sum[i]);
    double down = 2*a*(sum[i]-sum[j]);
    return up/down;
}
int l,r,q[maxn];

int main()
{
    scanf("%d",&n);
    scanf("%lld%lld%lld",&a,&b,&c);
    long long x;
    for(int i = 1; i <= n; i++) {

        scanf("%lld",&x);
        sum[i] = sum[i-1] + x;
    }

    for(int i=1;i<=n;i++)
    {
        while(l<r&&slope(q[l],q[l+1])<sum[i])l++;
        int now = q[l];
        d[i]=d[now]+a*(sum[i]-sum[now])*(sum[i]-sum[now])+b*(sum[i]-sum[now])+c;
        while(l<r&&slope(q[r-1],q[r])>slope(q[r],i))r--;
        q[++r]=i;
    }
    printf("%lld\n",d[n]);

    return 0;
}