【学习笔记】AC 自动机

前情提要

~~笔者学了三年 kmp 依旧是没有学会。~~

但是 AC 自动机可扔掉 kmp 来学。

简介：AC 自动机

前置需要了解一些字符串相关定义。

它并不像字面意思一样是可以让你的代码轻松得到 Accepted 的算法，全称是 Aho-Corasick Automaton，也就是说 AC 只是两个人名的缩写，Automaton 则是自动机的意思。

自动机是什么？

OI 里面大多数都是指有限状态自动机。

（以下为笔者自己的理解）。

说白了就是你有给定的两个集合 \(S,T\)，对于集合中的元素有限制条件 \(p\)，就比如数据范围的限制或者只能是某个字符集中的字符等等，然后将集合 \(S\) 作为基准集合，集合 \(T\) 作为待配对集合，同时我们有一个函数 \(f_{x,y}\)，\(x\) 表示当前配对到集合 \(S\) 的某一位置，\(y\) 表示集合 \(S\) 这个位置的元素，如果说 \(T\) 满足这个函数的限制，比如判定是子串或者子序列之类的，那就可配对然后跳到下一个状态。

（笔者理解能力约等于零）。

好吧其实整出来类似于一个有向图，\(S\) 就是初始这个图的样子，\(f_{x,y}\) 为边，如果 \(T\) 中匹配的话就可以通过，否则不行，这样子去匹配图。

AC 自动机，它是拿来匹配字符串子串的自动机，一般是会有一个初始模式串集合，然后会有文本串匹配或者其它方式的问题。

AC 自动机的主体是一棵 Trie 树，我们将模式串集合放到 Trie 上，如图：

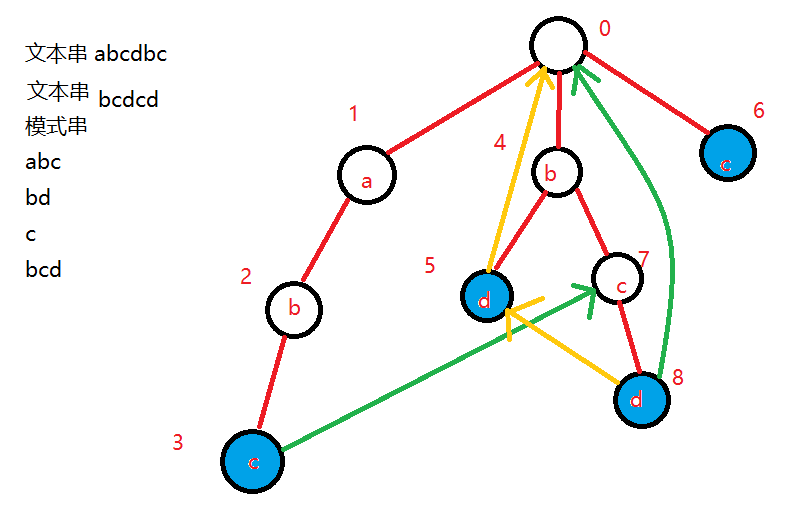
蓝色为模式串结尾。

假设现在我们要匹配第一个文本串 abcdbc，首先我们会找到 \(3\) 号节点，但是之后就没有了，这时我们需要失配指针 \(fail\)，具体的，\(fail\) 指针是在下一字符不匹配或没有子节点的情况下跳到另一个节点继续匹配的一条有向边，其实它的原理是一个 trick：如果我们想要找子串，考虑枚举前缀然后截取前缀的后缀，也就是说 \(fail\) 指针指向节点所代表的的字符串是当前节点所代表的字符串的后缀，且指向的节点在同类型节点中深度最深（不重不漏从深往浅匹配子串），如图我们会找到 \(7\) 号节点，然后匹配到 \(8\) 号节点发现又无法匹配了，且没有 \(fail\) 指针可指向的非根节点，此时我们的 \(fail\) 就指向根重新开始继续匹配。

第二个文本串 bcdbd 也同理，可以自行按照图理解。

P3808 AC 自动机（简单版）

这是最简单的一版。

考虑根据刚才的做法，我们在找到无法继续匹配的节点后跳 \(fail\) 指针继续匹配。

如何求 \(fail\) 指针呢？

我们用 bfs 来求，对于根节点的儿子其 \(fail\) 必定指向根，然后把它们入队，之后我们找到队中节点的儿子，这时我推导以下性质，就以刚才的图为例，假设 \(3\) 号节点下还有一个儿子 \(9\) 号节点字符为 d，如果说我们匹配到 \(3\) 号节点匹配不了了，那么 \(fail_3\) 会指向 \(7\) 号节点，同理 \(9\) 号节点匹配不了了 \(fail_9\) 会指向 \(8\) 号节点，多试几组数据就可以发现一个节点的儿子的 \(fail\) 指针就是这个节点的 \(fail\) 指针的儿子，是不是比较绕？变成式子就是 \(fail_{son_i} = son_{fail_i}\)。

当然如果当前节点没有儿子的话就令其儿子为其 \(fail\) 指针的儿子。

考虑我们怎么统计答案，因为是跳 \(fail\) 指针所以我们只会找到字符串尾的节点，那么我们统计有多少模式串在该节点结尾即可。

这道题简单的原因是数据比较水所以暴力跳 \(fail\) 可过。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e6 + 10;
int N, cnt;
string S, T;

struct AcNode {
	int son[26], fail, tot;
	#define son(rt,x) Ac[rt].son[x]
	#define fail(rt) Ac[rt].fail
} Ac[MAXN];

inline void InsertString (string str) {
	int len = str.length(), now = 0;
	for (int i = 0; i < len; i ++) {
		int ch = str[i] - 'a';
		if (!son(now, ch)) 
			son(now, ch) = ++cnt;
		now = son(now, ch);
	}
	return ++Ac[now].tot, void();
}

inline void getFailPointer() {
	queue<int> q;
	for (int i = 0; i < 26; i ++) {
		if (!son(0, i)) continue;
		fail(son(0, i)) = 0, q.emplace (son(0, i));
	}
	while (!q.empty()) {
		int now = q.front(); q.pop();
		for (int i = 0; i < 26; i ++) {
			if (son(now, i)) fail(son(now, i)) = son(fail(now), i), q.emplace (son(now, i));
			else son(now, i) = son(fail(now), i);
		}
	}
	return;
}

inline int query (string str) {
	int len = str.length(), now = 0, res = 0;
	for (int i = 0; i < len; i ++) {
		int ch = str[i] - 'a';
		now = son(now, ch);
		for (int j = now; j && ~Ac[j].tot; j = fail(now))
			res += Ac[j].tot, Ac[j].tot = -1;
	}
	return res;
}

signed main() {
	ios_base::sync_with_stdio (false);
	cin.tie (nullptr), cout.tie (nullptr);
	cin >> N, cnt = fail(0) = 9;
	for (int i = 1; i <= N; i ++)
		cin >> S, InsertString(S);
	cin >> T, getFailPointer();
	cout << query(T) << "\n";
	return 0;
}

P5357 【模板】AC 自动机

不保证任意两个模式串不相同啊，用桶去个重就行。

此时需要打表找下规律或者深度思考一下你会发现，我们暴力跳 \(fail\) 会形成一条链，假设链为 \(\{x_1,x_2,\dots x_k\}\)，那么我们第一次会从 \(x_1\) 开始跳直到 \(x_k\)，如果我们有幸又找到 \(x_2\)，则又会从 \(x_2\) 开始跳到 \(x_k\)，这不亏麻了，也就是说我们要优化这个过程。

给每个点打标记，把答案向上更新，最后在链尾处得到答案，这样是可行的。

考虑用拓扑实现，因为 \(fail\) 指针其实就是一条有向边，这样连边跑拓扑就行，对于当前节点结尾的模式串，它的答案就是当前从链头累计上来的答案。

这样我们的复杂度来到了 \(O(\left|S\right| + \left|T\right|)\)，可通过。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 2e5 + 10;
int N, cnt, indeg[MAXN], mp[MAXN], ans[MAXN];
string S, T;

struct AcNode{
	int son[26], end, flag, fail;
	#define son(rt,x) Ac[rt].son[x]
	#define fail(rt) Ac[rt].fail
} Ac[MAXN];

inline void Insert (string str, int pos) {
	int len = str.length(), now = 0;
	for (int i = 0; i < len; i ++) {
		int ch = str[i] - 'a';
		if (!son(now, ch))
			son(now, ch) = ++cnt;
		now = son(now, ch);
	}
	if (!Ac[now].end)
		Ac[now].end = pos;
	mp[pos] = Ac[now].end;
}

inline void getFailPointer() {
	queue<int> q;
	for (int i = 0; i < 26; i ++) {
		if (!son(0, i)) continue;
		fail(son(0, i)) = 0, q.emplace (son(0, i));
	}
	while (!q.empty()) {
		int now = q.front(); q.pop();
		for (int i = 0; i < 26; i ++) {
			if (!son(now, i)) {
				son(now, i) = son(fail(now), i);
			} else {
				fail(son(now, i)) = son(fail(now), i);
				indeg[fail(son(now, i))] ++, q.emplace (son(now, i));
			}
		}
	}
	return;
}

inline void query (string str) {
	int len = str.length(), now = 0;
	for (int i = 0; i < len; i ++) {
		int ch = str[i] - 'a';
		now = son(now, ch), Ac[now].flag ++;
	}
	return;
}

inline void tpSort() {
	queue<int> q;
	for (int i = 1; i <= cnt; i ++) if (!indeg[i]) q.emplace(i);
	while (!q.empty()) {
		int now = q.front(); q.pop();
		ans[Ac[now].end] = Ac[now].flag;
		int nxt = fail(now);
		Ac[nxt].flag += Ac[now].flag;
		if (!--indeg[nxt]) q.emplace(nxt);
	}
	return;
}

signed main() {
	ios_base::sync_with_stdio (false);
	cin.tie (nullptr), cout.tie (nullptr);
	cin >> N, fail(0) = cnt = 0;
	for (int i = 1; i <= N; i ++)
		cin >> S, Insert (S, i);
	getFailPointer();
	cin >> T, query(T);
	tpSort();
	for (int i = 1; i <= N; i ++)
		cout << ans[mp[i]] << "\n";
	return 0;
}

现在你应该学会了基础的 AC 自动机，接下来是例题的讲解。

P2414 [NOI2011] 阿狸的打字机

首先把所有串拆出来建自动机，我们暴力跳 \(fail\) 找 \(x\) 串的末尾，但是这样时间复杂度飞起。

你想啊，我们在跳 \(fail\) 对吧，对于每个点有且仅有一个 \(fail\)，那么这样一来就是一棵树，每次查询就是从 \(y\) 串的某个节点向上跳到 \(x\) 末节点，反过来就是往子树跳能到达多少个 \(y\) 串的节点，感觉很可做啊，考虑求子树和。

首先依旧是一个性质：子树内 \(dfn\) 连续，那么我们可以对于 \(y\) 串的每个点打上 \(1\) 的标记，每次就是求 \(x\) 末节点的子树和，这样可以 \(dfn\) 上求连续一段。

你发现这玩意每次把 \(y\) 串的点插入树状数组，对于结束的位置打 \(-1\)，其余打 \(1\)（在 dfs 中实现），那么打了标记的一定是当前询问的串。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e5 + 10;
int M, cnt, len, top, idx, tot, ind;
int cut[MAXN], BIT[MAXN], stk[MAXN], head[MAXN], siz[MAXN], dfn[MAXN], ans[MAXN];
string T;

struct queNode {
	int x, y, id;
	bool operator < (const queNode &s) const { return y != s.y ? y < s.y : id < s.id; }
} que[MAXN];

struct AcNode {
	int son[26], fail;
	#define son(rt,x) Ac[rt].son[x]
	#define fail(rt) Ac[rt].fail
} Ac[MAXN];

struct eNode {
	int to, nxt;
} E[MAXN];

inline void Addedge (int u, int v) { E[idx].to = v, E[idx].nxt = head[u], head[u] = idx++; }

inline void Build_AC() {
	int now = 0;
	for (int i = 0; i < len; i ++) {
		if (T[i] >= 'a' && T[i] <= 'z') {
			int ch = T[i] - 'a';
			if (!son(now, ch))
				son(now, ch) = ++cnt;
			now = son(now, ch), stk[++top] = now;
		} else if (T[i] == 'B') {
			now = stk[--top];
		} else {
			cut[++tot] = now;
		}
	}
	return;
}

inline void getFailPointer() {
	queue<int> q;
	for (int i = 0; i < 26; i ++) {
		if (!son(0, i)) continue;
		fail(son(0, i)) = 0;
		q.emplace (son(0, i));
		Addedge (0, son(0, i));
	}
	while (!q.empty()) {
		int now = q.front(); q.pop();
		for (int i = 0; i < 26; i ++) {
			if (!son(now, i)) {
				son(now, i) = son(fail(now), i);
			} else {
				fail(son(now, i)) = son(fail(now), i);
				q.emplace (son(now, i)), Addedge (fail(son(now, i)), son(now, i));
			}
		}
	}
	return;
}

inline int lowbit (int x) { return x & (-x); }

inline void addon (int p, int k) { for (; p <= cnt + 1; p += lowbit(p)) BIT[p] += k; }

inline int askon (int p) {
	int res = 0;
	for (; p > 0; p -= lowbit(p))
		res += BIT[p];
	return res;
}

void dfs (int u) {
	dfn[u] = ++ind, siz[u] = 1;
	for (int i = head[u]; ~i; i = E[i].nxt) 
		dfs (E[i].to), siz[u] += siz[E[i].to];
}

signed main() {
	ios_base::sync_with_stdio (false);
	cin.tie (nullptr), cout.tie (nullptr);
	cin >> T >> M, len = T.size();
	memset (head, -1, sizeof (head));
	for (int i = 1; i <= M; i ++) 
		cin >> que[i].x >> que[i].y, que[i].id = i;
	sort (que + 1, que + M + 1);
	Build_AC(), getFailPointer(), dfs(0);
	int pt = 0, now = 0, top = 0, up = 0;
	for (int i = 1; i <= M; i ++) {
		for (; up < que[i].y; pt ++) {
			if (T[pt] >= 'a' && T[pt] <= 'z') {
				int ch = T[pt] - 'a';
				now = son(now, ch);
				stk[++top] = now, addon (dfn[now], 1);
			} else if (T[pt] == 'B') {
				addon (dfn[now], -1), now = stk[--top];
			} else {
				up ++;
			}
		}
		int t = cut[que[i].x];
		ans[que[i].id] = askon (dfn[t] + siz[t] - 1) - askon (dfn[t] - 1);
	}
	for (int i = 1; i <= M; i ++)
		cout << ans[i] << "\n";
	return 0;
}

CF696D Legen...

看到子串出现次数，首先会想到建 AC 自动机，这样我们就处理掉了子串出现次数的问题。

但是它带了一个权值 \(val_i\)，考虑 dp，记 \(f_{i,j}\) 表示当前构造到了长度 \(i\)，在自动机上以 \(j\) 节点结尾的最大价值，记录每个串的结尾 \(end\)，直接 \(end \leftarrow end + val_i\) 就可以更方便得到一个子串的权值，只需要在 \(fail\) 树上子树和。

那么我们肯定是从根往子节点一路跳，就有：

\[f_{i+1,son_{j,x}} \leftarrow \max\{f_{i,j} + val_{son_{j,x}}\} \]

但是你看到 \(l\leq 10^{14}\)，这样转移瞬间爆炸。

诶！当我们转移的时候有且仅有 \(i \to i + 1\)，那么就可以用矩乘快速幂来优化（其实转移跟遍历图差不多，从上一个状态走到下一个）。

为符合转移的运算我们把矩乘重定义为加法然后取 \(\max\)，初始矩阵 \(mat_{i,son_{i,j}} = end_{son_{i,j}}\)，想要的答案是 \(\max\limits_{i=0}^{N}{mat_{0,i}}\)。

#include <bits/stdc++.h>
#define int long long
#define fail(now) Amt[now].fail
#define end(now) Amt[now].end
#define son(now,x) Amt[now].son[x]

using namespace std;
const int MAXN = 210;
const int MAXS = 200010;

int N, M, cnt, ans;
int val[MAXN];
string Style;

struct Amton {
	int son[26];
	int fail, end;
} Amt[MAXS];

struct Matt {
	int mat[MAXN][MAXN];
	
	Matt() { memset (mat, -0x3f, sizeof(mat)); }
	Matt operator * (const Matt &s) const {
		Matt res = Matt();
		for (int k = 0; k <= cnt; k ++) {
			for (int i = 0; i <= cnt; i ++) {
				for (int j = 0; j <= cnt; j ++)
					res.mat[i][j] = max (res.mat[i][j], mat[i][k] + s.mat[k][j]);
			}
		}
		return res;
	}
} base, final;

Matt binpow (Matt x, int p) {
	Matt res = x;
	for (--p; p; p >>= 1) {
		if (p & 1)
			res = res * x;
		x = x * x;
	}
	return res;
}

inline void InsertString (int val) {
	int now = 0, len = Style.length();
	for (int i = 0; i < len; i ++) {
		int chVal = Style[i] - 'a';
		if (!son(now, chVal))
			son(now, chVal) = ++cnt;
		now = son(now, chVal);
	}
	end(now) += val;
}

inline void GetFailPointer() {
	queue<int> q;
	for (int i = 0; i < 26; i ++) {
		if (son(0, i))
			q.emplace (son(0, i));
	}
	while (!q.empty()) {
		int now = q.front(); q.pop();
		end(now) += end(fail(now));
		for (int i = 0; i < 26; i ++) {
			if (!son(now, i))
				son(now, i) = son(fail(now), i);
			else {
				fail(son(now, i)) = son(fail(now), i);
				q.emplace (son(now, i));
			}
		}
	}
}

signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> N >> M, base = Matt();
    for (int i = 1; i <= N; i ++) cin >> val[i];
    for (int i = 1; i <= N; i ++) cin >> Style, InsertString(val[i]);
    GetFailPointer();
    for (int i = 0; i <= cnt; i ++) {
    	for (int j = 0; j < 26; j ++)
    		base.mat[i][son(i, j)] = end(son(i, j));
	}
	final = binpow (base, M);
    ans = -0x7f7f7f7f7f7f;
    for (int i = 0; i <= cnt; i ++)
    	ans = max (ans, final.mat[0][i]);
    cout << ans << '\n';
    return 0;
}

CF163E e-Government

看来是比较典的 AC 自动机的题目。

首先我们摸出一个 trick：求子串可以枚举前缀然后考虑这段前缀的后缀。

那么我们对集合 \(\{T\}\) 建 AC 自动机，那么当我们从根往下走的时候就是在枚举前缀（因为是 trie 树），然后处理 \(fail\) 指针，根据 \(fail\) 的含义：指向当前前缀的最长后缀的尾，我们可以通过跳 \(fail\) 得到这段前缀的后缀，每个点都有且仅有一个 \(fail\) 指针，那么从 \(fail_u \to u\) 建边得到的就是一棵外向树（有向且从根指向叶子），原本我们想要的是从 \(u\) 跳 \(fail_u\) 假设最后跳到 \(v\)，那么在新建出来的树上 \(v\) 在 \(u\) 子树内且从 \(fail_u\) 到 \(u\) 子树内任意结点都是一种可行匹配，那么这就是个子树和问题。

但是这道题带删带修，其实再摸出一个 trick：子树内 dfn 连续，所以可以在 dfn 上子树加一或者减一然后上传区间和，暴力单点查统计，线段树或者树状数组维护都可。

Code

#include <bits/stdc++.h>
//#define int long long
#define son(rt,x) Amt[rt].son[x]
#define fail(rt) Amt[rt].fail
#define lson(rt) (rt << 1)
#define rson(rt) (rt << 1 | 1)
#define len(rt) (Sgt[rt].r - Sgt[rt].l + 1)

using namespace std;
const int MAXN = 1e6 + 10;

int N, K, cnt, ind, idx;
int tail[MAXN], low[MAXN], dfn[MAXN], head[MAXN];
bool tag[MAXN];
string Style, Text;

struct Graphon {
	int to, nxt;
} E[MAXN];

struct AutoMaton {
	int son[26];
	int fail;
} Amt[MAXN];

struct Sgton {
	int l, r, sum, lazy;
} Sgt[MAXN << 2];

inline void Addedge (int u, int v) { E[idx].to = v, E[idx].nxt = head[u], head[u] = idx++; }

inline void InsertString (int ID) {
	int len = Style.length(), now = 0;
	for (int i = 0; i < len; i ++) {
		int chVal = Style[i] - 'a';
		if (!son(now, chVal))
			son(now, chVal) = ++cnt;
		now = son(now, chVal);
	}
	tail[ID] = now;
}

inline void GetFailPointer() {
	queue<int> q;
	for (int i = 0; i < 26; i ++) {
		if (son(0, i)) {
			q.emplace(son(0, i));
			Addedge (0, son(0, i));
		}
	}
	while (!q.empty()) {
		int now = q.front(); q.pop();
		for (int i = 0; i < 26; i ++) {
			if (!son(now, i))
				son(now, i) = son(fail(now), i);
			else {
				fail(son(now, i)) = son(fail(now), i);
				q.emplace (son(now, i));
				Addedge (fail(son(now, i)), son(now, i));
			}
		}
	}
}

void dfs (int from) {
	dfn[from] = ++ind;
	for (int i = head[from]; ~i; i = E[i].nxt) dfs (E[i].to);
	low[from] = ind;
}

void Build (int l, int r, int rt) {
	Sgt[rt].l = l, Sgt[rt].r = r;
	if (l == r) return;
	int mid = (l + r) >> 1;
	Build (l, mid, lson(rt));
	Build (mid + 1, r, rson(rt));
}

inline void pushdown (int rt) {
	if (Sgt[rt].lazy) {
		Sgt[lson(rt)].lazy += Sgt[rt].lazy;
		Sgt[rson(rt)].lazy += Sgt[rt].lazy;
		Sgt[lson(rt)].sum += len(lson(rt)) * Sgt[rt].lazy;
		Sgt[rson(rt)].sum += len(rson(rt)) * Sgt[rt].lazy;
		Sgt[rt].lazy = 0;
	}
}

void Modify (int ql, int qr, int rt, int val) {
	int l = Sgt[rt].l, r = Sgt[rt].r;
	if (ql <= l && qr >= r) {
		Sgt[rt].lazy += val;
		Sgt[rt].sum += len(rt) * val;
		return;
	}
	int mid = (l + r) >> 1;
	pushdown(rt);
	if (ql <= mid)
		Modify (ql, qr, lson(rt), val);
	if (qr > mid)
		Modify (ql, qr, rson(rt), val);
	Sgt[rt].sum = Sgt[lson(rt)].sum + Sgt[rson(rt)].sum;
}

int query (int ql, int qr, int rt) {
	int l = Sgt[rt].l, r = Sgt[rt].r;
	if (ql <= l && qr >= r)
		return Sgt[rt].sum;
	int mid = (l + r) >> 1, res = 0;
	pushdown(rt);
	if (ql <= mid)
		res += query (ql, qr, lson(rt));
	if (qr > mid)
		res += query (ql, qr, rson(rt));
	return res;
}

inline int queryAns (string str) {
	int len = str.length(), now = 0, res = 0;
	for (int i = 1; i < len; i ++) {
		int chVal = str[i] - 'a';
		now = son(now, chVal);
		res += query (dfn[now], dfn[now], 1);
	}
	return res;
}

inline int chgStr (string str) {
	int len = str.length(), res = 0;
	for (int i = 1; i < len; i ++)
		res = res * 10 + str[i] - '0';
	return res;
}

signed main() {
	ios_base::sync_with_stdio (false);
	cin.tie (nullptr), cout.tie (nullptr);
	cin >> N >> K, cnt = ind = idx = 0;
	memset (head, -1, sizeof head);
	for (int i = 1; i <= K; i ++) 
		cin >> Style, InsertString(i);
	GetFailPointer(), dfs(0), Build (1, ind, 1);
	for (int i = 1; i <= K; i ++)
		tag[i] = true, Modify (dfn[tail[i]], low[tail[i]], 1, 1);
	for (int i = 1; i <= N; i ++) {
		cin >> Text;
		if (Text[0] == '+') {
			int strVal = chgStr(Text);
//			cout << strVal << "\n";
			if (!tag[strVal])
				tag[strVal] = true, Modify (dfn[tail[strVal]], low[tail[strVal]], 1, 1);
		} else if (Text[0] == '-') {
			int strVal = chgStr(Text);
//			cout << strVal << "\n";
			if (tag[strVal])
				tag[strVal] = false, Modify (dfn[tail[strVal]], low[tail[strVal]], 1, -1);
		} else {
			cout << queryAns(Text) << "\n";
		}
	}
	return 0;
}

总结一下

AC 自动机经常会结合 dp、树形数据结构、图论之类的一起考察，综合性很强。

使用 AC 自动机类似套公式，理解原理可以更好的灵活变通去运用。

题目

CF1437G Death DBMS

综合树剖和线段树。

CF86C Genetic engineering

结合了 dp。

P3311 [SDOI2014] 数数

结合数位 dp。

CF1202E You Are Given Some Strings...

乘法原理脑筋急转弯。

posted @ 2025-05-06 20:34 xAlec 阅读(118) 评论(0) 收藏举报

刷新页面返回顶部

Tomori's Blog