动态规划：合唱团问题解析（一）

牛客网网易的校招编程题

题目：有 n 个学生站成一排，每个学生有一个能力值，牛牛想从这 n 个学生中按照顺序选取 k 名学生，要求相邻两个学生的位置编号的差不超过 d，使得这 k 个学生的能力值的乘积最大，你能返回最大的乘积吗？
输入：每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1 <= n <= 50)，表示学生的个数，接下来的一行，包含 n 个整数，按顺序表示每个学生的能力值 ai（-50 <= ai <= 50）。接下来的一行包含两个整数，k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出：输出一行表示最大的乘积。

因为本人刚学动态规划，所以我先把问题简化后先用递归方式求解，再改进为记忆化搜索，然后用动态规划解决问题，最后求解原问题。
简化后的问题：从 n 个自然数中选取 k 个数，使得这 k 个数的乘积最大。

递归求解

先尝试用递归的方式自上而下的解决，定义状态函数为 F(start, k)，start 为自然数数组索引的起点，k 为要取的数的数量，返回从 start 到数组结束位置中取得的 k 个数的乘积的最大值。假设自然数组为 (X₀, X₁ ,X₂, …, X_n-1) 共 n 个数，我们最终要求的就是 F(0, k)。假设我们选取其中一个数为必选的数，可以得出如下的递归树去解释该问题。

 

 

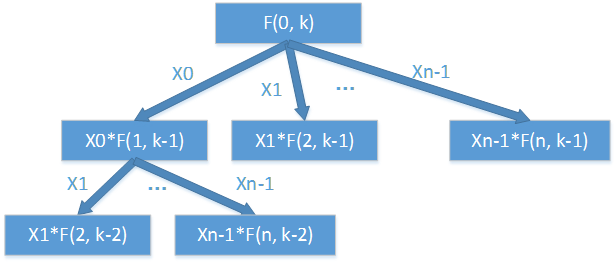
递归的终止条件为当 start >= n 的时候，这时 start 索引已经越界，所以直接返回数字 1 乘以被选取的数字，就相当于返回数组最后一个数字 X_n-1; 同时，当最后 k <= 0 的时候，说明这时无可选取的数字，也就是返回数字 1。基于以上条件，当存在选取超过一定范围内的 k 个数时，会返回范围内所有数字的乘积。实现的代码如下所示：

long long recursive(int a[], int index, int n, int k) {
    if (k <= 0 || index >= n)
        return 1;

    long long result = 0;
    for (int i=index; i < n; i++)
         result = max(result, a[i] * recursive(a, i+1, n, k-1));
    return result;
}

long long result(int a[], int n, int k){
    return recursive(a, 0, n, k);
}

记忆化搜索

因为递归在处理更大规模的数据时运行效率是很低的，存在大量的重复运算，所以我们可以用记忆化搜索的方式去优化递归的方法。因为每个状态依赖于两个变量的变化，所以需要一个二维的数组去存储已经计算过的值。实现的代码如下所示：

vector<vector<long long>> memo;
long long memoSearch(int a[], int index, int n, int k) {
    if (k <= 0 || index >= n)
        return 1;
    if (memo[index][k] != -1)
        return memo[index][k];

    long long result = 0;
    for (int i = index; i < n; i++)
        result = max(result, a[i] * memoSearch(a, i+1, n, k-1));
    memo[index][k] = result;
    return result;
}
 
long long result(int a[], int n, int k){
    memo = vector<vector<long long>>(n, vector<long long>(k+1, -1));
    return memoSearch(a, 0, n, k);
}

动态规划

通过上面递归的分析，我们知道该问题是要求一个最优的解，当自顶向下的分析问题时，我们发现该问题是存在最优子问题的，同时这些子问题可能被重复的计算，所以我们可以用动态规划的方法去自底向上的解决问题，提高计算效率。

我们从最基本的一个子问题 F(start, 1) 开始分析，F(start, 1)=max(X_start*F(1, 0), X_start+1*F(2, 0), …, X_n-1*F(n, 0))。因为假设 k=0 时返回数字 1，所以可得 F(start, 1)=max(X_start, X_start+1, …, X_n-1)。所以当 k = 1 时，我们保留原来所有数组的值，而当 k = 2 时，从头遍历数组，在位置 (start, 2) 上存储 X_start*F(start+1, 1)。所以在编程实现时需要三个 for 循环，第一重循环以 k 计数，第二重以自然数组下标 n 计数，第三重循环取该下标 n 后被存储的数，循环内计算该下标的自然数与存储的数的最大值的积。当计算完最后一列 k 时，最后一列 k 中的最大值就是我们要求的问题的最优解。实现的代码如下所示：

vector<vector<long long>> memo;
long long dpAlgorithm(int a[], int n, int k) {
    memo = vector<vector<long long>>(n, vector<long long>(k+1, -1));
    long long result = 0;
    for (int j = 1; j < k+1; j++) {
        for (int i = 0; i < n; i++) {
            if (j == 1) {
                memo[i][j] = a[i];
            }
            else {
                long long temp = 0;
                for (int index = i + 1; index < n; index++) {
                    temp = max(temp, memo[index][j - 1]);
                    memo[i][j] = temp * a[i];
                }
            }
            if (j == k) result = max(result, memo[i][j]);
        }
    }
    return result;
}

动规算法优化

要实现前面所述的动态规划算法，我们需要一个 n * (k + 1) 的二维矩阵去存储已经计算出的最优值，当 n 和 k 的值很大的时候，就需要更多额外的空间去求解。而实际上我们可以进一步的优化这个空间复杂度。因为在这个问题中，当我们选取一个固定的值时，我们是从其之后存储的最大值与该固定的值相乘，所以之前被存储的值事实上是可以被覆盖的。所以我们只需要一个一维的长度为n的矩阵去实现该算法。实现的代码如下所示：

vector<vector<long long>> memo;
long long dpAlgorithm2(int a[], int n, int k) {
    vector<long long> memo2 = vector<long long>(n, -1);
    long long result = 0;
    for (int j = 1; j < k + 1; j++) {
        for (int i = 0; i < n; i++) {
            if (j == 1) {
                memo2[i] = a[i];
            }
            else {
                for (int index = i + 1; index < n; index++) {
                    memo2[i] = max(memo2[i], a[i] * memo2[index]);
                }
            }
            if (j == k) result = max(result, memo2[i]);
        }
    }
    return result;
}