【笔记】背包 DP

背包 DP

背包 dp

一般是给出一些“物品”，每个物品具有一些价值参数和花费参数，要求在满足花费限制下最大化价值或者方案数。

最简单几种类型以及模型 ：

  • 0/1 背包
  • 完全背包
  • 多重背包

0 / 1 背包

【例题】

【\(Description\)】

给出 \(n\) 个物品，每个物品有 \(V_i\) 的价值和 \(W_i\) 的费用，我们总共有 \(m\) 块钱，求最多能得到多少价值的物品。

\(n,m \leq 10 ^ 3\)

【\(Solution\)】

设 \(dp[i][j]\) 表示前 \(i\) 个物品，用了 \(j\) 的花费得到的最大的价值。

\[dp[i][j]=\max\{dp[i-1][j], dp[i-1][j - w[i]]+v[i]\} \]

复杂度 \(O(N \times M)\)

我们发现这样太耗费空间，或许我们还可以继续优化，可以用滚动数组，因为我们发现每个转移都只由他前面的一种状态来判断，所以可把第一维设置成为 2 来做。

我们再想想，是否可以做到用一维数组来搞定，可以，但是我不会讲 /xyx

【\(Code\)】二维

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int f[1010][1100];
int n,m; 
int v[1100],w[1100];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  m = read(),n = read();
  for(int i = 1;i <= n;i ++) {
    v[i] = read(),w[i] = read();
  }
  for(int i = 1;i <= n;i ++) {
    for(int j = 0;j <= m;j ++) {
      f[i][j] = f[i - 1][j];
      if(j - v[i] >= 0) 
        f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
    }
  }
  printf("%d",f[n][m]);
  return 0;
}

【\(Code\)】滚动数组

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int f[2][1100];
int n,m; 
int v[1100],w[1100];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  m = read(),n = read();
  for(int i = 1;i <= n;i ++) {
    v[i] = read(),w[i] = read();
  }
  for(int i = 1;i <= n;i ++) {
    for(int j = 0;j <= m;j ++) {
      f[i & 1][j] = f[i - 1 & 1][j];
      if(j - v[i] >= 0) 
        f[i & 1][j] = max(f[i & 1][j],f[i - 1 & 1][j - v[i]] + w[i]);
    }
  }
  printf("%d",f[n & 1][m]);
  return 0;
}

【\(Code\)】一维

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int Maxk = 15510;
int f[Maxk]; 
int n,m;
int c[Maxk],w[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  m = read(),n = read();
  for(int i = 1;i <= n;i ++) {
    c[i] = read();w[i] = read();
  }
  for(int i = 1;i <= n;i ++) {
    for(int j = m;j >= c[i];j --) {
      f[j] = max(f[j - c[i]] + w[i],f[j]);
    }
  }
  cout << f[m] << endl;
  return 0;
}

完全背包

每一类物品可以选无限个。

\[dp[i][j]=\max\{dp[i-1][j], dp[i][j-k \times v[i]]+k \times w[i] \ \ | \ \ 1 \leq k \leq \frac{j}{k \times v[i]}\} \]

在这里提一下一个贪心的预处理，对于所有 \(V_i \leq V_j\)，\(W_i \geq W_j\) 的物品 \(j\)，都可以完全扔掉，对于体积相同的物品只需要留下价值最大的物品，对于随机数据这个优化的力度非常大。

代码的 \(v\) 与 \(w\) 的意义相反，代码中的 \(v\) 表示的是价值，\(w\) 表示的是重量。

【\(Code\)】滚动数组

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int Maxk = 1e7 + 10;
int n,m;
int f[2][Maxk];
int v[Maxk],w[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  m = read(),n = read();
  for(int i = 1;i <= n;i ++) {
    v[i] = read(),w[i] = read();
  }
  for(int i = 1;i <= n;i ++) {
    for(int j = 0;j <= m;j ++) {
      f[i & 1][j] = f[i - 1 & 1][j];
      for(int k = 1;(k * v[i]) <= j;k ++) {
        f[i & 1][j] = max(f[i & 1][j],f[i - 1 & 1][j - k * v[i]] + k * w[i]);
      }
    }
  }
  printf("%lld",f[n & 1][m]);
  return 0;
}

【\(Code\)】

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int Maxk = 1e7 + 10;
int n,m;
int f[Maxk];
int v[Maxk],w[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  m = read(),n = read();
  for(int i = 1;i <= n;i ++) {
    v[i] = read(),w[i] = read();
  }
  for(int i = 1;i <= n;i ++) 
    for(int j = v[i];j <= m;j ++) 
      f[j] = max(f[j],f[j - v[i]] + w[i]);
  printf("%lld",f[m]);
  return 0;
}

多重背包

对每一个物品，最多能用 \(t[i]\) 次。

最暴力的方法就是转移的时候枚举这个物品选几个即可。

\[f[i][j] = \max\{f[i - 1][j - v[i] \times k] + w[i] \times k \ \ | \ \ k \leq t[i]\} \]

复杂度 \(O(n \times m \times \sum t[i])\)

\(w\) 和 \(v\) 依旧反着。

优化

二进制拆分

可以把 \(t[i]\) 拆成 \(1,2,4,8 \dots t[i]-2^k\) , 这样 \(k+1\) 组，然后我们会发现这些组能拼成 \(0 \dots t[i]\) 每一种情况，然后这样我们就成了 \(n \times \log(t[i])\)个物品的 0/1 背包问题。

\(1, 2, 4, 8, 16, 32 ,\cdots 2 ^ {63}\)
\(1_{(2)},10_{(2)},100_{(2)},1000_{(2)},10000_{(2)},100000_{(2)}\)
复杂度 \(O(n \times \sum\log(t[i]) \times m)\)

例题 ： 【宝物筛选】

【\(Description\)】

有 \(n\) 种物品，有总容量为 \(m\) 的一个背包，第 \(i\) 个物品的重量为 \(w_i\)，价值为 \(v_i\)，这种物品一共有 \(t_i\) 件。

对于 \(30\%\) 的数据，\(n \leq \sum m_i \leq 10 ^ 4\)，\(0 \leq w \leq 10 ^ 3\)。
对于 \(100\%\) 的数据，\(n \leq \sum m_i \leq 10 ^ 5\)，\(0 \leq w \leq 4 \times 10 ^ 4\)，\(1 \leq n \leq 100\)。

【\(Solution\)】

本来就是一个多重背包的模板题，但是数据范围太大了，用 \(O(n \times m \times \sum t[i])\) 的解法会 T 成 \(30 pts\)。

开始二进制优化，先把原来的数据分为 \(1 - 64\) 块，(这里记着一定要把数组开大点！！！，因为拆分后的数据量最多会乘 64 倍)。

【\(Code\)】

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int Maxk = 1000010;
int n,m,cnt;
int w[Maxk];
int f[Maxk];
int v[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  n = read(),m = read();
  for(int i = 1;i <= n;i ++) {
    int x = read(),y = read(),z = read();
    for(int j = 1;j <= z;j <<= 1) {
      v[++ cnt] = x * j;
      w[cnt] = y * j;
      z -= j;
    }
    if(z) v[++ cnt] = x * z,w[cnt] = y * z;
  }
  for(int i = 1;i <= cnt;i ++) {
    for(int j = m;j >= w[i];j --) {
      f[j] = max(f[j],f[j - w[i]] + v[i]);
    }
  }
  printf("%d",f[m]);
  return 0;
}

单调队列优化

借用一下 \(Nativ\) 的图片 \(\to\)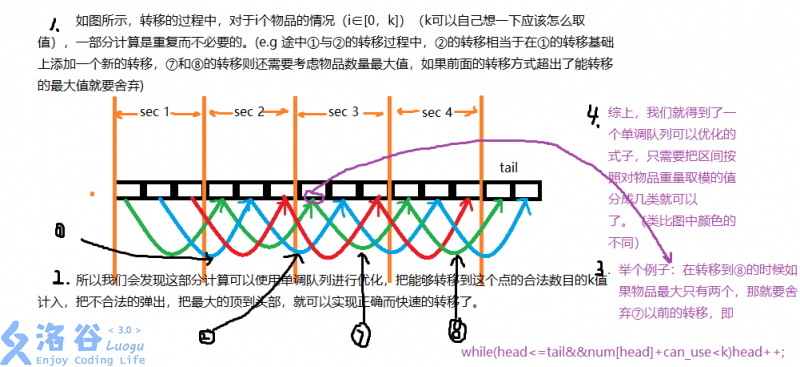

我们来观察一下式子 ：

\[f[i][j] = \max\{f[i - 1][j],f[i - 1][j - k \times v[i]] + k \times w[i] \ \ | \ \ 1 \leq k \leq t[i]\} \]

我们发现对于第二维，我们的 \(j\) 和能转移过来的 \(j - v[i] \times k\) 在模 \(v[i]\) 意义下是同余的，也就是说我们可以对于第二维按照模 \(v[i]\) 的同余类进行分类，不同类之间不会互相影响。

设 \(dp[j] = f[i - 1][j \times v[i] + r]\)，\(r\) 是我们枚举模 \(v[i]\) 的一个类。

\[f[i][j \times v[i] + r] = \max(dp[k] + (j - k) \times w[i] \ \ | \ \ j - k \leq t[i]) \]

\[f[i][j \times v[i] + r] = \max(dp[k] - k \times w[i]\ \ | \ \ j - k \leq t[i]) + j \times w[i] \]

可以用单调队列来解决，用单调队列优化。

\(f[i][j \times v[i] + r] = \max\{f[i - 1][j \times v[i] + r - (j - k) \times v[i]] + (j - k) \times w[i] \ \ | \ \ j - k \leq t[i]\}\)

时间复杂度为 \(O(n \times m)\)。

其实我还是有些不懂。

分组背包

一共有 \(n\) 组，每组有 \(size[i]\) 个物品，第 \(i\) 组第 \(j\) 个物品的费用为 \(w[i][j]\)，价值 \(v[i][j]\)，每个组里的物品是互斥的，意味着你在一组物品中只能选择一个物品，求花费小于等于 \(m\) 能得到的最大价值。

\(\sum size \leq 1000，m \leq 1000\)

都是一样的，只要在输入时建立一个 \(size\) 数组，储存每个数所在的组号，在套上个多重背包枚举即可。

\[f[i][j] = \max _{k = 1} ^ {size_i}(f[i - 1][j - v[i][k]] + w[i][k]) \]

混合背包

就是 0/1 背包，多重背包，完全背包掺杂起来的一种背包类型。

【樱花】

【\(Description\)】

一个人有 \(m\) 的时间欣赏樱花，樱花有 \(n\) 种，樱花有的可以观赏无数次，有的只能观赏有限次，每观察一次第 \(i\) 种樱花会消耗 \(v_i\) 的时间，并得到 \(w_i\) 的美学值，且第 \(i\) 种樱花的可观赏次数为 \(t_i\)(若 \(t\) 为 0 则可以观赏无限次)，求在限定时间里美学值最大是多少。

\(m \leq 10 ^ 3,n \leq 10 ^ 4\)

【\(Solution\)】

显然是一个混合背包，我们可以记录 \(t\)，如果 \(t_i = 0\) 则就套上完全背包，否则套上多重背包。

但是这样只能得到 \(80 pts\)，考虑优化，上面说的二进制优化就可以。

【\(Code\)】

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int Maxk = 1501000;
char a[15],b[15];
int n,m,x,y,cnt;
int op[Maxk],v[Maxk],w[Maxk];
int f[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  scanf("%s %s %d",a + 1,b + 1,&n);
  for(int i = 1;i <= n;i ++) {
    int u = read(),e = read(),z = read();
    if(z == 0) z = 999999;
    for(int j = 1;j <= z;j <<= 1) v[++ cnt] = u * j,w[cnt] = e * j,z -= j;
    if(z) v[++ cnt] = u * z,w[cnt] = e * z;
  }
  if(a[3] == ':') {
    if(strlen(a + 1) == 5) {
      x = ((a[1] - '0') * 10 + (a[2] - '0')) * 60 + ((a[4] - '0') * 10 + a[5] - '0'); 
    }
    else {
      x = ((a[1] - '0') * 10 + (a[2] - '0')) * 60 + (a[4] - '0'); 
    }
  }
  else {
    if(strlen(a + 1) == 4) {
      x = (a[1] - '0') * 60 + ((a[3] - '0') * 10 + a[4] - '0'); 
    }
    else {
      x = (a[1] - '0') + (a[3] - '0'); 
    }
  }
  if(b[3] == ':') {
    if(strlen(b + 1) == 5) {
      y = ((b[1] - '0') * 10 + (b[2] - '0')) * 60 + ((b[4] - '0') * 10 + b[5] - '0'); 
    }
    else {
      y = ((b[1] - '0') * 10 + (b[2] - '0')) * 60 + (b[4] - '0'); 
    }
  }
  else {
    if(strlen(b + 1) == 4) {
      y = (b[1] - '0') * 60 + ((b[3] - '0') * 10 + b[4] - '0'); 
    }
    else {
      y = (b[1] - '0') + (b[3] - '0'); 
    }
  }
  m = y - x;
  for(int i = 1;i <= cnt;i ++) {
    for(int j = m;j >= v[i];j --) {
      f[j] = max(f[j],f[j - v[i]] + w[i]);
    }
  }
  printf("%d",f[m]);
  return 0;
}

总结

做背包问题最关键的就是找清楚并反问自己？

这题里面什么是容量？什么是物品？什么是物品的费用？什么是物品的价值？

  • 容量，就是这题当中我们怎样表示状态的数组。
  • 费用，就是用来 \(f[i] \to f[i+w[k]]\)，状态转移的跨度
  • 价值，就是你这个 \(dp\) 的数组，所维护的东西。维护的数值！

背包 \(dp\) 一定要理解好这三点。

【朴素的网络游戏】

【\(Description\)】

给你一些房间，告诉你这些房间的容纳人数和价格。

安排一定数量的人住到旅馆里，满足：

  • 不同性别的人如果不是夫妻那么不能住一个房间。
  • 一对夫妻如果住在一起，那么房间不能安排其他的人进去哪怕房间没盛满人。

你来写一个程序帮助佳佳找到安排这些来参加旅行的人住进旅馆所需要的最小花费。

  • \(M\)：参加旅行的男性人数
  • \(f\)：参加旅行的女性人数
  • \(r\)：旅馆的房间数
  • \(c\)：这些男女中有多少对夫妻
  • \(B_i\)：每个房子容纳人数和
  • \(P_i\)：每个房子价格。

注意每一个人不是单身就是和他/她唯一的妻子/丈夫一起参加旅行

\(0 \leq m,f,r \leq 300,0 \leq c \leq \min(m,f),0 \leq P_i \leq 10,2 \leq B_i \leq 300\)。

【\(Solution\)】

还是要先明确，对于一道背包 dp 的题目来说，我们需要有 容量，物品，费用，价值（权值，因为有些题要求最小）。

本题中：求给所有的人安排房间的最小支出是多少？那么在这里，几个人对应就是 dp 的数组下标，每个房间就是一个物品，房间支出就是物品的权值。

虽然这里看上去房间支出是花费，是作为数组下标的存在，实际上是作为我们要求的东西，是 dp 数组存的内容，当然肯定不是这么简单就完了的。

首先要观察出题目的一个小性质，即如果有两对(或以上)夫妻住在一起的话，那么交换之后结果不会变差。

因为首先这两个房间的容量至少为 2，如果男男在一个房间，女女在一个房间此时花费不变，有一个房间容量大于 2 的时候，就还可以再入住其他人。这样结果变得更优了。

综上，要么至多存在 1 对夫妻住在一起，要么不存在夫妻住在一起。

\(f[i][j][k][0]\) 表示前 \(i\) 个房间住 \(j\) 名男性 \(k\) 名女性并且没有夫妇住在一起的最小花费。

\(f[i][j][k][0]\) 表示前 \(i\) 个房间住 \(j\) 名男性 \(k\) 名女性并且有一对夫妇住在一起的最小花费。

\[f[i][j][k][0] = \min\{f[i-1][j][k][0],f[i-1][j-v[i]][k][0]+p[i],f[i-1][j][k-v[i]][0]+p[i]\} \]

\[f[i][j][k][1] = \min\{f[i-1][j][k][1],f[i-1][j-v[i]][k][1]+p[i],f[i-1][j][k-v[i]][1]+p[i],f[i - 1][j - 1][k - 1][0] + p[i]\} \]

看的我眼都花了/jk

一类套路题

【梦幻岛宝珠】

【\(Description\)】

给你 \(N\) 颗宝石，每颗宝石都有重量 \(W_i\) 和价值 \(V_i\) 。要你从这些宝石中选取一些宝石，保证总重量不超过 \(W\)，且总价值最大，并输出最大的总价值，每颗宝石的重量符合 \(a \times 2^b\)。

\(V \leq 10^ 9,a \leq 10, b \leq 30\)。

【\(Solution\)】

看到w很大，看似不可做，但是这题肯定能做啊！我们就找有什么特殊的约束条件。

\(w=a \times 2^b\)，我们发现 \(a\)，\(b\) 都不大，就启发我们用 \(2^b\) 分组。

将物品按 \(b\) 值从大到小排序分阶段处理，在阶段内 \(b\) 值都相同，直接忽略不足 \(2^b\) 的部分，\(f[i][j]\) 表示前 \(i\) 个物品，剩余的能用重量为 \(j \times 2^b\) 的最大价值。

\(f[i][j] \gets f[i-1][j+a] + v[i]\)
\(f[i][j] \gets f[i-1][j]\)

从上一阶段到下一阶段时，将 \(f[i][j] \to f[i][j*2+零碎部分]\)，注意到 \(n=100\)，\(a \leq 10\)，所以剩余重量最多纪录到 \(1000\) 即可。

复杂度 \(O（n*1000)\)

二维费用背包

【例题】

【\(Description\)】

给出 \(n\) 个化学反应，每个反应消耗 \(a_i\) 升氧气和 \(b_i\) 升氢气，可以得到 \(w_i\) 的价值，现在总共有 \(X\) 升氧气和 \(Y\) 升氢气，求我们最多可以得到多少价值。

\(n,a_i,b_i,X,Y \leq 100\)。

【\(Solution\)】

二维费用背包问题。

因为限制条件多了一个，所以我们需要给最初最基本的dp多加一维状态。

设 \(dp[i][x][y]\) 表示前 \(i\) 个物品，消耗了 \(x\) 的氧气和 \(y\) 的氢气所能得到的最大收益是多少，然后考虑一个物品选还是不选即可。

【NASA 的计划】

【\(Description\)】

每个物品有 \(v_i\) 的体积和 \(w_i\) 的重量，还有 \(k_i\) 的价值，每个物品你只能用一次，要求在一个体积为 \(V\) ，能承载重量为 \(W\) 的背包中使获得的总价值最高。

【\(Solution\)】

很显然的二维费用背包，套上模板。

\[f[i][j][p] = \max\{f[i - 1][j][p],f[i - 1][j - v[i]][p - w[i]] + k[i]\} \]

在优化一下可以变成两维，看代码。

【\(Code\)】

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int Maxk = 410;
int V,M,n;
int f[Maxk][510];
int v[Maxk],w[Maxk],k[Maxk];
inline int read()
{
	int s = 0, f = 0;char ch = getchar();
	while (!isdigit(ch)) f |= ch == '-', ch = getchar();
	while (isdigit(ch)) s = s * 10 + (ch ^ 48), ch = getchar();
	return f ? -s : s;
}
signed main()
{
  V = read(),M = read();
  n = read();
  for(int i = 1;i <= n;i ++) {
    v[i] = read();
    w[i] = read();
    k[i] = read();
  }
  for(int i = 1;i <= n;i ++) {
    for(int j = V;j >= v[i];j --) {
      for(int h = M;h >= w[i];h --) {
        f[j][h] = max(f[j][h],f[j - v[i]][h - w[i]] + k[i]);
      }
    }
  }
  printf("%d",f[V][M]);
  return 0;
}

总结

说实话自己背包整理的不太好，好多都是只背过了模板。

还未整理 ：

  • 有依赖性的背包
  • 泛化物品
posted @ 2021-03-13 21:19  Ti_Despairy  阅读(92)  评论(0)    收藏  举报