10.Java SDK源码分析系列笔记-TreeMap

目录

• 1. 是什么
• 2. 使用
• 3. 源码分析
  • 3.1. uml
  • 3.2. 构造方法
  • 3.3. put
  • 3.4. get
  • 3.5. containsKey
  • 3.6. remove
• 4. 参考

1. 是什么

基于红黑树（平衡二叉搜索树）实现，效率为O（logN）的key-value对。
迭代时输出的顺序是

• 按照key的自然顺序来遍历的
• 也可以使用自定义的Comparator进行排序

2. 使用

public class TreeMapTest
{
    public static void main(String[] args)
    {
        TreeMap<String, String> map = new TreeMap<>();
        map.put("1", "a");
        map.put("3", "c");
        map.put("2", "b");
        map.put("4", "d");

        for (Map.Entry<String, String> entry : map.entrySet())
        {
            /*
            *   1=a
                2=b
                3=c
                4=d
            * */
            System.out.println(entry);
        }
    }
}

3. 源码分析

3.1. uml

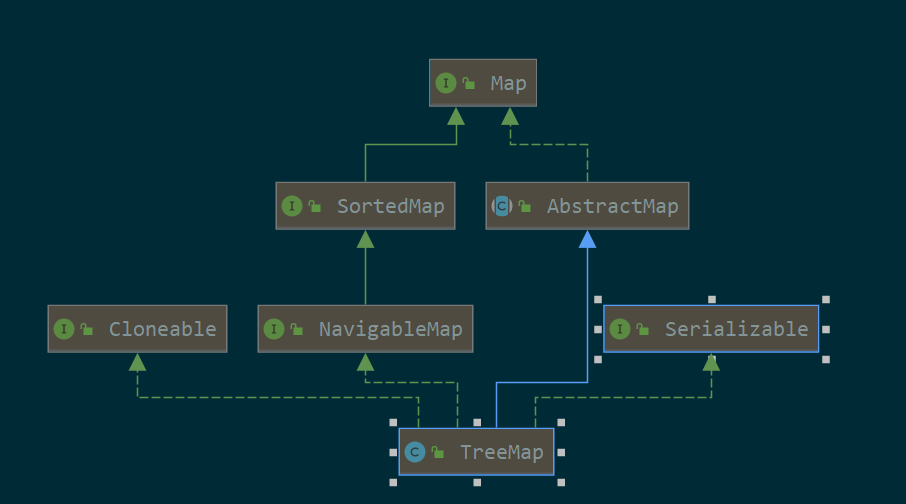
3.2. 构造方法

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable//NavigableMap是个有序的map接口
{

    //使用compartor来排序key
    private final Comparator<? super K> comparator;

	//红黑树的root
    private transient Entry<K,V> root;

    //红黑树的size
    private transient int size = 0;

    private transient int modCount = 0;
    
	//无参构造，默认按key的自然顺序排序
	public TreeMap() {
		comparator = null;
	}

	//自定义comparator进行排序
	public TreeMap(Comparator<? super K> comparator) {
		this.comparator = comparator;
	}
}

3.3. put

public V put(K key, V value) {
	//root节点为空，那么先构造红黑树
    Entry<K,V> t = root;
    if (t == null) {
    	//有自定义的comparator则使用自定义的comparator，否则使用key的compareTo（因此key必须实现Comparable接口）
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    Comparator<? super K> cpr = comparator;
    //有自定义的comparator
    if (cpr != null) {
    	//二叉搜索树的搜索操作
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
        	//比当前节点小走左边
            if (cmp < 0)
                t = t.left;
            //比当前节点大走右边
            else if (cmp > 0)
                t = t.right;
            //找到了，替换value
            else
                return t.setValue(value);
        } while (t != null);
    }
    //没有自定义的comparator
    else {
    	//key必须不为空
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        //逻辑同上
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    //把节点实际插入到树中
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    //维持红黑树的平衡
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

3.4. get

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}


final Entry<K,V> getEntry(Object key) {
    //自定义compartor走这段，实际跟下面的差不多
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    //二叉搜索树的搜索操作，从root节点出发寻找
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

3.5. containsKey

public boolean containsKey(Object key) {
	//简单的调用getEntry方法，同get
    return getEntry(key) != null;
}

3.6. remove

public V remove(Object key) {
	//查到节点
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
	//删除该节点
    deleteEntry(p);
    return oldValue;
}


private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size;


    //删除节点有左右孩子，找到successor节点，并让p指向此节点
    if (p.left != null && p.right != null) {
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    } 

    // 代替删除节点的节点（有左孩子则使用左孩子，否则右孩子）
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

	//使用左孩子或者右孩子替换当前删除节点
    if (replacement != null) {
        // Link replacement to parent
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;

        // 清空删除节点的指针
        p.left = p.right = p.parent = null;

        // 红黑树平衡
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    //树中只有一个节点（就是删除节点）
    } else if (p.parent == null) {
        root = null;
    } else {//没有左右孩子
        if (p.color == BLACK)
        	// 红黑树平衡
            fixAfterDeletion(p);

		//那么修改父节点的指针即可
        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

4. 参考

TreeMap就这么简单【源码剖析】 - 掘金