闵可夫斯基和

闵可夫斯基和主要有两种形式：给定两个凸包 \(A,B\) ，求由向量 \((u+v)_{u \in A, v \in B}\) 构成的凸包；给定平面上任意多个向量，取一个子集求和，求和的模长最值。不难发现两种形式本质上是等价的。

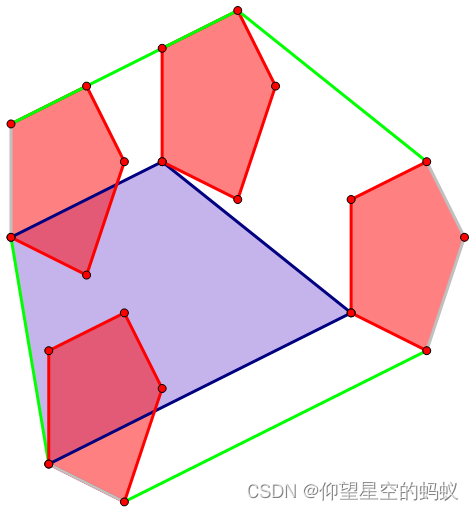
可以发现两个凸包的闵可夫斯基和等价于两个凸包所有边按照斜率排序后顺次首尾相连形成的图形，但直接按照斜率排序可能会出现问题，例如四边形 ABCD 本来应该是 \(AB,BC,CD,DA\)，直接按斜率排序后可能会变成 \(AB,CD,BC,DA\)。所以先对向量按照象限分类，同一象限再按照斜率排序，不同象限象限小者优先。

如果我们需要求最值，此时应该从四个角上开始遍历，也就是 \(x,y\) 分别取最大，最小值的情况，此时需要视排序方式进行一些处理。例如在上面的排序方式中，如果让 \(x\) 坐标取到最小值，会造成横坐标先增加，再缩减，再增加，再缩减，有可能引发同一个向量加两次的情况，如果让 \(y\) 坐标取到最小值就不会出现这样的问题。

code

#include<bits/stdc++.h>
#define int __int128
#define N 200005
#define pb push_back
#define fi first
#define se second
#define pii pair<int,int>
#define MP make_pair
using namespace std;
int n; vector<pii >vi;
namespace io {
	const int __SIZE = (1 << 21) + 1;
	char ibuf[__SIZE], *iS, *iT, obuf[__SIZE], *oS = obuf, *oT = oS + __SIZE - 1, __c, qu[55]; int __f, qr, _eof;
	#define Gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, __SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
	inline void flush () { fwrite (obuf, 1, oS - obuf, stdout), oS = obuf; }
	inline void gc (char &x) { x = Gc(); }
	inline void pc (char x) { *oS ++ = x; if (oS == oT) flush (); }
	inline void pstr (const char *s) { int __len = strlen(s); for (__f = 0; __f < __len; ++__f) pc (s[__f]); }
	inline void gstr (char *s) { for(__c = Gc(); __c < 32 || __c > 126 || __c == ' ';)  __c = Gc();
		for(; __c > 31 && __c < 127 && __c != ' ' && __c != '\n' && __c != '\r'; ++s, __c = Gc()) *s = __c; *s = 0; }
	template <class I> inline bool gi (I &x) { _eof = 0;
		for (__f = 1, __c = Gc(); (__c < '0' || __c > '9') && !_eof; __c = Gc()) { if (__c == '-') __f = -1; _eof |= __c == EOF; }
		for (x = 0; __c <= '9' && __c >= '0' && !_eof; __c = Gc()) x = x * 10 + (__c & 15), _eof |= __c == EOF; x *= __f; return !_eof; }
	template <class I> inline void print (I x) { if (!x) pc ('0'); if (x < 0) pc ('-'), x = -x;
		while (x) qu[++ qr] = x % 10 + '0',  x /= 10; while (qr) pc (qu[qr --]); }
	struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
} using io::pc; using io::gc; using io::pstr; using io::gstr; using io::gi; using io::print;
int calc(pii t){
	if(t.fi>=0&&t.se>0) return 0;
	if(t.fi<=0&&t.se>0) return 1;
	if(t.fi<0&&t.se<=0) return 2; 
	return 3;
}bool cmp(pii x,pii y){
	if(calc(x)!=calc(y)) return calc(x)<calc(y);
	return x.se*y.fi<x.fi*y.se;
}signed main(){
	gi(n); int ans=0,sx=0,sy=0;
	for(int i=1,ai,bi,ci,di;i<=n;i++){
		gi(ai),gi(bi),gi(ci),gi(di);
		vi.pb(MP(ai-bi,ci-di)),vi.pb(MP(bi-ai,di-ci));
		if(ci<di||(ci==di&&ai<bi)) sx+=ai-bi,sy+=ci-di;
	}sort(vi.begin(),vi.end(),cmp),ans=sx*sx+sy*sy;
	print(sx),pc(' '),print(sy),pc('\n');
	for(int i=0;i<(int)vi.size();i++){
		sx+=vi[i].fi,sy+=vi[i].se; ans=max(ans,sx*sx+sy*sy);	
	}print(ans); return 0;
}