机器学习—回归2-3（多项式回归）

使用多项式回归根据年龄预测医疗费用

主要步骤流程：

  • 1. 导入包
  • 2. 导入数据集
  • 3. 数据预处理
    • 3.1 检测缺失值
    • 3.2 筛选数据
    • 3.3 得到因变量
    • 3.4 创建自变量
    • 3.5 检验新的自变量和charges的相关性
    • 3.6 拆分训练集和测试集
  • 4. 构建多项式回归模型
    • 4.1 构建模型
    • 4.2 得到线性表达式
    • 4.3 预测测试集
    • 4.4 得到模型的MSE
  • 5. 构建简单线性回归模型（用于对比）
    • 5.1 构建简单线性回归模型（用于对比）
    • 5.2 预测测试集
    • 5.3 得到模型的MSE
  • 6. 对比2种模型可视化效果

 

  数据集链接：https://www.cnblogs.com/ojbtospark/p/16005626.html
 

1. 导入包

In [2]: 
# 导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

 

2. 导入数据集

In [3]:
# 导入数据集
data = pd.read_csv('insurance.csv')
data.head()
Out[3]:
 agesexbmichildrensmokerregioncharges
0 19 female 27.900 0 yes southwest 16884.92400
1 18 male 33.770 1 no southeast 1725.55230
2 28 male 33.000 3 no southeast 4449.46200
3 33 male 22.705 0 no northwest 21984.47061
4 32 male 28.880 0 no northwest 3866.85520
 

3. 数据预处理

3.1 检测缺失值

In [4]:
# 检测缺失值
null_df = data.isnull().sum()
null_df
Out[4]:
age         0
sex         0
bmi         0
children    0
smoker      0
region      0
charges     0
dtype: int64

3.2 筛选数据

In [5]:
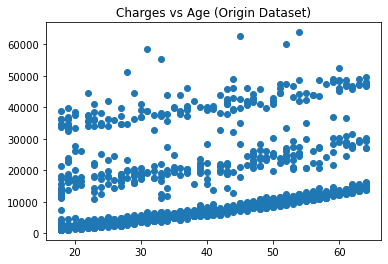
# 画出age和charges的散点图
plt.figure()
plt.scatter(data['age'], data['charges'])
plt.title('Charges vs Age (Origin Dataset)')
plt.show()
In [6]:
# 筛选数据
new_data_1 = data.query('age<=40 & charges<=10000') # 40岁以下 且 10000元以下
new_data_2 = data.query('age>40 & age<=50 & charges<=12500') # 40岁至50岁之间 且 12500元以下
new_data_3 = data.query('age>50 & charges<=17000') # 50岁以上 且 17000元以下
new_data = pd.concat([new_data_1, new_data_2, new_data_3], axis=0)
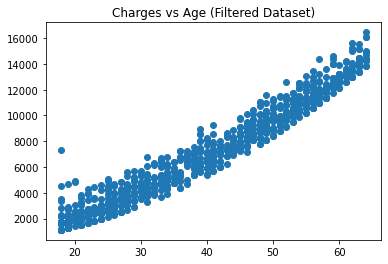
In [7]:
# 画出age和charges的散点图
plt.figure()
plt.scatter(new_data['age'], new_data['charges'])
plt.title('Charges vs Age (Filtered Dataset)')
plt.show()
In [8]:
# 检查age和charges的相关性
print('age和charges的相关性是：\n', np.corrcoef(new_data['age'], new_data['charges']))
age和charges的相关性是：
 [[1.         0.97552029]
 [0.97552029 1.        ]]

3.3 得到因变量

In [9]:
# 得到因变量
y = new_data['charges'].values

3.4 创建自变量

In [10]:
# 创建自变量
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree = 4, include_bias=False)
x_poly = poly_reg.fit_transform(new_data.iloc[:, 0:1].values)
x_poly
Out[10]:
array([[1.8000000e+01, 3.2400000e+02, 5.8320000e+03, 1.0497600e+05],
       [2.8000000e+01, 7.8400000e+02, 2.1952000e+04, 6.1465600e+05],
       [3.2000000e+01, 1.0240000e+03, 3.2768000e+04, 1.0485760e+06],
       ...,
       [5.2000000e+01, 2.7040000e+03, 1.4060800e+05, 7.3116160e+06],
       [5.7000000e+01, 3.2490000e+03, 1.8519300e+05, 1.0556001e+07],
       [5.2000000e+01, 2.7040000e+03, 1.4060800e+05, 7.3116160e+06]])
In [11]:
# 打印age数据
new_data.iloc[:, 0:1]
Out[11]:
 age
1 18
2 28
4 32
5 31
7 37
... ...
1325 61
1327 51
1329 52
1330 57
1332 52

966 rows × 1 columns

3.5 检验新的自变量和charges的相关性

In [12]:
# 检验新的自变量和charges的相关性
corr_df = pd.DataFrame(x_poly, columns=['one','two','three','four'])
corr_df['charges'] = y
print('age的n次幂和charges的相关性是：\n', corr_df.corr(method='pearson'))
age的n次幂和charges的相关性是：
               one       two     three      four   charges
one      1.000000  0.988503  0.960359  0.924344  0.975520
two      0.988503  1.000000  0.991262  0.970392  0.977944
three    0.960359  0.991262  1.000000  0.993638  0.961974
four     0.924344  0.970392  0.993638  1.000000  0.935838
charges  0.975520  0.977944  0.961974  0.935838  1.000000

3.6 拆分训练集和测试集

In [13]:
# 拆分训练集和测试集
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x_poly, y, test_size = 0.2, random_state = 1)

 

4. 构建多项式回归模型

4.1 构建模型

In [14]:
# 构建多项式回归模型
from sklearn.linear_model import LinearRegression
regressor_pr = LinearRegression(normalize = True, fit_intercept = True)
regressor_pr.fit(x_train, y_train)
Out[14]:
LinearRegression(normalize=True)

4.2 得到线性表达式

In [15]:
# 得到线性表达式
print('Charges = %.2f * Age + %.2f * Age^2 + %.2f * Age^3 + %.2f * Age^4 + %.2f' 
      %(regressor_pr.coef_[0], regressor_pr.coef_[1], regressor_pr.coef_[2], regressor_pr.coef_[3], regressor_pr.intercept_))
# Charges = -300.10 * Age + 19.35 * Age^2 + -0.31 * Age^3 + 0.00 * Age^4 + 2687.10
Charges = -300.10 * Age + 19.35 * Age^2 + -0.31 * Age^3 + 0.00 * Age^4 + 2687.10

4.3 预测测试集

In [16]:
# 预测测试集
y_pred_pr = regressor_pr.predict(x_test)

4.4 得到模型的MSE

In [17]:
# 得到模型的MSE
from sklearn.metrics import mean_squared_error
mse_score = mean_squared_error(y_test, y_pred_pr)
print('多项式回归模型的MSE是：%.2f' %(mse_score)) # 654,495.38
多项式回归模型的MSE是：654495.38
 

5. 构建简单线性回归模型（用于对比）

5.1 构建简单线性回归模型（用于对比）

In [18]:
# 构建简单线性回归模型（用于对比）
regressor_slr = LinearRegression(normalize = True, fit_intercept = True)
regressor_slr.fit(x_train[:,0:1], y_train)
Out[18]:
LinearRegression(normalize=True)

5.2 预测测试集

In [19]:
# 预测测试集
y_pred_slr = regressor_slr.predict(x_test[:,0:1])

5.3 得到模型的MSE

In [20]:
# 得到模型的MSE
mse_score = mean_squared_error(y_test, y_pred_slr)
print('简单线性回归模型的MSE是：%.2f' %(mse_score))
简单线性回归模型的MSE是：738002.02
 

6. 对比2种模型可视化效果

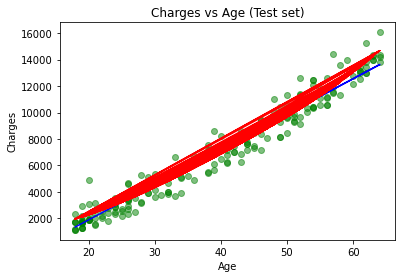
In [21]:
# 可视化测试集预测结果
plt.scatter(x_test[:,0], y_test, color = 'green', alpha=0.5)
plt.plot(x_test[:,0], y_pred_slr, color = 'blue')
plt.plot(x_test[:,0], y_pred_pr, color = 'red')
plt.title('Charges vs Age (Test set)')
plt.xlabel('Age')
plt.ylabel('Charges')
plt.show()
 

结论： 1）上图绿色点是样本点，红色点是多项式回归的拟合结果，蓝色点是简单线性回归的拟合结果。2种模型拟合效果都较好；

　　　 2）根据MSE，多项式回归模型性能略胜一筹；

 

 

 

posted @ 2022-03-15 16:40  Theext  阅读(318)  评论(0)    收藏  举报