洛谷P5325 【模板】Min_25筛

https://www.luogu.com.cn/problem/P5325

 

%%%%大佬的题解%%%%%

https://www.luogu.com.cn/blog/wucstdio/solution-p5325

https://www.cnblogs.com/zhoushuyu/p/9187319.html

https://www.cnblogs.com/cjyyb/p/9185093.html

 

个人理解&&要点记录：

1、使用条件：

①F(x)是积性函数

②F(p)是关于p的简单多项式，F(p^c)可快速求，p是质数

2、结果的计算方式：多项式拆出的若干个单项式分别计算的和

 

对于每个单项式 f(i)=i^k

minp表示i的最小质因子

pj表示第j个质数

预处理g(n,j)=Σf(i)   i是质数或者minp>pj，i∈[1,n]

采用类似于dp的方式  （其中除法需要向下取整）

意思是

1到n内，i是质数或者最小质因子大于第j个质数的f(i)之和

等于

1到n内 i是质数或者最小质因子大于第j-1个 质数的 f(i)之和 ，减去1到n内 i的最小质因子是第j个质数的f(i)之和

将满足最小质因子是第j个质数的i 提取一个pj出来

因为这里对每个单项式分开计算，所以可以直接提取pj为f(pj）

提取出来后，只要剩余的质因子不小于第j个质数即可，所以是g(n/pj,j-1)

g(n/pj，j-1)中还包含了多减的前j-1个质数，所以要减去

 

g的第二维可以用压维的方式压去

但是我们不能对1-n内的每个数都算一次g(i)

(以下除法都表示下取整）

在求g(n)的时候，用到的是g(n/pa)

求g(n/pa)，用到的是g(n/pa/pb)

n/pa/pb=n/(pa*pb)  （除法下取整）

所以一共用到的就是使 n/i=x，x不同的个数

它的个数是根号级别的

证明：

当i<=根号n时，n/i=x （下取整） ,不同的x不超过根号n个

当i>根号n时，n/(n/i)=x （下取整），因为n/i<根号n，所以不同的 x也不超过根号n个

那么我们将这 根号n级别的数离散化一下

若x<=根号n，令id1[x]=编号

若x>根号n，令id2[n/x]=编号

这样就可以将空间复杂度控制在根号n

 

预处理完成后，开始求题目要求的函数

此时对每个单项式都得到了一个数组g[n]，表示[1,n]内的质数对于该单项式的贡献

用这些单项式的和即可得到最终的答案

令S(n,j)=ΣF(i) i∈[1,n]且minp>Pj

S的计算分为质数和合数2个部分

质数就是 g[n]-ΣF(Pi), i<=j

对于合数

因为F是积性函数，所以

枚举最小质因子Pk，Pk*Pk<=n

枚举Pk的指数e，Pk^(e+1)<=n

即这个合数分解质因子有一项是Pk^e，且其他的项是比第k个质数更大的质因子

他满足了积性函数 若gcd(a,b)=1,则F(a)*F(b)=F(ab)

这样还漏了只有Pk这一种质因子的合数

所以还需要另外加上 Pk^2  Pk^3   …… Pk^(e+1)

所以S的式子如下

 

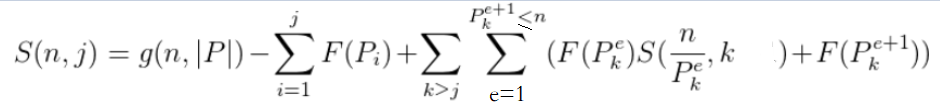
 最终输出S(n,0)+F(1)

 

#include<cstdio>
#include<cmath>
 
using namespace std;

#define N 1000001
const int mod=1e9+7;
typedef long long LL;

LL n;
int sq,id1[N],id2[N];
int m;
LL w[N];
LL g1[N],g2[N];

int tot,pri[N];
bool vis[N];

LL spri[N],spri2[N];

LL inv6;

LL poww(LL a,LL b)
{
    LL s=1;
    for(;b;b>>=1,a=a*a%mod)
        if(b&1) s=s*a%mod;
    return s;
}

void pre()
{
    for(int i=2;i<=sq;++i)
    {
        if(!vis[i]) 
        {
            pri[++tot]=i;
            spri2[tot]=(spri2[tot-1]+1ll*i*i%mod)%mod;
            spri[tot]=(spri[tot-1]+i)%mod;
        }
        for(int j=1;j<=tot && 1ll*i*pri[j]<=sq;++j)
        {
            vis[i*pri[j]]=true;
            if(!(i%pri[j])) break;
        }
    }
    LL j;
    for(LL i=1;i<=n;i=j+1)
    {
        j=n/(n/i);
        w[++m]=n/i;
        if(w[m]<=sq) id1[w[m]]=m;
        else id2[n/w[m]]=m;
        g2[m]=(w[m]%mod)*((w[m]+1)%mod)%mod*((w[m]*2+1)%mod)%mod*inv6%mod-1;
        g1[m]=(w[m]%mod)*((w[m]+1)%mod)/2%mod-1;
    }
}

void solve1()
{
    int k;
    for(int j=1;j<=tot;++j)
        for(int i=1;i<=m && 1ll*pri[j]*pri[j]<=w[i];++i)
        {
            k= w[i]/pri[j]<=sq ? id1[w[i]/pri[j]] : id2[n/(w[i]/pri[j])];
            g2[i]-=1ll*pri[j]*pri[j]%mod*(g2[k]-spri2[j-1])%mod;
            if(g2[i]<0) g2[i]+=mod;
            g1[i]-=1ll*pri[j]*(g1[k]-spri[j-1])%mod;
            if(g1[i]<0) g1[i]+=mod;
        }
}

LL solve2(LL nn,int j)
{
    if(nn<=pri[j]) return 0;
    int kk= nn<=sq ? id1[nn] : id2[n/nn];
    LL g=(g2[kk]-g1[kk]-(spri2[j]-spri[j]))%mod;
    while(g<0) g+=mod; 
    LL now;
    LL sum=0;
    for(int k=j+1;k<=tot && 1ll*pri[k]*pri[k]<=nn;++k)
    {
        now=pri[k]; 
        for(;now*pri[k]<=nn;now*=pri[k])
        {
            sum+=now%mod*((now-1)%mod)%mod*solve2(nn/now,k)%mod;
            sum+=now%mod*pri[k]%mod*(now%mod*pri[k]%mod-1)%mod;
            sum%=mod;
        }
    }
    return (g+sum)%mod;
}

int main()
{
    scanf("%lld",&n);
    sq=sqrt(n);
    inv6=poww(6,mod-2);
    pre();
    solve1();
    printf("%lld",solve2(n,0)+1);
}

 

 同时给我大凶我深感荣幸。。。