2021 icpc 昆明 J-Parallel Sort（思维）

题意：

给出一个长度为 $n$ 的全排列，每次操作可以选择多个二元组$<x_i,y_i>$ ，然后交换$a[x_i]$与$a[y_i]$ ,二元组中的值不能相等，即每个位置在一次操作中只能选择一次。问最少要多少次操作才能使得全排列为升序。

题解：

先说结论：如果不需要交换或者两两之间一次交换就可以满足，那操作数就是$0/1$ ,其他情况就是$2$ 。

我们可以由数组构建出若干个环，比如 4 3 2 1 ，1有一条有向边连向4 ，2有一条有向边连向3，3有一条有向边连向2 ，4有一条有向边连向1，这些有向边代表$u$位置想要交换到$v$ 。如图：

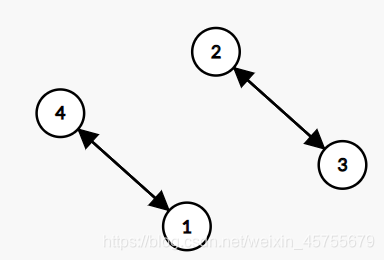
像这样的环，可以通过一次操作完成。

但是 2 5 1 3 4 就不行，如图：

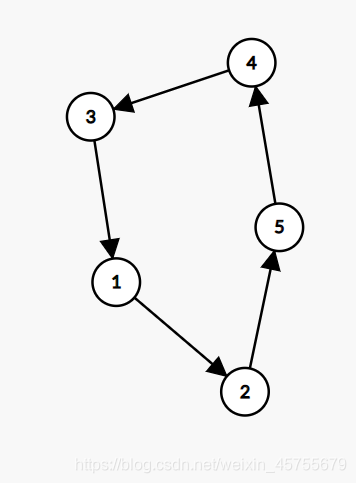
那么怎么实现两次操作完成排序呢？

我们可以把这幅图看作是一个正五边形，进行对称交换，即先交换 $(1,5),(3,4)$ 那么可以发现，2想要5位置的数，5想要4位置的数，3想要1位置的数，这么操作后，2就想要1位置的数，1想要2位置的数，5想要3位置的数，3想要5位置的数，那么不就转变成两两互连的情况了吗。

当环再大一点的时候，同样也满足上述方法，可以画个图试一试。

代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<stack>
#include<set>
#include<ctime>
#define iss ios::sync_with_stdio(false)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<int,int> pii;
const int mod=1e9+7;
const int MAXN=1e5+5;
const int inf=0x3f3f3f3f;
int n;
int a[MAXN];
int id[MAXN];
int nex[MAXN];
int vis[MAXN];
int num[MAXN];
int tot;
std::vector<pii>ans;
void dfs(int u)
{
    if(vis[u]) return;
    vis[u]=1;
    num[++tot]=u;
    dfs(nex[u]);
}
int main()
{
    scanf("%d",&n);
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        id[a[i]]=i;
    }
    int flag=0;
    for(int i=1;i<=n;i++)
    {
        if(a[i]==i)
        {
            nex[i]=0;
        }
        else
        {
            nex[i]=a[i];
            cnt++;
            if(a[i]==id[i])
            {
                if(flag!=2) flag=1;
            }
            else flag=2;
        }
    }
    if(!flag)
    {
        printf("0\n");
        return 0;
    }
    if(flag==1)
    {
        printf("1\n");
        printf("%d ",cnt/2);
        for(int i=1;i<=n;i++)
        {
            if(nex[i])
            {
                printf("%d %d ",i,nex[i]);
                nex[nex[i]]=0;
                nex[i]=0;
            }
        }
        return 0;
    }
    printf("2\n");
    for(int i=1;i<=n;i++)
    {
        if(nex[i]&&!vis[i])
        {
            tot=0;
            dfs(i);
            if(tot&1)
            {
                for(int j=2;j<=2+tot/2-1;j++)
                {
                    ans.push_back(make_pair(num[j],num[tot+2-j]));
                }
            }
            else
            {
                for(int j=1;j<=tot/2;j++)
                {
                    ans.push_back(make_pair(num[j],num[tot+1-j]));
                }
            }
        }
    }
    printf("%d ",ans.size());
    for(int i=0;i<ans.size();i++)
    {
        printf("%d %d ",ans[i].first,ans[i].second);
        swap(a[ans[i].first],a[ans[i].second]);
    }
    printf("\n");
    memset(nex,0,sizeof nex);
    for(int i=1;i<=n;i++)
    {
        id[a[i]]=i;
    }
    cnt=0;
    for(int i=1;i<=n;i++)
    {
        if(a[i]==i)
        {
            nex[i]=0;
        }
        else
        {
            nex[i]=a[i];
            cnt++;
        }
    }
    printf("%d ",cnt/2);
    for(int i=1;i<=n;i++)
    {
        if(nex[i])
        {
            printf("%d %d ",i,nex[i]);
            nex[nex[i]]=0;
            nex[i]=0;x
        }
    }
}