CodeForces - 1359E Modular Stability (思维，数学)

题意：

在$[1,n]$中选k个不同的数从小到大组成数组$a$ ,使得对于任意的数$x$都满足：

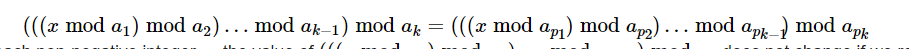
后面为数组$a$的全排列，求有多少种选法。

题解：

先说结论：只需满足$a_1$ 为其他数的因子即可。

证明:

假设$a_2$不是$a_1$的因子 ，那么假设 $x$=$a_2$ ,那么 $x\%a_1\%a_2!=0$ ,但是 $x\%a_2\%a_1==0$ 。

再来看为什么为因子就行。假设 $a_2$和$a_3$ 能整除$a_1$ 那么 $x\%a_2\%a_3\%a_1=(x-x/a_2\ast a_2)\%a_3\%a_1$

$->$ $((x-x/a_2\ast a_2)-(x-x/a_2\ast a_2)/a_3\ast a_3)\%a_1=x\%a_1$

那么最后答案就是 $\sum _{i=1}^{n}C(n/i-1,k-1)$

代码：

#pragma GCC diagnostic error "-std=c++11"
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<stack>
#include<set>
#include<ctime>
#define iss ios::sync_with_stdio(false)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<int,int> pii;
const int mod=998244353;
const int MAXN=5e5+5;
const int inf=0x3f3f3f3f;
ll fac[MAXN];
void cal()
{
    fac[0]=1;
    for(int i=1; i<MAXN; i++)
        fac[i]=fac[i-1]*i%mod;
}
ll qpow(ll a,ll b)
{
    ll ans=1;
    for(; b; b>>=1,a=a*a%mod)
        if(b&1)
            ans=ans*a%mod;
    return ans;
}

ll C(ll n,ll m)
{
    if(n<m)
        return 0;
    return fac[n]*qpow(fac[n-m]*fac[m]%mod,mod-2)%mod;
}
int main()
{
    cal();
    int n,k;
    cin>>n>>k;
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
        int cnt=n/i;
        ans=(ans+C(cnt-1,k-1))%mod;
    }
    printf("%lld\n",ans);
}