暑假集训CSP提高模拟23
暑假集训CSP提高模拟23
组题人: @KafuuChinocpp | @H_Kaguya

\(T1\) P221. 进击的巨人 \(5pts\)
-
部分分
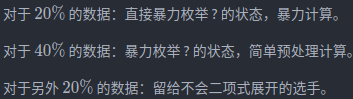
-
正解
-
观察到
0会把区间分成若干个部分,这若干个部分之间互不影响。设 \(cnt_{i}\) 表示 \([1,i]\) 中?的个数。假设我们我们当前枚举的部分为 \([L,R]\) ,其中仅包含1或?。其对答案的贡献为 \(\begin{aligned} &\sum\limits_{l=L}^{R}\sum\limits_{r=l}^{R}(r-l+1)^{k} \frac{1}{2^{cnt_{r}-cnt_{l-1}}} \\ &=\sum\limits_{l=L}^{R}\sum\limits_{r=l}^{R}\sum\limits_{i=0}^{k}\dbinom{k}{i}r^{k-i}(-l+1)^{i} \frac{1}{2^{cnt_{r}-cnt_{l-1}}} \\ &=\sum\limits_{i=0}^{k}\dbinom{k}{i}\sum\limits_{l=L}^{R}\sum\limits_{r=l}^{R}r^{k-i}(-l+1)^{i} \frac{2^{cnt_{l-1}}}{2^{cnt_{r}}} \\ &=\sum\limits_{i=0}^{k}\dbinom{k}{i}\sum\limits_{r=L}^{R} \frac{r^{k-i}}{2^{cnt_{r}}}\sum\limits_{l=L}^{r}(-l+1)^{i} 2^{cnt_{l-1}} \end{aligned}\) 。枚举 \(i\) ,前缀和维护后半部分即可。点击查看代码
const ll p=998244353; char s[100010]; ll cnt[100010]; ll qpow(ll a,ll b,ll p) { ll ans=1; while(b) { if(b&1) { ans=ans*a%p; } b>>=1; a=a*a%p; } return ans; } ll C(ll n,ll m,ll p) { if(n>=m&&n>=0&&m>=0) { ll up=1,down=1; for(ll i=n-m+1;i<=n;i++) { up=up*i%p; } for(ll i=1;i<=m;i++) { down=down*i%p; } return up*qpow(down,p-2,p)%p; } else { return 0; } } ll ask(ll l,ll r,ll k) { ll sum,ans=0; for(ll i=0;i<=k;i++) { sum=0; for(ll j=l;j<=r;j++) { sum=(sum+qpow(-j+1,i,p)*qpow(2,cnt[j-1]-cnt[l-1],p)%p+p)%p; ans=(ans+((C(k,i,p)*qpow(j,k-i,p))%p*qpow(qpow(2,cnt[j]-cnt[l-1],p),p-2,p)%p)*sum%p)%p; } } return ans; } int main() { freopen("attack.in","r",stdin); freopen("attack.out","w",stdout); ll n,k,ans=0,i,l,r; cin>>n>>k>>(s+1); for(i=1;i<=n;i++) { cnt[i]=cnt[i-1]+(s[i]=='?'); } for(l=r=1;l<=n;l++) { if(s[l]!='0') { r=l; while(r<=n&&s[r]!='0') { r++; } r--; ans=(ans+ask(l,r,k))%p; l=r; } } cout<<ans<<endl; fclose(stdin); fclose(stdout); return 0; } -
@hh弟中弟 还有类似 luogu P1654 OSU! 维护幂次对答案贡献的做法,详见 站外题求助 。
-
\(T2\) P226. Wallpaper Collection \(35pts\)
-
感觉状态设计和优化很逆天,将官方题解改了改。
-
部分分
- \(20 \sim 30pts\)
-
设 \(f_{i,l,r}\) 表示第 \(i\) 行选择的区间为 \([l,r]\) 时最大的喜爱值之和,状态转移方程为 \(f_{i,l,r}=\max\limits_{\max(l,L) \le \min(r,R)}\{ f_{i-1,L,R} \}+\sum\limits_{j=l}^{r}a_{i,j}\) 。
-
时间复杂度为 \(O(nm^{4})\) 。
点击查看代码
ll a[1010][1010],sum[1010][1010],f[2][1010][1010]; int main() { freopen("WallpaperCollection.in","r",stdin); freopen("WallpaperCollection.out","w",stdout); ll n,m,ans=-0x7f7f7f7f7f7f7f7f,maxx,i,j,k,l,r; scanf("%lld%lld",&n,&m); for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { scanf("%lld",&a[i][j]); sum[i][j]=sum[i][j-1]+a[i][j]; } } memset(f,-0x3f,sizeof(f)); for(i=1;i<=m;i++) { for(j=i;j<=m;j++) { f[0][i][j]=0; } } for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { for(k=j;k<=m;k++) { maxx=-0x7f7f7f7f7f7f7f7f; for(l=1;l<=j-1;l++) { for(r=j;r<=m;r++) { maxx=max(maxx,f[(i-1)&1][l][r]+sum[i][k]-sum[i][j-1]); } } for(l=j;l<=k;l++) { for(r=l;r<=m;r++) { maxx=max(maxx,f[(i-1)&1][l][r]+sum[i][k]-sum[i][j-1]); } } f[i&1][j][k]=maxx; } } } for(i=1;i<=m;i++) { for(j=i;j<=m;j++) { ans=max(ans,f[n&1][i][j]); } } printf("%lld\n",ans); fclose(stdin); fclose(stdout); return 0; }
-
- \(40pts\)
- \(\max(l,L) \le \min(r,R)\) 等价于 \([L,R]\) 与 \([l,r]\) 有交,即存在一个 \(j \in [l,r]\) 使得 \([L,R]\) 包含 \(j\) 。不妨钦定 \(j\) 然后进行转移。
- 具体地,预处理 \(g_{i,j}=\max\limits_{l \le j \le r} \{ f_{i,l,r} \}\) ,则 \(f_{i,l,r}=\max\limits_{j=l}^{r}\{ g_{i-1,j} \}+\sum\limits_{j=l}^{r}a_{i,j}\) 。
- 时间复杂度为 \(O(nm^{3})\) 。
- \(60pts\)
- 区间有交等价于相邻两行均满足四连通,考虑优化状态设计。
- 设 \(f_{i,j}\) 表示第 \(i\) 行起始位置/钦定选择位置为 \(j\) 时的最大的喜爱值之和。设 \(i-1\) 行起始位置/钦定选择位置为 \(k\) ,则 \(i\) 行所选择的区间 \([L,R]\) 一定满足 \(\begin{cases} L \le \min(j,k) \\ \max(j,k) \le R \end{cases}\) ,此时转移为 \(f_{i,j}=\max\limits_{k=1}^{m} \{f_{i-1,k}+\max\limits_{L \le \min(j,k) \land \max(j,k) \le R}\{ \sum\limits_{h=L}^{R}a_{i,h} \} \}\) 。
- 官方题解上这里是有转化题意铺垫的 ,挂一下转化题面,但感觉还是不如钦定选择一个元素好理解。
- 转化题意
- 想象主人公面前有一个 \(n + 2\) 行 \(m\) 列的矩阵,从第 \(0\) 行一个位置开始,他有如下几种操作:
- 向左移动一个单位,并收集所到达位置上的壁纸。
- 向右移动一个单位,并收集所到达位置上的壁纸。
- 向下移动一个单位,并收集所到达位置上的壁纸。
- 其中第 \(0\) 行和第 \(n + 1\) 行没有壁纸,一个壁纸不能被收集多次,到达第 \(n + 1\) 行时收集结束。
- 最大化收集的壁纸的喜爱值之和。
- 官方题解上这里是有转化题意铺垫的 ,挂一下转化题面,但感觉还是不如钦定选择一个元素好理解。
- 把 \(\max\limits_{L \le \min(j,k) \land \max(j,k) \le R}\{ \sum\limits_{h=L}^{R}a_{i,h} \}\) 拆开后线段树就可以维护最大前/后缀和做了,但先不要着急,式子还能再拆。
- 记 \(s_{i,j}=\sum\limits_{k=1}^{j}a_{i,k},t_{i,j}=\sum\limits_{k=j}^{m}a_{i,k}\) ,那么 \(\sum\limits_{h=L}^{R}a_{i,h}=s_{i,m}-s_{i,L-1}-t_{i,R+1}\) 。负号放到 \(\max\) 里面维护前后缀 \(\min\) 即可。
- 时间复杂度为 \(O(nm^{2})\) 。
- \(20 \sim 30pts\)
-
正解
- 对 \(j,k\) 大小关系进行分讨。
- 假设 \(k \le j\) ,则有 \(f_{i,j}=\max\limits_{k=1}^{j}\{ f_{i-1,k}+s_{i,m}-\min\limits_{h=1}^{k-1}\{ s_{i,h} \}-\min\limits_{h=j+1}^{m}\{ t_{i,h} \} \}\) 。
- 再做一次前后缀 \(\min\) 维护即可。
- 时间复杂度为 \(O(nm)\) 。
点击查看代码
ll a[1010][1010],f[1010][1010],s[1010][1010],t[1010][1010],mins[1010][1010],mint[1010][1010],g[1010],h[1010]; int main() { freopen("WallpaperCollection.in","r",stdin); freopen("WallpaperCollection.out","w",stdout); ll n,m,ans=-0x7f7f7f7f7f7f7f7f,i,j; cin>>n>>m; for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { cin>>a[i][j]; } } for(i=1;i<=n;i++) { g[0]=-0x7f7f7f7f7f7f7f7f; for(j=1;j<=m;j++) { g[j]=max(g[j-1],f[i-1][j]-mins[i][j-1]); s[i][j]=s[i][j-1]+a[i][j]; mins[i][j]=min(mins[i][j-1],s[i][j]); } h[m+1]=-0x7f7f7f7f7f7f7f7f; for(j=m;j>=1;j--) { h[j]=max(h[j+1],f[i-1][j]-mint[i][j+1]); t[i][j]=t[i][j+1]+a[i][j]; mint[i][j]=min(mint[i][j+1],t[i][j]); } for(j=1;j<=m;j++) { f[i][j]=-0x7f7f7f7f7f7f7f7f; } for(j=1;j<=m;j++) { f[i][j]=max(f[i][j],h[j]+s[i][m]-mins[i][j-1]); } for(j=m;j>=1;j--) { f[i][j]=max(f[i][j],g[j]+s[i][m]-mint[i][j+1]); } } for(i=1;i<=m;i++) { ans=max(ans,f[n][i]); } cout<<ans<<endl; fclose(stdin); fclose(stdout); return 0; }
\(T3\) P232. 樱花庄的宠物女孩 \(50pts\)
-
部分分
- 随机 \(pts\) :乱搞。

-
正解
- 人显然需要先走到一个与箱子相邻的节点 \(y\) 然后开始拉着箱子跑。
- 因为边权只有 \(1\) ,故可以 \(BFS\) 处理出 \(x\) 在不经过 \(1\) 的情况下到与 \(1\) 相连的节点的最短路长度 \(dis\) 。
- 容易用 \((u,v,k)\) 来表示箱子在 \(u\) 且人在 \(v\) 时到达该状态的最小步数 \(k\) ,合法状态的数量级为 \(O(m)\) 。初始状态为 \((1,y,dis_{y})\) ,其中 \((1,y) \in E\) 。
- 然后考虑对边(将边的编号加入队列)进行 \(BFS\) 。具体地,取出队首状态 \((u,v,k)\) ,枚举所有与 \(v\) 相连的点进行转移。另外 \(v\) 被访问过两边后就不会再产生更新(说明有环),及时停止来保证复杂度。同时队列中应保证更新过程中 \(k\) 是单调递增的,在加入 \(y\) 的过程中可以双指针或用堆来维护。
- 最后枚举与 \(n\) 相连的边进行判断即可。
点击查看代码
struct node { int nxt,from,to; }e[2000010]; int head[2000010],dis[2000010],vis[2000010],cnt=1; vector<pair<int,int> >pt; void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].from=u; e[cnt].to=v; head[u]=cnt; } void bfs1(int s) { memset(dis,0x3f,sizeof(dis)); queue<int>q; dis[s]=0; q.push(s); while(q.empty()==0) { int x=q.front(); q.pop(); for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to==1) { pt.push_back(make_pair(i^1,dis[x])); } else { if(dis[e[i].to]==0x3f3f3f3f) { dis[e[i].to]=dis[x]+1; q.push(e[i].to); } } } } } void bfs2() { memset(dis,0x3f,sizeof(dis)); memset(vis,0,sizeof(vis)); queue<int>q; for(int i=0;i<pt.size();i++) { dis[pt[i].first]=pt[i].second; } int k=0; while(q.empty()==0||k<pt.size()) { if(q.size()==0) { if(k<pt.size()) { q.push(pt[k].first); k++; } } else { int x=q.front(); q.pop(); if(vis[e[x].to]<=1) { vis[e[x].to]++; while(k<pt.size()&&pt[k].second==dis[x]) { q.push(pt[k].first); k++; } for(int i=head[e[x].to];i!=0;i=e[i].nxt) { if(e[i].to!=e[x].from) { if(dis[i]>dis[x]+1) { dis[i]=dis[x]+1; q.push(i); } } } } } } } int main() { freopen("Sakura.in","r",stdin); freopen("Sakura.out","w",stdout); int n,m,x,u,v,ans=0x7f7f7f7f,i; cin>>n>>m>>x; for(i=1;i<=m;i++) { cin>>u>>v; add(u,v); add(v,u); } bfs1(x); bfs2(); for(i=head[n];i!=0;i=e[i].nxt) { if(dis[i]!=0x3f3f3f3f) { ans=min(ans,dis[i]); } } if(ans==0x7f7f7f7f) { cout<<"No"<<endl; } else { cout<<"Yes"<<endl; cout<<ans<<endl; } fclose(stdin); fclose(stdout); return 0; }
\(T4\) P201. 机动车驾驶员考试 \(0pts\)
-
做法比较抽象,暴力代码都不知道怎么写,挂一下官方题解。
发现无论以时间为轴维护距离,还是以距离为轴维护时间,都会遇到一个问题:取模之后无法比较大小,也就没法在平衡树里操作;线段树的深度会退化到 \(O(n)\) 。
因此需要维护其他东西。
定义“等效距离”,初始的剩余等效距离为 \(x\) ,每秒等效距离减 \(1\) ,那么每次速度减半就等价于剩余等效距离 \(\times 2\) 。
构造一个时间为下标线段树,维护三个值:
\(k\) : 区间减速次数。
\(x\) : 至少需要多少等价距离才可以通过这个时间区间。
\(r\) : 以 \(x\)(即最少需要的等价距离)的等价距离通过这个区间之后,还剩多少等价距离。
注意,此时已经没有速度的概念了。减速已经转化为了等价距离这样的线断树就足以维护添加、合并、查询了。
但是还有一些细节需要讨论:
我们还需要维护 \(r\) 是否已经被取模过了。
由于减速时间点最大为 \(10^9\) ,因此一旦等价距离被取模过 \(\ge 10^9\) ,则一定会通过所有时间节点。
是否取模会有一些简单但繁琐的讨论,可以参考 std 代码。
点击查看 std 代码
#include <cstdio> #include <algorithm> using namespace std; const int max1 = 5e5; const int mod = 1e9 + 7; const int inf = 0x3f3f3f3f; int q; struct Question { int op, x; }qus[max1 + 5]; int save[max1 + 5], len; int power[max1 + 5]; struct Data { int L, R, x, k, r, op; Data operator + ( const Data &A ) const { int dis = save[A.L] - save[R]; Data res; res.L = L; res.R = A.R; res.k = k + A.k; if ( !op && !A.op ) { if ( r - dis - A.x >= 0 ) { res.x = x; if ( A.k <= 30 ) { long long p = (0LL + r - dis - A.x) * (1LL << A.k) + A.r; if ( p >= mod ) { res.op = 1; res.r = p % mod; } else { res.op = 0; res.r = p; } } else if ( !(r - dis - A.x) ) { res.op = 0; res.r = A.r; } else { res.op = 1; res.r = ((0LL + r - dis - A.x) * power[A.k] + A.r) % mod; } } else { int c = ((A.x + dis - r - 1) >> min(31, k)) + 1; res.x = x + c; if ( k <= 30 && A.k <= 30 ) { long long p = (0LL + r - dis - A.x + (c << k)) * (1LL << A.k) + A.r; if ( p >= mod ) { res.op = 1; res.r = p % mod; } else { res.op = 0; res.r = p; } } else if ( k <= 30 && !(r - dis - A.x + (c << k)) ) { res.op = 0; res.r = A.r; } else { res.op = 1; res.r = ((0LL + r - dis - A.x + 1LL * power[k] * c + mod) % mod * power[A.k] + A.r) % mod; } } } else if ( !op && A.op ) { if ( r - dis - A.x >= 0 ) { res.op = 1; res.x = x; res.r = ((0LL + r - dis - A.x) * power[A.k] + A.r) % mod; } else { int c = ((A.x + dis - r - 1) >> min(31, k)) + 1; res.op = 1; res.x = x + c; res.r = ((0LL + r - dis - A.x + 1LL * power[k] * c + mod) % mod * power[A.k] + A.r) % mod; } } else { res.x = x; res.op = 1; res.r = ((0LL + r - dis - A.x + mod) * power[A.k] + A.r) % mod; } return res; } }; struct Segment_Tree { #define lson(now) (now << 1) #define rson(now) (now << 1 | 1) Data tree[max1 * 4 + 5], ans; void Build ( int now, int L, int R ) { if ( L == R ) { tree[now].L = tree[now].R = L; tree[now].x = tree[now].k = tree[now].r = 0; tree[now].op = 0; return; } int mid = (L + R) >> 1; Build(lson(now), L, mid); Build(rson(now), mid + 1, R); tree[now] = tree[lson(now)] + tree[rson(now)]; // printf("Build L = %d R = %d x = %d k = %d r = %d op = %d\n", L, R, tree[now].x, tree[now].k, tree[now].r, tree[now].op); return; } void Insert ( int now, int L, int R, int pos ) { if ( L == R ) { ++tree[now].k; return; } int mid = (L + R) >> 1; if ( pos <= mid ) Insert(lson(now), L, mid, pos); else Insert(rson(now), mid + 1, R, pos); tree[now] = tree[lson(now)] + tree[rson(now)]; return; } void Query ( int now, int L, int R, int x ) { if ( L == R ) return; int mid = (L + R) >> 1; Data res = ans + tree[lson(now)]; if ( res.x > x ) Query(lson(now), L, mid, x); else ans = res, Query(rson(now), mid + 1, R, x); return; } }Tree; int main () { scanf("%d", &q); for ( int i = 1; i <= q; i ++ ) { scanf("%d%d", &qus[i].op, &qus[i].x); if ( qus[i].op == 1 ) save[++len] = qus[i].x; } save[++len] = 0, save[++len] = inf; sort(save + 1, save + 1 + len); len = unique(save + 1, save + 1 + len) - (save + 1); power[0] = 1; for ( int i = 1; i <= q; i ++ ) power[i] = (power[i - 1] << 1) % mod; Tree.Build(1, 1, len); for ( int i = 1; i <= q; i ++ ) { if ( qus[i].op == 1 ) { qus[i].x = lower_bound(save + 1, save + 1 + len, qus[i].x) - save; Tree.Insert(1, 1, len, qus[i].x); } else { Tree.ans.L = Tree.ans.R = 1; Tree.ans.x = Tree.ans.k = Tree.ans.r = Tree.ans.op = 0; int ans; Tree.Query(1, 1, len, qus[i].x); ans = (1LL * (qus[i].x - Tree.ans.x) * power[Tree.ans.k] % mod + Tree.ans.r + save[Tree.ans.R]) % mod; printf("%d\n", ans); } } return 0; }
总结
- 赛时历程:看了眼题,发现题都不太可做。 \(T1\) 不想写类似 luogu P1654 OSU! 维护幂次的一大坨东西, \(T2\) 的暴力可写但分数太低, \(T3\) 口胡出了基环树的做法(但树的假了,反倒拿到了乱搞分), \(T4\) 题意理解有点问题,需要手摸样例。尝试继续想 \(T3\) 的结论无果发现之前基环树的做法是假的,然后恼了,打算先把昨天 \(T3\) 改了再来写这几题的暴力。然后我的键盘就因为前几天 @jijidawang 拉我被键盘线绊倒了,硬生生把 \(USB\) 接口掰弯了,当时以为没事,然后左 Shift 和左 Ctrl 用完之后各有 \(5 \sim 10s\) 内不能使用另一个,导致选中和复制粘贴即为麻烦。以为是电脑问题,把代码传到了 @Charlie_ljk 电脑上,然后就重启了,开机后键盘仍不能用,且 Shift 和 Ctrl 不能一直按,只能手动配 VSCode 设置,还一直显示有 hzoi 用户远程登录要关我机,但我拿终端的
who -u显示只有我自己登录,可能是 \(feifei\) 以为我赛时传递代码作弊(?)。然后索性拿 @Charlie_ljk 电脑写代码了。改完昨天 \(T3\) 并写完今天 \(T2,T3\) 暴力后就看见改成了 \(IOI\) 赛制,然后就去手摸 \(T4\) 样例了,发现之前的修改时刻会对以后的所有修改时刻产生影响,离线下来建时刻线段树维护后缀乘的思路假了,然后就输出了 \(T1,T2,T3\) 的样例,并凭借测评机波动和减小常数让 \(T2\) 多过了 \(2\) 个点。输出完 \(T3\) 大样例后就结束了。
后记
-
总-分-总
-
赛前公告
-
约 \(9:30\) 时赛制改成了 \(IOI\) 赛制,并 适度 提醒做法。

-
赛后题解补充

-
-
组题人写的题面还是很抽象,理解和转化都需要一定时间。
-
题目背景夹带私活。



本文来自博客园,作者:hzoi_Shadow,原文链接:https://www.cnblogs.com/The-Shadow-Dragon/p/18364723,未经允许严禁转载。
版权声明:本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0) 进行许可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号