程序存储问题（贪心算法）

 

 

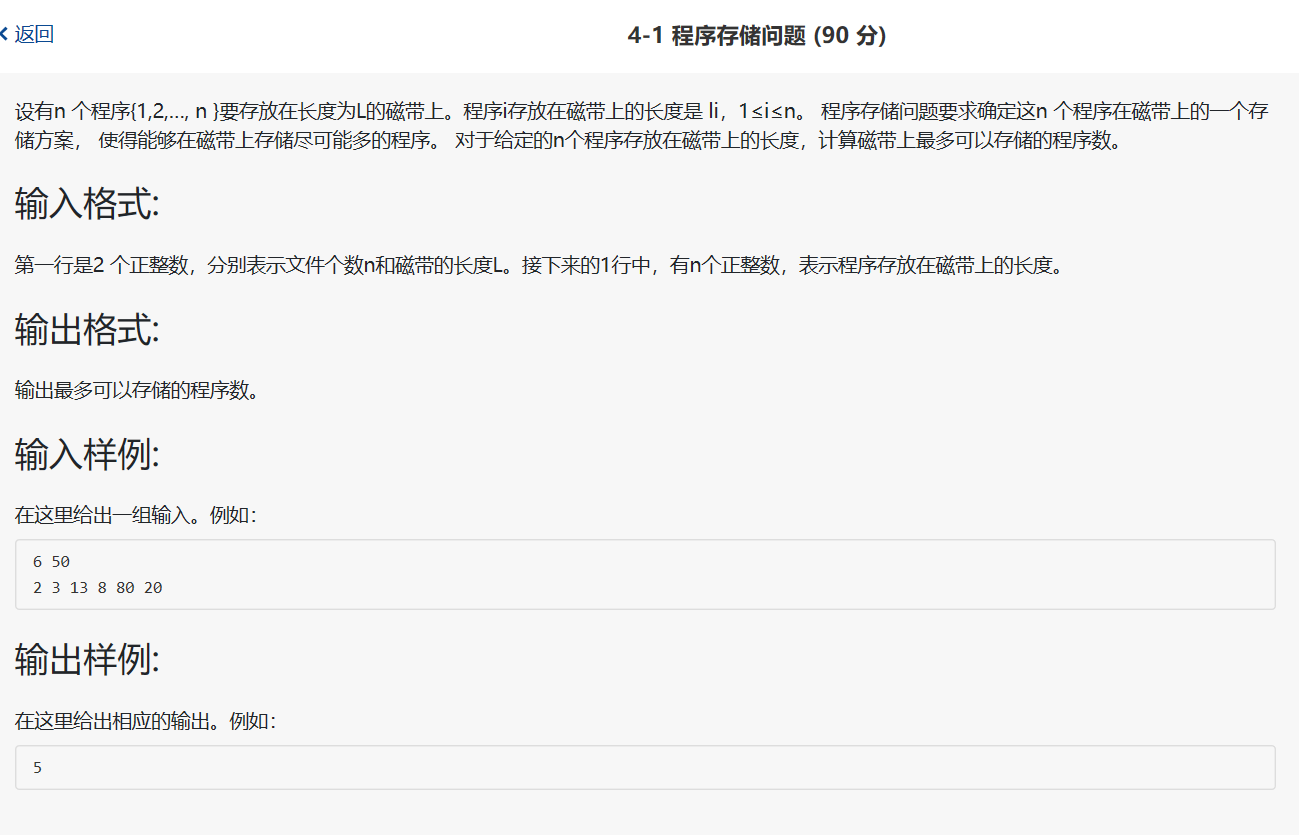
问题描述

条件：磁盘空间有限；程序大小不同。

在有限的磁盘上存放尽可能多的程序，就要求选择的程序尽可能小。

算法描述

贪心算法：总是从可选程序中选择最小的试放入磁盘。

1. 排序：对程序按大小升序排；

2. 循环添加：从i = 1开始，选择排序后序列的第 i 个（即a[i]，1 <= i <= n）个加入暂存（sum，初始为0），判断是否满足sum小于磁盘空间，是则计数（count++），否则跳出循环；

反证法证明贪心选择可以推出最优解：

1. 证明选择可以从贪心（最小程序）开始：选择从最小程序开始即解不为空时可以选择最小程序。假设解不为空，从这样得到的选择序列中任选一个，用最小程序替换，放入程序数（count）不变；

2. 证明最优子结构性质：在解不为空、第一次可以选择最小程序的前提下，假设在最优解中去掉第一次选择的最小程序后得到的子问题的最优解的count_0大于原问题最优解的count_1-1，那么将最小程序加入选择产生的解的count_2大于count_1，此时count_1不是最优解，这不成立。故此问题具有最优子结构性质。

时间和空间复杂度分析

时间复杂度：程序进行了一次快排（O(nlogn)）和循环（O(n)），故时间复杂度为O(nlogn)；

空间复杂度：程序new了一个一维数组（a[n]）用于存放每个程序的大小，故时间复杂度为O(n)。

心得体会

虽然参考会场安排问题的证明大致写了以上证明，但我对贪心算法的正确性的证明还是有很大的疑惑。