题解 P4299 首都

$\text{Link}$

一个 LCT + 二分查找重心的做法。

题意

给定一个森林，支持以下操作：

• A x y：连接 $x,y$。
• Q x：查询点 $x$ 所在树的重心。
• Xor：查询所有树的重心编号的异或和。

简化版题意：动态维护树重心。

题解

对于节点 $x$，维护 $siz_x$ 和 $tot_x$，分别表示 $x$ 总子树大小（包括虚边所连的节点）和 $x$ 的虚儿子个数（认父不认子）。

对于连边操作，直接调用 LCT 的 $link$ 操作即可，但为了维护上面两个量，可以先 $split$ 后再更新。

维护重心需要两个性质：

1. 以重心为根的最大的子树节点数小于总节点数的一半。

2. 连接两棵树后，新的重心必定在两棵树原重心的路径上。

两个性质都可用反证法证，令 $csiz_u$ 表示点 $u$ 最大子树的大小。

对于性质 1，若 $csiz_u$ 大于所有节点数的一半，则存在这颗子树中的一点 $v$，$csiz_v<cisz_u$，所以重心必不是 $u$，假设不成立，性质 1 得证（这个很好理解，画图就看得出来）。

对于性质 2，设点 $u,v$ 为原两棵树的重心，两棵树的大小分别为 $sum_u,sum_v$， 若点 $x$ 在 $u$ 所在的树上且不在 $u$ 到 $v$ 的路径上，那么新增了一棵子树，必会让 $csiz_x$ 增加 $sum_v$，又因为性质 1，原先 $csiz_x>\frac{sum_u}{2}$，所以连接另一棵树后 $csiz_x>\frac{sum_u+sum_v}{2}$，由性质 1 知 $x$ 不是新树的重心，假设不成立，性质 2 得证。

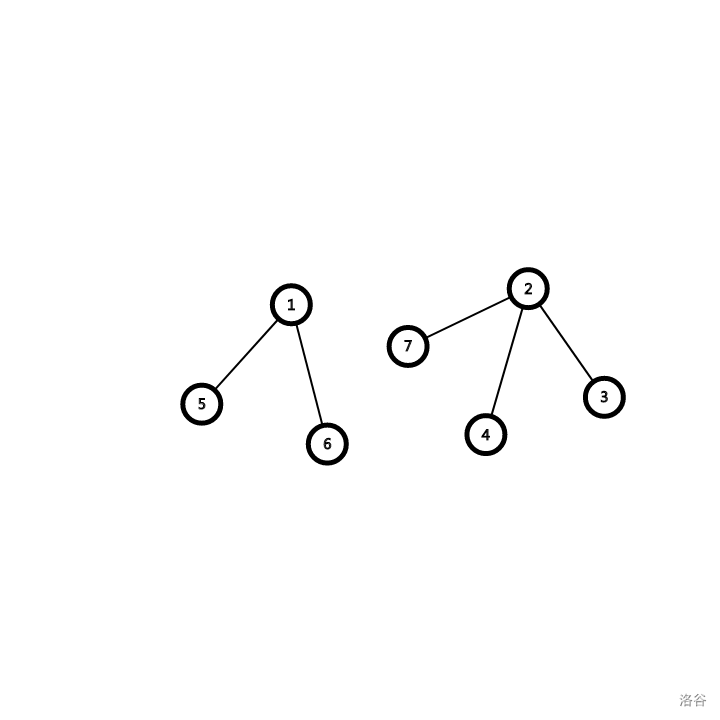
如图，两棵树重心分别是 $1$ 和 $2$。

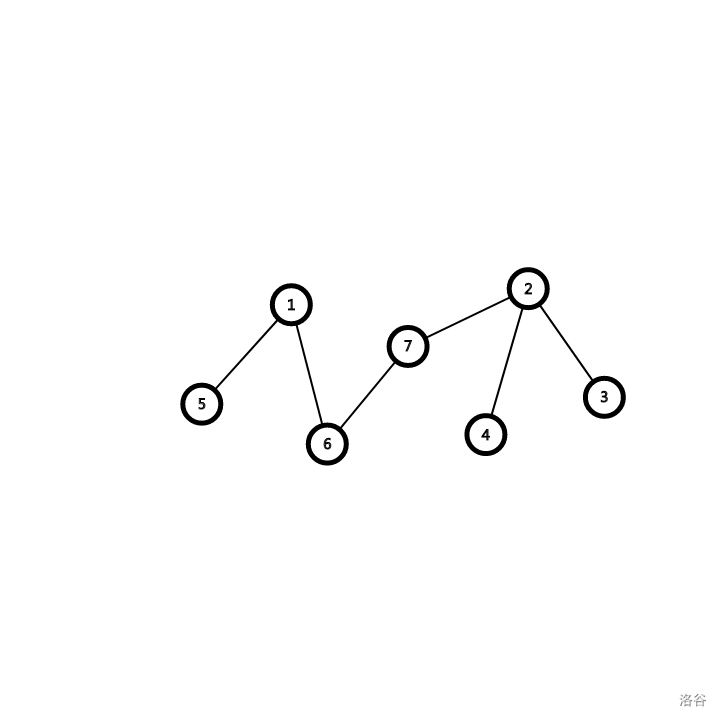
连接 $6,7$ 后，对于不在两树重心上的 $5$ 和 $3$，他们最大子树节点数必定增加，便不可能是重心。

为了方便处理，用重心来代表一棵树，再用并查集维护，每个点的并查集存所在树的重心，连边后就把原来两棵树重心 $split$ 成一条链。对于链上的点 $u$，会把链分为两部分，用 $lsum,rsum$ 维护 $u$ 左右两边的子树和。然后根据比较左右儿子 $lsum$ 和 $rsum$ 的大小，选择子树较大的儿子，直到满足性质 1，再 $splay(u)$ 保证复杂度。

需要注意，当树的大小为奇数时，只有一个重心，树的大小为偶数时可能会有多个重心，要找序号最小的。

具体细节看代码叭。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct Link_Cut_Tree {
    struct node {
        int fa, ch[2], siz, tot;
        bool tag;
    } t[N];
    bool nroot(int x) { return t[t[x].fa].ch[0] == x || t[t[x].fa].ch[1] == x; }
    void pushup(int x) { t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + 1 + t[x].tot; }
    void pushr(int x) {
        swap(t[x].ch[0], t[x].ch[1]);
        t[x].tag ^= 1;
    }
    void pushdown(int x) {
        if(!t[x].tag) return;
        if(t[x].ch[0]) pushr(t[x].ch[0]);
        if(t[x].ch[1]) pushr(t[x].ch[1]);
        t[x].tag = 0;
    }
    void pushdown_path(int x) {
        if(nroot(x))
            pushdown_path(t[x].fa);
        pushdown(x);
    }
    void rotate(int x) {
        int y = t[x].fa, z = t[y].fa, ych = t[y].ch[1] == x, w = t[x].ch[!ych];
        if(nroot(y)) t[z].ch[t[z].ch[1] == y] = x;
        t[x].ch[!ych] = y, t[y].ch[ych] = w;
        if(w) t[w].fa = y;
        t[y].fa = x, t[x].fa = z;
        pushup(y);
    }
    void splay(int x) {
        pushdown_path(x);
        int y;
        while(nroot(x)) {
            y = t[x].fa;
            if(nroot(y))
                rotate(t[y].ch[1] == x ^ t[t[y].fa].ch[1] == y ? x : y);
            rotate(x);
        }
        pushup(x);
    }
    void access(int x) {
        for(int y = 0; x; x = t[y = x].fa)
            splay(x), t[x].tot += t[t[x].ch[1]].siz - t[y].siz, t[x].ch[1] = y, pushup(x);
    }
    void makeroot(int x) {
        access(x);
        splay(x);
        pushr(x);
    }
    int findroot(int x) {
        access(x);
        splay(x);
        while(t[x].ch[0]) pushdown(x), x = t[x].ch[0];
        splay(x);
        return x;
    }
    void split(int x, int y) {
        makeroot(x);
        access(y);
        splay(y);
    }
    void link(int x, int y) {
        split(x, y);
        t[t[x].fa = y].tot += t[x].siz;
        pushup(y);
    }
    int dfs(int x) {
        int lsum = 0, rsum = 0, sum = t[x].siz >> 1, bre = t[x].siz & 1, u = 1e9, curl, curr;
        for(;x;) {
            pushdown(x);
            curl = lsum + t[t[x].ch[0]].siz;
            curr = rsum + t[t[x].ch[1]].siz;
            if(curl <= sum && curr <= sum) {
                if(bre) {
                    u = x;
                    break;
                }
                u = min(u, x);
            }
            if(curl < curr) {
                lsum += t[t[x].ch[0]].siz + t[x].tot + 1;
                x = t[x].ch[1];
            }
            else {
                rsum += t[t[x].ch[1]].siz + t[x].tot + 1;
                x = t[x].ch[0];
            }
        }
        splay(u);
        return u;
    }
} LCT;
int n, m;
int fa[N], ans;
int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
        fa[i] = i, ans ^= i;
    char op[3];
    int x, y;
    while(m--) {
        scanf("%s", op);
        if(op[0] == 'A') {
            scanf("%d%d", &x, &y);
            LCT.link(x, y);
            x = find(x), y = find(y);
            LCT.split(x, y);
            int g = LCT.dfs(y);
            ans ^= x ^ y ^ g;
            fa[x] = fa[y] = fa[g] = g;
        }
        else if(op[0] == 'Q') {
            scanf("%d", &x);
            printf("%d\n", find(x));
        }
        else printf("%d\n", ans);
    }
    return 0;
}

这道题挺难理解的，最好是自己可以画画图。