基础数论

数论


前排提示

仍在更新与修改

本文适合对数学和计算机都有了解的人来阅读（实际上是博主的备忘录orz）

且本博客只有一些基础内容

补充：

2025-4-30：也终于快完工了，写了一个星期了QAQ

参考资料:

[1]初等数论(闵嗣鹤、严士健)笔记目录

[2]基础数论学习笔记

[3]oiwiki 数论

[4] 算法竞赛专题解析（罗勇军的博客）

[5]Algorithms for Competitive Programming

[6]数学奥林匹克小丛书数学卷 6

[7]初等数论（张秀平老师） 北师大 高清1080p版（全集)

[8]数论--同余方程

[9]反演入门学习笔记


目录

目录


前置定义

整除

定义：设 \(a, b \in \mathbb{Z}\)，\(a \neq 0\)。如果存在 \(q \in \mathbb{Z}\)，使得 \(b = aq\)，那么就说 \(b\) 可被 \(a\) 整除，记作 \(a \mid b\);

\(b\) 不被 \(a\) 整除记作 \(a \nmid b\)。

如果\(a\mid b\)，则称\(a\)为\(b\)的因数，\(b\)为\(a\)的倍数。

符合一些简单的性质:与正负无关，传递性，对于线性组合仍成立

常用的有

1.\(a \mid b \land b \mid a \iff a=\pm b\)

2.设 $ b \neq 0 $，那么 $ a \mid b \implies |a| \leq |b| $。

3.设 \(a \neq 0\)，\(b = qa + c\)，那么 \(a \mid b \iff a \mid c\)。

4.构造线性组合证明整除成立

5.通过性质4，构造\(x|yz \land y<x \land z<x\)后,由性质2得到\(x\)是合数(见下文)


素数和合数

定义:素数是因数最少的数

​ 素数（prime）是一个大于1的正整数，且不能被1和其本身外的任何正整数整除。

​ 若一个大于 的正整数不是素数，则是合数（composite）

如果没有特别说明，素数总是指正的素数。合数同理。

  • 对于合数 $ a $，一定存在素数 $ p \leq \sqrt{a} $ 使得 $ p \mid a $。
  • 素数有无穷多个。
  • 所有大于 3 的素数都可以表示为 $ 6n \pm 1 $ 的形式。

算术基本引理
设 \(p\) 是素数，$p \mid a_1a_2 $，那么 $ p \mid a_1 $ 和 $ p \mid a_2$ 至少有一个成立。

算术基本引理是素数的本质属性，也是素数的真正定义。


算术基本定理（唯一分解定理）

设正整数 $ a $，那么必有表示： $ a = p_1p_2 \cdots p_s $ 其中 $ p_j (1 \leq j \leq s) $ 是素数。并且在不计次序的意义下，该表示唯一。

假设 $$ a = p_1^{e_1} \cdots p_k^{e_k}, \quad b = p_1^{f_1} \cdots p_k^{f_k}, \quad e_i, f_i \geq 0 $$

那么就有

\[ab = p_1^{e_1 + f_1} \cdots p_k^{e_k + f_k} \]

\[\frac{a}{b} = p_1^{e_1 - f_1} \cdots p_k^{e_k - f_k} \quad \text{if } b \mid a \]

\[a^m = p_1^{me_1} \cdots p_k^{me_k} \]

\[(a, b) = p_1^{\min(e_1, f_1)} \cdots p_k^{\min(e_k, f_k)} \]

\[\text{lcm}(a, b) = p_1^{\max(e_1, f_1)} \cdots p_k^{\max(e_k, f_k)} \]

算法知识请见素数


约数（因数）

定义：若 \(a \mid b\)，则称 \(b\) 是 \(a\) 的 倍数，\(a\) 是 \(b\) 的 约数。

​ 若\(d \mid a \land d \mid b\)，则称\(d\)是\(a,b\)的公因数。

0 是所有非 0 整数的倍数。对于整数 \(b \neq 0\)，\(b\) 的约数只有有限个。

平凡约数（平凡因数）：对于整数 \(b \neq 0\)，\(\pm 1\)、\(\pm b\) 是 \(b\) 的平凡约数。当 \(b = \pm 1\) 时，\(b\) 只有两个平凡约数。

对于整数 \(b \neq 0\)，\(b\) 的其他约数称为真约数（真因数、非平凡约数、非平凡因数）。

在具体问题中，如果没有特别说明，约数总是指正约数。

算法知识见质因数


带余数除法

定义： 设 \(a, b\) 是两个整数，\(a \neq 0\)，则存在唯一的一对整数 \(q\) 和 \(r\)，满足

\[b = aq + r, \quad 0 \leq r < |a| \]

其中 \(q\) 称为 \(b\) 除以 \(a\) 所得的商，\(r\) 称为 \(b\) 除以 \(a\) 所得的余数。

证明该定理比较重要:

​ 1.第一个观察是任意整数必然掉在一个起始数为整数，并且长度为b的区间里，从而证明了存在性。

​ 2.证明唯一性的常用手段：假设存在另外一组数字同样满足条件，最后证明若想条件满足，只能使得,从而证明唯一性。

用来证明整除问题


基数

令 \(b\) 为一个正整数，且 \(b > 1\)（这说明是以 \(b\) 为基 (base \(b\))）。则所有正整数 \(n\) 可以被唯一地写为下面的形式 $ n = a_k b^k + a_{k-1} b^{k-1} + \ldots + a_1 b + a_0 \tag{2.1} $ 其中 \(k\) 为非负整数，\(a_j\) 为整数满足 \(0 \leq a_j \leq b - 1\) 对于 \(j = 0, 1, \ldots, k\)，且 \(a_k \neq 0\)。


GCD/LCM

判断最大公约数

令 \(a, b\) 为不同时为 0 的整数，则正整数 \(d\) 是 \((a, b)\) 当且仅当:

  1. \(d \mid a\) 且 \(d \mid b\)
  2. 若 \(c\) 为满足 \(c \mid a, c \mid b\) 的整数，则 \(c \mid d\)

并且可以得到\((\frac ad, \frac bd)=1\)

若 \((a, b) = 1\) 则整数 \(a, b\) 互质/互素（relatively prime, coprime），也就是说，他们的最大公约数为 1。

  • 0只与1互质，0与其他非1整数均不互质。

算法知识请见GCD


数论函数

若函数 $ f(n) $ 满足 $ f(1) = 1 $，且 $ f(xy) = f(x)f(y) $ 对任意互质的 $ x, y \in \mathbb{N}^* $ 都成立，则 $ f(n) $ 为 积性函数。

若函数 $ f(n) $ 满足 $ f(1) = 1 $ 且 $ f(xy) = f(x)f(y) $ 对任意的 $ x, y \in \mathbb{N}^* $ 都成立，则 $ f(n) $ 为 完全积性函数。

  • 积性函数可以根据其质因数分解来计算，即如果 \(n = p_1^{k_1} \cdot p_2^{k_2} \cdots p_m^{k_m}\)，那么可以按每个质因数分别计算函数值再相乘得到 \(f(n)\)。

若函数\(f(n)\)满足\(f(1)=0\)且\(f(xy)=f(x)+f(y)\)对任意互质的\(x,y\in\mathbb{N}^*\)都成立，则\(f(n)\)为加性函数。

若函数\(f(n)\)满足\(f(1)=0\)且\(f(xy)=f(x)+f(y)\)对任意的\(x,y\in\mathbb{N}^*\)都成立，则\(f(n)\)为完全加性函数。

  • 加性函数可以根据其质因数分解来计算，即如果 \(n = p_1^{k_1} \cdot p_2^{k_2} \cdots p_m^{k_m}\)，那么可以按每个质因数分别计算函数值再相加得到 \(f(n)\)。

常见的积性函数有：

  • 单位元函数\(\varepsilon(n):=[n=1]\)

  • 幂函数\(\operatorname{Id}_k(n):=n^k\).当\(k=1\)时为恒等函数\(\operatorname{Id}(n)\),当\(k=0\)时为常数函数\(1(n)\)

  • 除数函数\(\sigma_k(n):=\sum_{d|n}d^k\),当\(k=1\)时为因数和函数\(\sigma(n)\),当\(k=0\)时为因数个数函数\(\sigma_0(n)\)

  • 常数函数\(\textbf{1} (x)=1\)

所有积性函数都能被线性筛求解


狄利克雷卷积

定义狄利克雷卷积\(*\)为\((f*g)(n)=\sum_{d|n}f(d)g\left(\frac{n}{d}\right)\)

其满足交换律、结合律、分配律（证略）

可以得到一下关系

\(\varphi*1=\operatorname{Id}\)，\(\operatorname{Id}_k*1=\sigma_k\)，\(\textbf{1} * \mu = \varepsilon\)

狄利克雷逆

若\(f*f^{-1}=\varepsilon\)，则\(f^{−1}\)被称为 $f $的狄利克雷逆（狄利克雷卷积的逆元）

由\(\textbf{1} * \mu = \varepsilon\)，\(\mu\) 是 \(\textbf{1}\) 的逆元



同余类与剩余系

同余类

定理1： 若 $ m $ 是一个给定的正整数，则全部整数可分成 $ m $ 个集合，记作 $ K_0, K_1, \cdots, K_{m-1} $，其中 $ K_r (r = 0, 1, \cdots, m - 1) $ 是由一切形如 $ qm + r (q = 0, \pm 1, \pm 2 \cdots) $ 的整数所组成的。

这些集合具有下列性质： (i) 每一整数 必包含在而且仅在 上述的一个集合里面， (ii) 两个整数同在一个集合的充分与必要条件是这两个整数对模 $ m $ 同余。

定理 1 中的 $ K_0, K_1, \cdots, K_{m-1} $ 叫做模 $ m $ 的 同余类。一个剩余类中任一数叫做它同类的数的剩余。

我们把模\(m\)的同余类全体构成的集合记为\(\mathbb{Z}_m\),即 \(\mathbb{Z}_m:=\{r\bmod m:0\leq r<m\}\)

由商群的定义可知\(\mathbb{Z}_m=\mathbb{Z}/m\mathbb{Z}\),所以有时我们也会用\(\mathbb{Z}/m\mathbb{Z}\)表示\(\mathbb{Z}_m\)。


完全剩余系

若 $ a_0, a_1, \cdots, a_{m-1} $ 是 $ m $ 个整数，并且其中任何两数都不同在一个剩余类里，则 $ a_0, \cdots, a_{m-1} $ 叫做模 $ m $ 的一个 完全剩余系。

易知：

  • 完全剩余系两两对模 $ m $ 不同余。

    • 连续的m个整数构成m的一个完全剩余系。其中必有一个数是m的倍数。
    • 若\((a,m)=1\),一个集合 $ x = {a_0, a_1, \ldots, a_{m-1}} $ 是 $ m $ 的一个完全剩余系，那么集合 $ {y \mid y = at + b, t \in x} $（其中 $ (a, m) = 1 $）也是 $ m $ 的一个完全剩余系。

    这一点很重要，可以用来解同余不等式，例如icpc沈阳2020I

    • 若\((m_1,m_2)=1\),\(x_1\)是\(m_1\)的一个完全剩余系，\(x_2\)是\(m_2\)的一个完全剩余系，则\(x_1m_2+x_2m_1\)是\(m_1m_2\)的一个完全剩余系

  • 最小非负（完全）剩余系：\(0,\ldots,m-1\);

  • 最小正（完全）剩余系：\(1,\ldots,m\);

  • 绝对最小（完全）剩余系：\(-\lfloor m/2\rfloor,\ldots,-\lceil-m/2\rceil-1\);

  • 最大非正（完全）剩余系：\(-m+1,\ldots,0\);

  • 最大负（完全）剩余系：\(-m,\ldots,-1\)。

若无特殊说明，一般我们只用最小非负剩余系。

既约同余类

发现在模\(m\)的任意一个同余类中，任取两个整数\(a_1,a_2\)均有\((a_1,m)=(a_2,m)\)。得到：

定义 如果一个模\(m\)的剩余类里面的数均与\(m\)互质， 则称其为既约同余类 或 既约剩余类。其个数为\(\varphi(m)\)

简化剩余系

在与模\(m\)互质的全部剩余类中,从每一类各任取一数所作成的数的集合,叫做模\(m\)的一个简化剩余系（既约剩余系）。

我们可以将完全剩余系简称为完系，将简化剩余系称为缩系。

  • 若\((m_1,m_2)=1\),\(x_1\)是\(m_1\)的一个完全剩余系，\(x_2\)是\(m_2\)的一个完全剩余系，则\(x_1m_2+x_2m_1\)是\(m_1m_2\)的一个完全剩余系

类似地，我们也可以定义最小非负既约剩余系等概念。

若无特殊说明，一般我们只用最小非负既约剩余系。

Tip

1.icpc沈阳2020I 利用完全剩余系的性质求解不等式组，注意互质定理才能成立。



阶和原根

阶

由欧拉定理可知，对 \(a \in \mathbb{Z}\)，\(m \in \mathbb{N}^*\)，若 \((a, m) = 1\)，则 $ a^{\varphi(m)} \equiv 1 \pmod{m}. $

因此满足同余式 \(a^n \equiv 1 \pmod{m}\) 的最小正整数 \(n\) 存在，这个 \(n\) 称作 \(a\) 模 \(m\) 的阶，记作 \(\delta_m(a)\) 或 \(\mathrm{ord}_m(a)\)

性质1: \(a, a^2, \cdots, a^{\delta_m(a)}\) 模 \(m\) 两两不同余

性质2: 若\(a^n \equiv 1 \pmod{m}\)，则 \(\delta_m(a) \mid n\)

推导：\(If\ a^p \equiv a^q \pmod{m}\)，\(then\ p \equiv q \pmod{\delta_m(a)}\)。 （费马扩展的原定理）

​ $If\ (a,p)=1,then\ \delta_p(a) \mid \varphi(p) $

性质3: \(If\ m \in \mathbb{N}^*\)，\(a, b \in \mathbb{Z}\)，\((a, m) = (b, m) = 1\)，

​ $then\ \delta_m(ab) = \delta_m(a) \delta_m(b) $ \(\iff\)$ (\delta_m(a), \delta_m(b)) = 1 $

性质4: 设 \(k \in \mathbb{N}\) ，\(m \in \mathbb{N}^*\)，\(a \in \mathbb{Z}\)，\((a, m) = 1\)，则 \(\delta_m(a^k) = \frac{\delta_m(a)}{(\delta_m(a), k)}\)

原根

设 \(m \in \mathbb{N}^*\)，\(g \in \mathbb{Z}\)。若 \((g, m) = 1\)，且 \(\delta_m(g) = \varphi(m)\)，则称 \(g\) 为模 \(m\) 的原根。

即 $ g $ 满足 \(\delta_m(g) = |\mathbb{Z}_m^*| = \varphi(m)\)。

由阶的性质1易知\(g,g^2,...,g^{\varphi(m)}\)构成\(m\)的简化剩余系。
一个数\(m\)的最小原根不大于\(m^{0.25}\)


原根判定定理

设\(m\geqslant 3,(g,m)=1\),则:\(g\)是模\(m\)的原根\(\iff\)对于\(\varphi(m)\)的每个素因数\(p\),都有\(g^{\frac{\varphi(m)}{p}}\not\equiv 1\pmod{m}\).


原根个数

若一个数\(m\)有原根\(g\),那么对于任意\(\varphi(m)\)的因子\(d\),模\(m\)的\(d\)阶元素存在且个数为\(\varphi(d)\)。 特别地，\(m\)的原根个数为\(\varphi(\varphi(m))\)。
假如找到了一个原根\(g\),不难证明对于所有\(\gcd(x,\varphi(m))=1\)的\(x\),\(g^x\)均为原根，所以模\(m\)的原根有\(\varphi(\varphi(m))\)个


原根存在定理

一个数\(m\)存在原根当且仅当\(m=2,4,p^\alpha,2p^\alpha\),其中\(p\)为奇素数,\(\alpha\in\mathbb{N}^*\).

而且暴力找一个数的原根是\(O(logn)\)的，可以接受。


求原根
通过以上性质，我们可以想出一个求原根的算法：

由存在定理，预处理出所有有原根的数;

再通过判定定理找出最小原根g；

通过个数的性质得到soyo解。
算法略，原根



离散对数

取有原根的正整数模数\(m\),设其一个原根为\(g\).

对满足\((a,m)=1\)的整数\(a\),我们知道必存在唯一的整数\(0\leq k<\varphi(m)\)使得 \(g^k\equiv a\pmod{m}\)

我们称这个\(k\)为以\(g\)为底，模\(m\)的离散对数，记作\(k=\operatorname{ind}_ga\),在不引起混淆的情况下可记作\(\operatorname{ind}a\). 显然\(\operatorname{ind}_g1=0,\operatorname{ind}_gg=1\).

经典问题

解决离散对数问题一般要用到大步小步算法
\(a^x\equiv b\pmod{m}\)可以直接用exBSGS算法解决，而 \(x^a\equiv b\pmod{m}\)将需要转化成BSGS的模型：
我们令\(x=g^c\),\(g\)是\(p\)的原根,问题转化为求解\((g^c)^a\equiv b\pmod{p}\)

即 \((g^a)^c\equiv b\pmod{p}\)

于是就转换成了BSGS的基本模型了，可以在\(O(\sqrt{p})\)解出\(c\),这样可以得到原方程的一个特解\(x_0\equiv g^c\pmod{p}\).

或者\(b=g^t\)两边取离散对数变成\(ca \equiv t(mod\ \varphi(p))\)的不定方程割到解

在知道\(x_0\equiv g^c\pmod{p}\)的情况下，我们想得到原问题的所有解。首先我们知道\(g^{\varphi(p)}\equiv 1\pmod{p}\),于是可以得到 \(\forall t\in\mathbb{Z},x^a\equiv g^{c\cdot a+t\cdot\varphi(p)}\equiv b\pmod{p}\) 于是得到所有解为 \(\forall t\in\mathbb{Z},a|t\cdot\varphi(p),x\equiv g^{c+\frac{t\cdot\varphi(p)}{a}}\pmod{p}\) 对于上面这个式子，显然有\(\frac{a}{(a,\varphi(p))}|t\).因此我们设\(t=\frac{a}{(a,\varphi(p))}\cdot i\),得到 \(\forall i\in\mathbb{Z},x\equiv g^{c+\frac{\varphi(p)}{(a,\varphi(p))}\cdot i}\pmod{p}\) 这就是原问题的所有解。




素数

素数计数函数：小于或等于 $ x $ 的素数的个数，用 $ \pi(x) $ 表示。随着 $ x $ 的增大，有这样的近似结果： $ \pi(x) \sim \frac{x}{\ln(x)} $

​ 「Meissel–Lehmer 算法」是一种能在亚线性时间复杂度内求出 1\sim n 内质数个数的一种算法。

这里给出论文原文

下面给出简化版代码

constexpr int N = 8e6+5,MI = 1.8e6,MJ = 60;
int f[MI+5][MJ+5];
int primes[N/10],g[N],cnt=0;
bitset<N>nop;

void init(){
    for(int i=2;i<N;i++){
        if(nop[i]==0)primes[++cnt]=i;
        for(int j=1;j<=cnt;j++){
            if(primes[j]*i>=N)break;
            nop[i*primes[j]]=1;
            if(i%primes[j]==0)break;
        }
    }
    // 警惕！这里的 g 数组表示的 pi(n) 含有 1，是 pi(n)+1
    for(int i=1;i<N;i++)g[i]=g[i-1]+!nop[i];                                
    for(int i=1;i<=MI;i++)f[i][0]=i;
    for(int i=1;i<=MI;i++)          
        for(int j=1;j<=MJ;j++)
            f[i][j] = f[i][j-1]-f[i/primes[j]][j-1];
}

ll dp(ll i, ll j){
    if(i<=MI && j<=MJ)return f[i][j];
    if(!i||!j)return i;
    if(i < N && 1ll * primes[j]* primes[j] >= i)return max(0ll,g[i]-j);
    return dp(i,j-1)-dp(i/primes[j],j-1);
}

ll pi(ll n){
    if(n<N)return g[n]-1;
    ll sn =pow(n,1.0/3);
    ll m = g[sn]-1;
    ll res = dp(n,m)+m-1;
    m++;
    for(;1ll*primes[m]*primes[m]<=n;m++)
        res-=pi(n/primes[m])-pi(primes[m])+1;
    return res;
}
void solve(){
    ll n;cin>>n;
    cout<<pi(n);
}

确定性素数测试:试除法、Lucas–Lehmer 测试（比较难，不做介绍）和椭圆曲线素性证明。

概率性素数测试（基于费马小定理）:Miller-Rabin素数检测

​ 二次探测定理：如果 p 是奇素数，则 \(x^2≡1(mod\ p)\) 的解为$ x≡1 $或 \(x≡p−1(mod\ p)\) 。

大数用java自带的函数isProbablePrime()判断，它的内部实现用到了Miller-Rabin测试和Lucas-Lehmer测试。

import java.math.*;
import java.util.*;
public class Main {
    public static void main(String[] args){
        Scanner in = new Scanner (System.in);
        BigInteger a;
        while(in.hasNextBigInteger()){
            a = in.nextBigInteger();
            if(a.isProbablePrime(1))
                System.out.println("Yes");
            else
                System.out.println("No");
        }
    }
}

筛法

求小于等于\(n\)有多少个质数，一般用筛法求解

埃氏筛：从小到大考虑每个数，同时把当前这个数的所有（比自己大的）倍数记为合数，那么运行结束的时候没有被标记的数就是素数了。显然只要对不超过\(\sqrt n\)的数进行筛选。

//参考OIwiki
//O(nloglogn)
const int N = 1e8 + 5;
int prime_cnt = 0;
int primes[N >> 3];
bitset<N> is_prime;

inline void sieve(int n) {
    is_prime.set();
    for (int i = 3; i * i < n; i += 2)
        if (is_prime[i])
            for (int j = i * i; j < n; j += 2 * i)
                is_prime[j] = false;
    primes[prime_cnt++] = 2;
    for (int i = 3; i < n; i += 2)
        if (is_prime[i]) primes[prime_cnt++] = i;
}

优化：只筛选奇数, 分块筛选（内存）优化

//来源于oiwiki
int count_primes(int n) {
  constexpr static int S = 10000;
  vector<int> primes;
  int nsqrt = sqrt(n);
  vector<char> is_prime(nsqrt + 1, true);
  for (int i = 2; i <= nsqrt; i++) {
    if (is_prime[i]) {
      primes.push_back(i);
      for (int j = i * i; j <= nsqrt; j += i) is_prime[j] = false;
    }
  }
  int result = 0;
  vector<char> block(S);
  for (int k = 0; k * S <= n; k++) {
    fill(block.begin(), block.end(), true);
    int start = k * S;
    for (int p : primes) {
      int start_idx = (start + p - 1) / p;
      int j = max(start_idx, p) * p - start;
      for (; j < S; j += p) block[j] = false;
    }
    if (k == 0) block[0] = block[1] = false;
    for (int i = 0; i < S && start + i <= n; i++) {
      if (block[i]) result++;
    }
  }
  return result;
}

区间筛：用于区间大小可以处理的情况，R可以很大（\(10^{16}\)）

代码如下

//生成函数版
vector<char> segmentedSieve(long long L, long long R) {
    // generate all primes up to sqrt(R)
    long long lim = sqrt(R);
    vector<char> mark(lim + 1, false);
    vector<long long> primes;
    for (long long i = 2; i <= lim; ++i) {
        if (!mark[i]) {
            primes.emplace_back(i);
            for (long long j = i * i; j <= lim; j += i)
                mark[j] = true;
        }
    }

    vector<char> isPrime(R - L + 1, true);
    for (long long i : primes)
        for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
            isPrime[j - L] = false;
    if (L == 1)
        isPrime[0] = false;
    return isPrime;
}

//区间埃氏筛,没有pre-generate版
vector<char> segmentedSieveNoPreGen(long long L, long long R) {
    vector<char> isPrime(R - L + 1, true);
    long long lim = sqrt(R);
    for (long long i = 2; i <= lim; ++i)
        for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
            isPrime[j - L] = false;
    if (L == 1)
        isPrime[0] = false;
    return isPrime;
}

一些性质：

狄利克雷定理 (Dirichlet's Theorem) 若 \(a, b\) 为不会被同一个素数整除的两个正整数，则 \(an + b, n = 1, 2, 3, \ldots\) 这个等差数列中有无限多个素数。

对于任意正整数n，存在至少n个连续的正合数。

对任意给定的正整数n > 1，存在一个素数p，使得n < p < 2n。


Tips

暂无，博主做题太少了ORZ。


Carmichael函数

对正整数\(n\),定义Carmichael函数为对任意满足\((a,n)=1\)的整数\(a\),使 \(a^m\equiv 1\pmod{n}\) 恒成立的最小正整数\(m\)。

即: \(\lambda(n)=\max\{\delta_n(a):(a,n)=1\}\)

Carmichael函数有如下性质:

  1. (Carmichael定理)对任意素数\(p\)和任意正整数\(r\), \(\lambda(p^r)=\begin{cases}\frac{1}{2}\varphi(p^r),&p=2\land r\geq 3,\\\varphi(p^r),&\text{otherwise}.\end{cases}\)

a. 对任意正整数\(n\),有\(\lambda(n)|\varphi(n)\)

b. 对任意正整数\(a,b\),有\(a|b\Longrightarrow\lambda(a)|\lambda(b)\)

  1. 令\(n\)的唯一分解式为\(n=\prod_{i=1}^{k}p_i^{r_i}\),则\(\lambda(n)=\left[\lambda(p_1^{r_1}),\lambda(p_2^{r_2}),\ldots,\lambda(p_k^{r_k})\right]\)

由中国剩余定理和Carmichael定理易证。

进而有对任意正整数\(a,b\),有\(\lambda([a,b])=[\lambda(a),\lambda(b)]\)


Carmichael数

对于合数\(n\)，如果对于所有与n互质的正整数b，都有同余式\(b^{n-1} \equiv 1 (mod\ n)\)成立，则称合数\(n\)为Carmichael数

判别法：

合数 $ n $ 是 Carmichael 数当且仅当 $ n $ 无平方因子且对 $ n $ 的任意质因子 $ p $ 均有 $ p - 1 \mid n - 1 $。

或 合数 $ n $ 是 Carmichael 数当且仅当 $ \lambda(n) \mid n - 1 $，其中 $ \lambda(n) $ 为 Carmichael 函数。

两者等价。

Carmichael数有如下性质:

  1. Carmichael数无平方因子且至少有3个不同的质因子。
  2. 设\(C(n)\)为小于\(n\)的Carmichael数个数,则:
  • (Alford, Granville, Pomerance. 1994) \(C(n)>n^{2/7}\)。

​ 由此可知Carmichael数有无限多个。

  • (Erdős. 1956) \(C(n)<n\exp\left(-c\frac{\ln n\ln\ln\ln n}{\ln\ln n}\right)\),其中\(c\)为常数。

    由此可知Carmichael数的分布十分稀疏。实际上\(C(10^9)=646\),\(C(10^{18})=1401644\)。


反素数

本身没用，但结论与思考方式有用

对于某个正整数 \(n\)，如果任何小于\(n\)的正数的约数个数都小于\(n\)的约数个数，则称为是 反素数

  1. 反素数肯定是从2开始的连续素数的幂次形式的乘积。

  2. 数值小的素数的幂次大于等于数值大的素数，即 $ n = p_1^{k_1} p_2^{k_2} \cdots p_n^{k_n} $ 中，有 $ k_1 \geq k_2 \geq k_3 \geq \cdots \geq k_n $。

    从而用dfs寻找



质因数

根据唯一分解定理，所有正整数都有唯一一种质数表达形式。然而应该怎么求？

试除法

算法复杂度：\(O(\sqrt n)\)，所以一般用不上

思路简单，略

vector<int> p[10000];  //p[]记录质因子
vector<int> c[10000];  //c[i]记录第i个质因子的个数

void fun(int n){
    int m = 0;
    for(int i=2; i*i<=n; i++)
        if(n%i== 0){
           p[++m] = i, c[m] = 0;
           while(n%i == 0)            //记录次数
              n/=i, c[m]++;    
        }
    if(n>1)                           //特判自身
       p[++m] = n, c[m] = 1;  
}

筛法+试除法

算法复杂度：\(O(\sqrt {\frac{n}{ln(n)} })\)，数据给的小用这个

代码略，拼接即可


Pollard_rho算法

见算法中Pollard_rho算法


Tips

  1. 在\(n!\)的标准分解式中质因数\(p(p\leq n)\)的指数\(h=\left[\frac{n}{p}\right]+\left[\frac{n}{p^2}\right]+\cdots=\sum_{r=1}^\infty\left[\frac{n}{p^r}\right]\).

​ 证明略(用取整函数能证明)，



GCD

辗转相减（除）法:

两个不同时为零的整数 \(a, b\) 的最大公约数是 \(a, b\) 线性组合（linear combination）得到的最小正整数。

由此得出欧几里得算法:

int gcd(int a, int b) { return !b ? a : gcd(b, a % b); }

大整数因为取模时间复杂度较高，用加减代替乘除可以更快的求解（python）


Stein 算法优化 :

若\(2|a, 2|b\)，\(\gcd(a,b)=2\gcd(\frac{a}{2},\frac{b}{2})\)。 否则，若\(2|a\)（\(2|b\)同理），因为\(2|b\)的情况已经讨论过了，所以\(2\nmid b\)。

因此\(\gcd(a,b)=\gcd(\frac{a}{2},b)\)。 优化后的算法（即Stein算法）

时间复杂度是\(O(\log n)\)。


Tips

1.求多个数的gcd维护差分数组

2.(\(2^a - 1\) ,\(2^b - 1\) )= \(2^{\gcd(a, b)} - 1\). （gcd同样推导）

3.多个数的gcd和lcm有结合律,



同余

同余式

定义 如果\(a\)、\(b\)除以\(m(\geq 1)\)所得的余数相同，那么称\(a\)、\(b\)对模\(m\)同余，记作\(a\equiv b(\bmod m)\). 否则，称\(a\)、\(b\)对模\(m\)不同余，记作\(a\not\equiv b(\bmod m)\).

性质1 \(a\equiv b(\bmod m)\)的充要条件是\(m|a-b\).

性质2：同余具有自反、对称、传递的性质

性质3：\(a\equiv b (mod\ m),c \equiv d (mod\ m) \Rightarrow a\pm b\equiv c\pm d ,\ ab \equiv cd\)

性质4：\(a \equiv b (mod\ m)\Rightarrow a^n \equiv b^n (mod\ m),n 为正整数\)

性质 5:若 \(a \equiv b (\text{mod } m_1)\)，\(a \equiv b (\text{mod } m_2)\)，则 \(a \equiv b (\text{mod } [m_1, m_2])\)。

对一些合并有用，否则用excrt（扩展中国剩余定理）来合并。

性质 6:若 \(ab \equiv ac (\text{mod } m)\)，则 \(b \equiv c \left(\text{mod } \frac{m}{(a, m)}\right)\)。

​ 在同余式两边约去一个数时，应将该数与 \(m\) 的最大公因数在“参照物”中同时约去。

性质 7: 如果 \((a, m) = 1\)，那么存在整数 \(b\)，使得 \(ab \equiv 1 (\text{mod } m)\)。

​ 这个 \(b\) 称为 \(a\) 对模 \(m\) 的数论倒数（逆元），贝祖定理即可证明。

有4种求逆元的算法，这里不做讲解。

点击查看代码 
//求逆元

4 EXGCD// ax+by = gcd(a,b)
	void exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) x = 1, y = 0;
    else exgcd(b, a % b, y, x), y -= a / b * x;
}
int main() {
    ll x, y;
    Exgcd (a, p, x, y);
    x = (x % p + p) % p;			//保证正数
    printf ("%d\n", x);				//x是a在mod p下的逆元

	ll a,b,c;								//求线性方程
    cin>>a>>b>>c;
    ll x,y;
    exgcd(a,b,x,y);
    if(c%g){cout<<-1;return;}
    x=x*(c/g),y=y*(c/g);
    ll dx = b/g,dy = a/g;
    ll l = ceil((double)(1-x)/dx),r = floor((double)(y-1)/dy);
    if(r<l) cout<<x+l*dx<<' '<<y-r*dy;
    else cout<<r-l+1<<' '<<x+l*dx<<' '<<y-r*dy<<' '<<x+r*dx<<' '<<y-l*dy;
}

5.费小
// p是质数，且gcd(a,p)==1
ll fpm(ll x, ll power, ll mod) {
    x %= mod;
    ll ans = 1;
    for (; power; power >>= 1, (x *= x) %= mod)
    	if(power & 1) (ans *= x) %= mod;
    return ans;
}
int main() {
	ll x = fpm(a, p - 2, p); //x为a在mod p意义下的逆元
}

6.递推法 
//inv(i) = (p-k)*i*inv(r);		p = k*i+r;
//只适用于p为质数的情况，要解模的逆元的数 , 数量很多，但是连续 
ll inv[N];			//储存逆元
void get_inv(ll N,ll p){
	inv[0]=inv[1]=1;
	for(ll i=1;i<=n;i++){
		inv[i]=1ll*(p-p/i)*inv[p%i]%p;
	}
}

7.阶乘法
//只适用于模数为质数的情况
ll fac[N], inv[N];
// 求出了fac阶乘，inv逆元
void get_inv(int n, ll p) {
    fac[0] = fac[1] = inv[0] = inv[1] = 1;
    for(int i = 2; i <= n; i++) {
        fac[i] = fac[i - 1] * i % p;
        inv[i] = (p - p / i) * inv[p % i] % p;
    }
	// 阶乘的逆元
    for(int i = 2; i <= n; i++) {
        inv[i] = inv[i - 1] * inv[i] % p;
    }
}

Tips

1.（弃9法）每个整数与它的数码和对9同余。（\(10^n \equiv 1 (mod\ 9)\)可证）

​ 这个结论可以推广到其他进制。

2.把同余式转化为等式，再用exgcd去求解。

3.\(2^{-1} \equiv (p+1)/2 \ (mod\ p)\)

4.\(S[(10d−1)x]=9d，\)\(∀x∈[1,10d].\) \(S[]\) 代表十进制数码和


奇数和偶数

内容就是小学生都知道的奇数加奇数等于偶数之类的东西，但用起来很难。

实质就是利用2的同余来给解有更多的约束。


完全平方数

性质 1 完全平方数 \(\equiv 0\) 或 \(1 (\text{mod } 4)\)，奇数的平方 \(\equiv 1 (\text{mod } 8)\)。

性质 2 相邻两个完全平方数之间没有一个正整数是完全平方数（这一性质经常用来证明某一类数不是完全平方数）。

性质 3 若两个互素的正整数之积是完全平方数，则这两个数都是完全平方数。

模其余的数亦有一些相应的性质。例如：完全平方数 \(\equiv 0\) 或 \(1 (\text{mod } 3)\)，完全平方数的末尾数字只能是 \(0, 1, 4, 5, 6, 9\) 等等。


同余方程

比较完整的总结是知乎上的

下面记录一些重要的概念（可以扩展到多元）：

多项式模\(m\)同余：两个多项式系数都对m同余时，称两个多项式模m同余。

多项式模\(m\)等价:对于所有整数，两多项式模m的值相同，则称两个多项式对m等价，记作\(f(x)\equiv g(x)\)

多项式模\(m\)的整除性: 如果存在一个整系数多项式\(h(x)\) ，使得\(f(x) \equiv g(x)h(x)\),则称\(f(x)\)关于模\(m\)能被\(g(x)\)整除，记作\(g(x) \mid f(x) (mod\ m)\)

\(n\)次剩余：设\(m>1,n>1,(a,m)=1\),如果二项同余方程 \(x^n-a\equiv 0\pmod{m}\) 有解，则称\(a\)为模\(m\)的\(n\)次剩余；如果无解，则称\(a\)为模\(m\)的\(n\)次非剩余。

分数：逆元可以用分数来表示,只要分母和模数互质分数就有意义。

有解的必要条件: 如果\(f(x)\equiv 0(mod\ m)\)有解,则\(f(x) \equiv 0 (mod\ d)\)（\(d \mid m\)）必有解。

解的个数：同余方程\(f(x)\equiv 0\pmod{m}\)的解的个数为 \(T=\frac{1}{m}\sum_{t=0}^{m-1}\sum_{x=0}^{m-1}e^{2\pi it\frac{f(x)}{m}}\)。


一些运算法则：

  • \(f(x)\equiv 0\pmod{m}\Leftrightarrow f(x)+mg(x)\equiv 0\pmod{m}\)

  • \(f(x)\equiv 0\pmod{m}\Leftrightarrow f(x)+g(x)\equiv g(x)\pmod{m}\)

  • 若\((a,m)=1\),则 \(f(x)\equiv 0\pmod{m}\Leftrightarrow af(x)\equiv 0\pmod{m}\).

  • 多项式辗转相除法：若同余方程\(h(x)\equiv 0\pmod{m}\)有\(m\)个解（即为恒等同余式），有整系数多项式\(q(x),r(x)\)满足\(f(x)\equiv q(x)h(x)+r(x)\pmod{m}\),那么 \(f(x)\equiv 0\pmod{m}\Leftrightarrow r(x)\equiv 0\pmod{m}\).

    如果\(f(x)\)的最高次项系数为1，那么满足\(f(x)=q(x)h(x)+r(x)\)的多项式\(h(x),r(x)\)一定存在，并且\(r(x)\)的次数小于\(h(x)\)的次数。

    利用该等价变形可以降低同余方程的次数。关键是找到恒等同余式\(h(x)\equiv 0\pmod{m}\).

    常用的是\(p\)为素数的恒等同余式\(x^p-x\equiv 0\pmod{p}\)


技巧

1.首项系数归一化：若\((a_n,m)=1 \land a_na_n^{-1} \equiv 1(mod\ m)\)，则可以用方程两边同时乘以\(a_n^{-1}\)的方法实现首项系数为1。

2.降次法：通过多项式辗转相除法，可以将\(f(x)\)的最高幂次缩小到小于\(m\)。

3.\((x-a)|f(x)\pmod{m}\)的充分必要条件是\(f(a)\equiv 0\pmod{m}\)


线性同余方程

形如 \(ax\equiv b(mod\ m)\)的一类方程，其中a,b,m 均为已知数， x 为未知数。

将其转化为不定方程\(ax+my = b\)用exgcd求解。


线性同余方程组

一元见扩展中国剩余定理

多元可以运用线性代数中的高斯消元法，在模意义下进行消元，再借助解一元线性同余方程组的方法完成求解


高次同余方程

由中国剩余定理可知，讨论一元不定方程\(f(x)\equiv 0\pmod{m}\)只需要讨论按\(m\)的标准分解所得到的同余方程组。即\(m=p_1^{\alpha_1}\cdots p_k^{\alpha_k}\),其中的每个素数幂两两互素，求解\(f(x)\equiv 0\pmod{p^\alpha}\)。

所以只需讨论素数幂模同余方程。

而若\(f(x)\equiv 0\pmod{m}\)有解，则对任意\(m\)的因子\(d|m,f(x)\equiv 0\pmod{d}\)也有解。

设\(x\equiv c_1,\ldots,c_t\pmod{d}\)是\(f(x)\equiv 0\pmod{d}\)的全部解，则对\(f(x)\equiv 0\pmod{m}\)的每个解\(a\),有且仅有一个\(c_i(1\leq i\leq t)\)满足\(a\equiv c_i\pmod{d}\).

这说明，可以先求出模为因子\(d\)的同余方程的全部解\(c_1,\ldots,c_t\),然后对每个\(c_i\)求\(f(x)\equiv 0\pmod{m}\)的形如\(x=c_i+dy\)的解，即解变量为\(y\)的同余方程\(g_i(y)=f(c_i+dy)\equiv 0\pmod{m}\),由此可求出原方程的全部解。

当\(m=p^\alpha\)时取\(d=p^{\alpha-1}\),这时\(g_i(y)\equiv 0\pmod{p^\alpha}\)是一次同余方程，是一定可解出的。因此最终可以降幂到求解模为素数\(p\)的一次同余方程。

如何降幂求解呢，

对于同余方程组： \(\begin{cases} f(x)\equiv 0\pmod{p^\alpha}\\ x\equiv c\pmod{p^{\alpha-1}} \end{cases}\) 其解可以表示为\(x\equiv c+p^{\alpha-1}y_j\pmod{p^\alpha}\),其中\(y_j\)是一次同余方程\(f'(c)y\equiv -f(c)p^{1-\alpha}\pmod{p}\)的全部解。 这里\(f'(x)\)表示\(f(x)\)的一阶导数，即\(f'(x)=\sum_{i=1}^{n}ia_ix^{i-1}\)。

关于解的讨论，

  1. 当\(p\nmid f'(c)\)时，方程解数为1。所以同余方程组\(\begin{cases}f(x)\equiv 0\pmod{p^\alpha}\\x\equiv c\pmod{p^{\alpha-1}}\end{cases}\)的解数为1。
  2. 当\(p|f'(c),p\nmid f(c)p^{1-\alpha}\)时，即\(f(c)\not\equiv 0\pmod{p^\alpha}\),方程无解。所以同余方程组\(\begin{cases}f(x)\equiv 0\pmod{p^\alpha}\\x\equiv c\pmod{p^{\alpha-1}}\end{cases}\)无解。
  3. 当\(p|f'(c),p|f(c)p^{1-\alpha}\)时，即\(f(c)\equiv 0\pmod{p^\alpha}\),方程的解数为\(p\),即\(y=0,1,\ldots,p-1\pmod{p}\).所以同余方程组\(\begin{cases}f(x)\equiv 0\pmod{p^\alpha}\\x\equiv c\pmod{p^{\alpha-1}}\end{cases}\)的解数为\(p\)。

数论书上是是这样将素数幂模同余方程转化为素数同余方程的：

设\(x\equiv x_1 (mod\ p)\) 是\(f(x) \equiv 0(mod\ p )\)的一个解且\(p \nmid f'(x)\) ，则\(f(x) \equiv 0(mod\ p^\alpha )\)的一解为

\[x = x_\alpha+p^\alpha t_\alpha,t_\alpha \in \Z \]

即\(x \equiv x_\alpha (mod\ p^\alpha)\),其中\(x_\alpha \equiv x_1(mod\ p)\)

但是素数模的同余方程没有固定解法，只能研究解的性质，在此不再啰嗦。

由此还有些推论：

Lagrange 定理：\(n\)次同余方程至多有n个不同的解

推论：若解数大于\(n\)，则所有系数都能被质数\(p\)整除


还有一些特殊的方程

二次剩余

当\((a,p)=1\)时,(不)存在\(x\)满足\(x^2 \equiv a (mod\ p)\) ,则称\(a\)为模\(p\)的二次(非)剩余。

\(p=2\)的情况显然。下面只讨论\(p\)为奇素数的情况。

欧拉准则:

  1. \(a\) 是 \(p\) 的二次剩余当且仅当 \(a^{\frac{p-1}{2}}\equiv 1\pmod{p}\).

  2. \(a\) 是 \(p\) 的二次非剩余当且仅当 \(a^{\frac{p-1}{2}}\equiv -1\pmod{p}\).

而且模\(p\)的二次剩余有\((p-1)/2\)个

Legendre符号:

对奇素数\(p\)和整数有

\[\left(\frac{a}{p}\right)=\begin{cases}0,& p|a,\\1,& (p\nmid a)\land((\exists x\in\mathbb{Z}),\ a\equiv x^2\pmod{p}),\\-1,& \text{otherwise.}\end{cases} \]

性质：

1.是完全积性函数

2.\(a \equiv b (mod\ p)\iff (\frac{a}{p})=(\frac {b}{p})\)

3.\(a^{\frac{p-1}{2}}\equiv \left(\frac{a}{p}\right)\pmod{p}\)

二次互反律 设\(p,q\)是两个不同的奇素数，则 \(\left(\frac{p}{q}\right)\left(\frac{q}{p}\right)=(-1)^{\frac{p-1}{2}\cdot\frac{q-1}{2}}\)

用于确定使数\(n\)为二次剩余的模数的结构。

Gauss 引理 设\((n,p)=1\),对整数\(k\left(1\leq k\leq\frac{p-1}{2}\right)\),令\(r_k\)为\(nk\)模\(p\)的最小非负剩余，设\(m\)为所有\(r_k\)中大于\(\frac{p}{2}\)的个数，则 \(\left(\frac{n}{p}\right)=(-1)^m\)

因此可以证明，对奇素数\(p\),

\(\begin{aligned}\left(\frac{2}{p}\right)&=(-1)^{\frac{p^2-1}{8}}\\&=\begin{cases}1,& p\equiv\pm1\pmod{8}\\-1,& p\equiv\pm3\pmod{8}\end{cases}\end{aligned}\)

Cipolla算法

可以用来求解二次剩余

先找到一个\(n\)使得\(n^2-a\)是二次非剩余，令\(i^2\equiv n^2-a\pmod{p}\),则\((n+i)^{\frac{p+1}{2}}\)即是方程的一个解，其相反数则是另一个解。

证明略。

点击查看代码 
struct num {
	ll x;// 实部
	ll y;// 虚部(即虚数单位√w的系数)
};

ll t,w,n,p;

num mul(num a,num b,ll p) {// 复数乘法 
	num res;
	res.x=( (a.x*b.x%p+a.y*b.y%p*w%p) %p+p)%p;// x = a.x*b.x + a.y*b.y*w
	res.y=( (a.x*b.y%p+a.y*b.x%p) %p+p)%p;// y = a.x*b.y + a.y*b.x
	return res;
}
ll qpow_r(ll a,ll b,ll p) {// 实数快速幂 
	ll res=1;
	while(b) {
		if(b&1) res=res*a%p;
		a=a*a%p;
		b>>=1;
	}
	return res;
}
ll qpow_i(num a,ll b,ll p) {// 复数快速幂  
	num res={1,0};
	while(b) {
		if(b&1) res=mul(res,a,p);
		a=mul(a,a,p);
		b>>=1;
	}
	return res.x%p;// 只用返回实数部分，因为虚数部分没了 
}
ll cipolla(ll n,ll p) {
	n%=p;
	if(qpow_r(n,(p-1)/2,p)==-1+p) return -1;// 据欧拉准则判定是否有解 
	
	ll a;
	while(1) {// 找出一个符合条件的a
		a=rand()%p;
		w=( ((a*a)%p-n) %p+p)%p;// w = a^2 - n，虚数单位的平方
		if(qpow_r(w,(p-1)/2,p)==-1+p) break;
	}
	
	num x={a,1};
	return qpow_i(x,(p+1)/2,p);
}

void solve(){ 
    int a,p;cin>>a>>p;
    if(!a){cout<<0<<endl;return;}
    ll ans1 = cipolla(a,p),ans2=-ans1+p; // 另一个解为相反数
    if(ans1==-1){cout<<"Hola!"<<endl;return;}
    if(ans1>ans2)swap(ans1,ans2);
    if(ans2==ans1)cout<<ans2<<endl;
    else cout<<ans1<<' '<<ans2<<endl;
}

k次剩余

令\(k \ge 2, (a,m) = 1\)，若有\(x\)(不)满足\(x^k \equiv a (mod\ m)\),则称\(a\)为模\(m\)的\(k\)次(非)剩余
性质：

当整数\(k\geq 2\),整数\(a,m\)满足\((a,m)=1\),模\(m\)有原根\(g\)时，令\(d=(k,\varphi(m))\),则:

  1. \(a\)为模\(m\)的\(k\)次剩余当且仅当\(d|\operatorname{ind}_ga\),即: \(a^{\frac{\varphi(m)}{d}}\equiv 1\pmod{m}\)

  2. 方程(1)若有解，则模\(m\)下恰有\(d\)个解

  3. 模\(m\)的\(k\)次剩余类的个数为\(\frac{\varphi(m)}{d}\),其有形式 \(a\equiv g^{di}\pmod{m},\quad\left(0\leq i<\frac{\varphi(m)}{d}\right)\)



不定方程

丢番图方程

除了 9n±4 型自然数外，所有 100 以内的自然数都能写成三个整数的立方和。

线性丢番图方程

线性丢番图方程（Linear Diophantine Equations）是形如 \(ax+by=c,\quad a,b,c\in\mathbb{Z}\) 的整数方程

需求出整数解\(x,y\)。

根据斐蜀定理，\(c\)是\((a,b)\)的倍数时有无数个解，令特解为\(x_0,y_0\),有通解为:

\[x=x_0+\frac{bn}{d}, y=y_0-\frac{an}{d}, n\in\mathbb{Z} \]

证明略。通解具有唯一性。特解求法使用扩展欧几里得算法

且有结论:

1.\(c>ab-a-b\)时，方程才有非负整数解

用数学归纳法可以证明\(n\)元的线性丢番图方程\(a_1x_1+\ldots+a_nx_n=c\)，当且仅当\((a_1,...,a_n) \mid c\)有且有无数个解

。通解表达很麻烦，但也是类似的思路。特解将\(n\)元拆分成n-1个2元的方程求解：

\(a_1x_1 + a_2x_2 = d_2t_2\)，$ d_2t_2 + a_3x_3 = d_3t_3 $ ，$ ... $ ，\(d_{n-1}t_{n-1} + a_nx_n = c\)（\(d_i=(a_{i-1},a_i)\)）

如何求解多元线性不定方程(组)，常见的手段有：

1.涉及非负整数解时，可以用不等式估计的方法限制未知数范围。

2.可以用数字的个数代替数字本身来求解一些方程

​ 如： 求所有的正整数数组\((a_1, a_2, \cdots, a_n)\)，使得 \(\begin{cases} a_1\leq a_2\leq\cdots\leq a_n, \\ a_1+a_2+\cdots+a_n=26, \\ a_1^2+a_2^2+\cdots+a_n^2=62, \\ a_1^3+a_2^3+\cdots+a_n^3=164. \end{cases}\)

3.求出特解来表示通解来进行下一步讨论

4.利用正整数不小于1的事实，将一些不等式转换为不定方程


高次不定方程

一般是数学竞赛里的内容，本文只摘录竞赛书上简单的介绍并附上一些例题

因式分解法

将方程的一边变为常数，而含字母的那一边可以进行因式分解，这样对常数进行素因数分解后，对比方程两边，考察各因式的每种取值情况就可将不定方程变为若干个方程组去求解。这就是因式分解法处理不定方程的基本思路。

例题：求\(xy-10(x+y)=1\)的整数解。

解 利用十字相乘，可将①变形为

\((x-10)(y-10)=101,\)

而101为素数，故

\((x-10,y-10)=(1,101),(101,1),(-1,-101),(-101,-1).\)

分别求解，得方程的整数解为

\((x,y)=(11,111),(111,11),(9,-91),(-91,9).\)

配方法

配方是代数变形中的常见方法，在处理不定方程的问题时还可综合利用完全平方数的特性，因此配方法在求解不定方程时大有用武之地。

例题：求所有的正整数\(a, b\)，使得

\[4a^{4} + 4a^{2} + 4 = b^{2} \quad \text{(1)} \]

解：
若\((a,b)\)是满足(1)的正整数对，则：

  1. \(b^{2}\)为偶数，且\(b^{2} > 4a^{4} + 4a^{2}\)
  2. 从而\(b\)为偶数，且\(b > 2a^{2} + 2\)

于是有不等式：

\[4a^{4} + 4a^{2} + 4 = b^{2} \geq (2a^{2} + 2)^{2} = 4a^{4} + 8a^{2} + 4 \]

化简可得： \(a^{2} \leq 2^{a}\)

（注：通过归纳法可证当\(a \geq 5\)时，\(a^{2} < 2^{a}\)）

分别代入\(a = 1,2,3,4\)测试：

  • \(a=1\)：无解
  • \(a=2\)：\(b=6\)
  • \(a=3\)：无解
  • \(a=4\)：\(b=18\)

结论：方程的所有正整数解为
\((a,b)=(2,6)\) 或 \((4,18)\)

不等式估计

利用不等式的知识，先确定不定方程中的某个字母的范围，然后逐个枚举得到所有解，这个方法称为不等式估计，它也是我们处理不定方程的常见方法。当然，如果能够恰当地利用字母的对称性等，那么作不等式估计时会简洁很多。

例题略，从其他的例题也能看出不等式估计的重要性。

同余方法

若不定方程\(F(x_1,x_2,\cdots,x_n)=0\)有整数解，则对任意的\(m\in\mathbb{N}^*\)，其整数解\((x_1,x_2,\cdots,x_n)\)都满足

\(F(x_1,x_2,\cdots,x_n)\equiv 0(\bmod m).\)

运用这个必要条件，同余可以作为不定方程是否有整数解的一块试金石。

例题：证明：不定方程 \(x^2+y^2-8z^3=6\) 没有整数解。

若\((x,y,z)\)是方程①的整数解，对①的两边模2，可知\(x\)、\(y\)同奇偶；再对①两边模4可知\(x\)、\(y\)都为奇数。

于是\(x^2\equiv y^2\equiv 1(\bmod 8)\)，这要求 \(6=x^2+y^2-8z^3\equiv 2(\bmod 8),\) 矛盾。故方程①没有整数解。

这说明利用同余方法解不定方程问题时，选择恰当的数作为模是十分重要的，它不仅涉及问题解决的繁简程度，重要的是能否卡住字母的范围或导出矛盾。

构造法

有些不定方程的问题只讨论该方程是否有解或有无穷多个解，这时经常会采用构造法来处理。

例题：证明：方程 ($ x^2 + y^5 = z^3 $) 有无穷多组满足 ( $xyz \neq 0 $) 的整数解。

取 ( \(x = 2^{15k+10}\) )，($ y = 2^{6k+4} $)，( $z = 2^{10k+7} $)，其中 ( k ) 为非负整数。

则这样的 ( (x, y, z) ) 满足 ( \(x^2 + y^5 = z^3\) )，且 ( \(xyz \neq 0\) )。由于 ( k ) 可以取无穷多个非负整数值，因此原方程有无穷多组满足条件的整数解。


勾股方程

求解不定方程\(x^2 + y^2 = z^2\) ①

注意到，对①的解\((x,y,z)\)，如果\((x,y)=d\)，那么\(d^2|z^2\)，即有\(d|z\)，因此可以在①的两边约去\(d\)后再讨论。

这说明我们只需在条件\((x,y)=1\)下，求①的所有正整数解。

易知当\((x,y)=1\)时，\(x\)、\(y\)、\(z\)两两互素，我们称①的使得\(x\)、\(y\)、\(z\)两两互素的正整数解\((x,y,z)\)为本原勾股数组Primitive Pythagorean Triple (PPT)。

下面来求①的所有本原勾股数组。

设\((x,y,z)\)是①的一个本原解（即\((x,y,z)\)是本原勾股数组），则由\((x,y)=1\)，知\(x\)、\(y\)不同为偶数；

若\(x\)、\(y\)都是奇数，则

\[z^2=x^2+y^2\equiv 1+1=2(\bmod 4) \]

这与完全平方数\(\equiv 0\)或\(1(\bmod 4)\)矛盾，所以\(x\)、\(y\)不同为奇数，即\(x\)、\(y\)是一奇一偶。 不妨设\(y\)为偶数，则\(x\)、\(z\)都是奇数，由①得 \(y^2=z^2-x^2,\) 故 \(\left(\frac{y}{2}\right)^2=\frac{z-x}{2}*\frac{z+x}{2}.\)

而由

\(\begin{aligned} \left(\frac{z-x}{2},\frac{z+x}{2}\right)&=\left(\frac{z-x}{2},\frac{z+x}{2}+\frac{z-x}{2}\right)\\ &=\left(\frac{z-x}{2},z\right)=(z-x,z)\\ &=(x,z)=1, \end{aligned}\)

可知\(\frac{z-x}{2}\)与\(\frac{z+x}{2}\)都是完全平方数，所以，可设 \(\left(\frac{z-x}{2},\frac{z+x}{2}\right)=(m^2,n^2),\) 依此得 \(y=2mn.\)

进一步，由\(\left(\frac{z-x}{2},\frac{z+x}{2}\right)=1\)，可知\((m,n)=1\)，而由\(x\)、\(z\)都是奇数，知\(m\)、\(n\)一奇一偶。

综上可知，①的所有本原解为 \(\begin{cases} x=n^2-m^2\\ y=2mn\\ z=m^2+n^2 \end{cases}\)或 \(\begin{cases} x=2mn\\ y=n^2-m^2\\ z=m^2+n^2\end{cases}\)

其中\(m\)、\(n\)为正整数，\(m<n\)，且\((m,n)=1\)，\(m\)、\(n\)一奇一偶。

再乘以一个d就能得到所有解。

关键点：

1.\((x,y)=d\Rightarrow (x,y)=1\)，直接讨论本原解

2.x和y只能是一奇一偶的讨论

3.对完全平方数的讨论

但一般数论问题不会用到解的形式，关键是勾股方程有无穷多组（本原的）正整数解。

费马还对此进行了\(x^n+y^n=z^n\)的研究，发现\(n>3\)时无正整数解。



欧拉函数

欧拉函数 \(\varphi(N)\) 定义为 \(1\) 到 \(N\) 中与 \(N\) 互质的数的个数（其中 \(p_1, p_2, \ldots\) 是 \(N\) 的质因子）： $$ \varphi(N) = N \prod_{i} \left(1 - \frac{1}{p_i}\right) $$

性质：

  1. 与 \(N\) 互质的数的和是 \(\frac{N \cdot \varphi(N)}{2}\)。
  2. 对于质数 \(p\)，有 \(\varphi(p) = p - 1\)。
  3. 若 \(a\) 和 \(b\) 互质，则 $$ \varphi(a \cdot b) = \varphi(a) \cdot \varphi(b) $$

​ 若\((a,b)=d\),则\(\varphi(ab)=\frac{\varphi(a)\varphi(b)}{\prod_{p|d}\left(1-\frac{1}{p}\right)}=\frac{d}{\varphi(d)}\varphi(a)\varphi(b)\)。

5.当 \(p\) 为质数且 \(p|n\)，\(p^2|n\) 时， $$ \varphi(n) = \varphi(n/p) \cdot p $$

6.当 \(p\) 为质数且 \(p|n\) 但 \(p^2\) 不整除 \(n\) 时， $$ \varphi(n) = \varphi(n/p) \cdot (p-1) $$

7.\(\sum_{d|m}\varphi(d)=m\)

这里注意完全平方数的根不要重复算贡献

8.\(when\ n>2\)，\(\varphi(n)>2 \land \varphi(n)\ is\ even\)

9.若 \(a,n\) 互质，则满足 $a^x≡1(mod\ n) $的最小正整数解为 \(φ(n)\) 的约数。


欧拉反演

常常用于化简一列最大公约数的和。

欧拉函数常常用于化简一列最大公约数的和。国内有些文章称它为 欧拉反演。 在结论 \(n=\sum_{d|n}\varphi(d)\) 中代入\(n=\gcd(a,b)\),则有 \(\gcd(a,b)=\sum_{d|\gcd(a,b)}\varphi(d)=\sum_{d}[d|a][d|b]\varphi(d)\)

\(\sum_{i=1}^{n}\gcd(i,n)=\sum_{d}\sum_{i=1}^{n}[d|i][d|n]\varphi(d)=\sum_{d}\left\lfloor\frac{n}{d}\right\rfloor[d|n]\varphi(d)=\sum_{d|n}\left\lfloor\frac{n}{d}\right\rfloor\varphi(d).\)

这里关键的观察是\(\sum_{i=1}^{n}[d|i]=\left\lfloor\frac{n}{d}\right\rfloor\),即在1和\(n\)之间能够被\(d\)整除的\(i\)的个数是\(\left\lfloor\frac{n}{d}\right\rfloor\)。

其中,\([\cdot]\)称为Iverson括号,只有当命题\(P\)为真时\([P]\)取值为1,否则取0。

例题

点击查看代码 
#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using ll = long long;
using i128 = __int128;
using namespace std;

vector<int> primes,phi;
vector<bool> nop;
void euler(int n) {
    phi.assign(n + 1, 0);
    nop.assign(n + 1, 0);
    // primes.clear();
    phi[1]=1;
    for (int i = 2; i <= n; i++) {
        if (nop[i]==0) {
            primes.push_back(i);
            phi[i]=i-1;
        }
        
        for (auto p : primes) {
            if (i * p > n)break;
            nop[i*p]=1;
            if (i%p==0) {
                phi[i*p]=phi[i]*p;
                break;
            }
            phi[i*p]=phi[i]*phi[p];
        }
    }
}

void solve(){
    int n;cin>>n;
    int ans = 0;
    euler(n);
    for(int i=1;i<=n;i++){
        ans+=phi[i]*(n/i)*(n/i);
    }
    cout<<ans;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int tt =1;
    // cin>>tt;
    while (tt--)solve();
    return 0;
}




定理

裴蜀定理 (Bezout 定理)

结论 设 \(d = (a, b)\)，则存在整数 \(x, y\)，使得

\[ax + by = d \]

推论 若 $ a, b $ 互素，则有整数 $ m, n $ 满足 $ ma + nb = 1 $

证明：

不妨设 \(a, b\) 都不为零（当 \(a, b\) 中有一个为零时，结论是显然的），且 \(|a| \leq |b|\)。

设 \(b = aq_1 + r_1\)，其中 \(0 \leq r_1 < |a|\)，\(q_1, r_1\) 为整数。若 \(r_1 = 0\)，则辗转相除到此为止；否则用 \(a\) 去除以 \(r_1\)，得等式 \(a = r_1 q_2 + r_2\)，\(0 \leq r_2 < r_1\)；依此讨论，由于 \(r_1 > r_2 > r_3 > \cdots\)，因此辗转相除到某一步后，所得的 \(r_{k+1} = 0\)，于是，我们得到了如下的一系列式子：

\[\begin{aligned} b &= aq_1 + r_1, \quad 0 < r_1 < |a|; \\ a &= r_1 q_2 + r_2, \quad 0 < r_2 < r_1; \\ r_1 &= r_2 q_3 + r_3, \quad 0 < r_3 < r_2; \\ &\vdots \\ r_{k-2} &= r_{k-1} q_k + r_k, \quad 0 < r_k < r_{k-1}; \\ r_{k-1} &= r_k q_{k+1}. \end{aligned} \]

注意到，从第一个式子到第 \(k\) 个式子，我们依次有

\[ d \mid r_1, \quad d \mid r_2, \quad \cdots, \quad d \mid r_k, \]

而从第 \(k+1\) 个式子倒推，又依次有

\[ r_k \mid r_{k-1}, \quad r_k \mid r_{k-2}, \quad \cdots, \quad r_k \mid r_1, \quad r_k \mid a, \quad r_k \mid b, \]

所以，\(r_k\) 也是 \(a, b\) 的公因数，结合 \(d\) 为 \(a, b\) 的最大公因数知 \(r_k \leq d\)，又 \(d \mid r_k\)，故 \(d \leq r_k\)，因此，\(d = r_k\)，也就是说，我们求出了 \(a, b\) 的最大公因数。

现在，利用 \(d = r_k\) 及第 \(k\) 个式子，可知

\[ d = r_{k-2} - r_{k-1} q_k. \]

再由 \(r_{k-1} = r_{k-3} - r_{k-2} q_{k-1}\)（第 \(k-1\) 个式子变形得），代入上式，可知 \(d\) 可以表示为 \(r_{k-2}\) 与 \(r_{k-3}\) 的“线性组合”，依此倒推，可知 \(d\) 可以表示为 \(a, b\) 的“线性组合”，即存在整数 \(x, y\) 使得

\[ d = ax + by. \]

说明 反过来，设 \(x, y\) 为整数，\(d' = ax + by\)，并不能推出 \(d'\) 为 \(a, b\) 的最大公因数。事实上，可以证明：\(a, b\) 的最大公因数是形如 \(ax + by\)（\(x, y\) 为任意整数）的正整数中最小的那个。


扩展裴蜀定理:
对互素的自然数 $a 、 b $和整数 \(n\) ， 考察不定方程：$ ax+by=n \( 其中\) x,y$为自然数。如果方程有解，称 \(n\)可以被\(x,y\)表示。
记 \(C=ab-a-b\)。由 \(a\) 与 \(b\) 互素， \(C\) 必然为奇数。则有结论：
对任意的整数 \(n\) ， \(n\) 与 \(C-n\) 中有且仅有一个可以被表示。
即：可表示的数与不可表示的数在区间 \(0,C\)对称（关于\(C\)的一半对称）。 \(0\)可被表示， \(C\) 不可被表示；负数不可被表示，大于 \(C\)的数可被表示。


威尔逊定理

\((p-1)!\equiv -1 (mod\ p) \iff p\)为质数

拓展：

对于自然数\(m>1\),有 \(\prod_{\substack{1\leq k<m,k\perp m}}k\equiv \pm 1\pmod{m}.\)

而且，余数中的\(\pm 1\)取值为\(-1\)当且仅当模\(m\)的原根存在，即\(m=2,4,p^\alpha,2p^\alpha\)时，其中\(p\)是奇素数且\(\alpha\)是正整数。

对于素数\(p\)和正整数\(\alpha\),有 \(\prod_{\substack{1\leq k<p^\alpha,\ k\perp p}}k\equiv \begin{cases} 1,&p=2\text{ and }\alpha\geq 3,\\ -1,&\text{otherwise} \end{cases}\pmod{p^\alpha}.\)


欧拉定理

对 \(a \in \mathbb{Z}\)，\(m \in \mathbb{N}^*\)，若 \((a, m) = 1\)，则 $ a^{\varphi(m)} \equiv 1 \pmod{m}. $

欧拉定理推论
\(a^b \equiv \begin{cases} a^{b \mod \varphi(m)} & \gcd(a, m) = 1 \\ a^b & \gcd(a, m) \neq 1, b < \varphi(m), \\ a^{(b \mod \varphi(m)) + \varphi(m)} & gcd(a,m) \neq 1,\ b \geq \varphi(m). \end{cases} \pmod{m}\)

有时第二，三条也称为欧拉降幂公式。

注意第二，三条的限制，否则会出错(如$2^1 mod\ 4 = 2\ $用强行用欧拉降幂公式会得到0)

点击查看代码 
#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using ll = long long;
using i128 = __int128;
using namespace std;


i128 qpow(i128 a,i128 b,i128 mod){
	i128 res = 1;
	while(b){
		if(b&1) res = res*a %mod;
		a = a*a %mod;
		b >>= 1;
	}
	return (res%mod+mod)%mod;
}

int p=1e9+7;
bool fl=0;
inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();if(x>p)x%=p,fl=1;}
	return x*f;
}

int phi(int n) {
    int res = n;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            while (n % i == 0)  n /= i;
            res = res / i * (i - 1);
        }
    }
    if (n > 1) res = res / n * (n - 1);
    return res;
}

void solve(){
	int a,m,b;
	a=read(),m=read();
	a%=m;
	p=phi(m);
	b=read();
	if(fl)b+=p;
	int ans =qpow(a,b,m);
	printf("%d",ans);
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int tt =1;
    // cin>>tt;
    while (tt--)solve();
    return 0;
}

费马小定理

若 $ p $ 为素数，\(\gcd(a, p) = 1\)，则 $ a^{p-1} \equiv 1 \pmod{p}. $

另一个形式：若p为素数，对于任意整数 $ a $，有 $ a^p \equiv a \pmod{p}. $

第二个形式在多项式展转相除法中很重要，其证明用到了二项式展开。


中国剩余定理

线性同余方程组

\(\left\{ \begin{array}{ll} x & \equiv a_1 \pmod{n_1} \\ x & \equiv a_2 \pmod{n_2} \\ & \vdots \\ x & \equiv a_k \pmod{n_k} \end{array} \right.\) (其中\(n_1,n_2...n_k\)两两互质)

的通解为\(ans=i∑r_i⋅M_i⋅inv(M_i,m_i)\)


拉格朗日定理

设 $ p $ 为素数，对于模 $ p $ 意义下的整系数多项式 $$ f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_0 \quad (p \nmid a_n) $$ 的同余方程 $ f(x) \equiv 0 \ (\text{mod}\ p) $ 在模 $ p $ 意义下至多有 $ n $ 个不同解。


升幂引理

升幂（Lift the Exponent，LTE）引理:用来求解用于求解多项式方程和同余方程的高次幂解

我们用\(\nu_p(n)\)表示\(n\)的标准分解中素数\(p\)的幂次，也即若\(p^k\mid n \land p^{k+1}\nmid n\),则\(\nu_p(n)=k\)。

常用的部分：

1.\(p\)为奇素数时：

\(p\mid a-b,(p,ab)=1\),则\(\nu_p(a^n-b^n)=\nu_p(a-b)+\nu_p(n)\), \(\nu_p(a^n+b^n)=\nu_p(a+b)+\nu_p(n)\)。

2.\(p=2\)，且\((2,ab)=1\)时：

若\(4 \mid a-b\),\(\nu_2(a^n-b^n)=\nu_2(a-b)+\nu_2(n)\)

若\(n\)为奇数,\(\nu_2(a^n-b^n)=\nu_2(a-b)\)

若\(n\)为偶数,则有$ v_2(a^n - b^n) = v_2(a - b) + v_2(a + b) + v_2(n) - 1 $


卢卡斯定理

虽然已经很熟了，这里还是规定一下：组合数可以表示为\(\binom{n}{k}=\frac{n!}{k!(n-k)!}.\)

对于素数\(p\),有 \(\binom{n}{k}\equiv\binom{\lfloor n/p\rfloor}{\lfloor k/p\rfloor}\binom{n\bmod p}{k\bmod p}\pmod{p}.\) 其中，当\(n<k\)时，二项式系数\(\binom{n}{k}\)规定为0。

ll lucas(ll n,ll m,ll p){
	if(!m)return 1;
	return 1ll*lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

推论：

  • 当且仅当存在\(i\in\{0,1,2,\ldots,k\}\)使得\(n_i>m_i\)(p进制)时,\(C_n^m\equiv 0\pmod{p}\)

  • \(C_a^b\)为奇数的充要条件为二进制表示下\(a\)的每一位上的数都不小于\(b\)相应位上的数.

但这里要求是素数p，如果不是素数，可以用扩展卢卡斯定理


exLucas

素数幂有\(\binom{n}{k}=p^{\nu_p(n!)-\nu_p(k!)-\nu_p((n-k)!)}\frac{(n!)_p}{(k!)_p((n-k)!)_p}.\)

一般模数拆成几个素数幂的同余方程再用CRT合并即可。

点击查看代码 
//from jiangly(洛谷上超的板子)
#include <iostream>
#include <vector>
std::vector<std::pair<int, int>> factorize(int n) {
    std::vector<std::pair<int, int>> factors;
    for (int i = 2; static_cast<long long>(i) * i <= n; ++i) {
        if (n % i == 0) {
            int t = 0;
            for (; n % i == 0; n /= i)
                ++t;
            factors.emplace_back(i, t);
        }
    }
    if (n > 1)
        factors.emplace_back(n, 1);
    return factors;
}
constexpr int power(int base, long long exp) {
    int res = 1;
    for (; exp > 0; base *= base, exp /= 2)
        if (exp % 2 == 1)
            res *= base;
    return res;
}
constexpr int power(int base, long long exp, int mod) {
    int res = 1 % mod;
    for (; exp > 0; base = static_cast<long long>(base) * base % mod, exp /= 2)
        if (exp % 2 == 1)
            res = static_cast<long long>(res) * base % mod;
    return res;
}
int inverse(int a, int m) {
    int g = m, r = a, x = 0, y = 1;
    while (r != 0) {
        int q = g / r;
        g %= r;
        std::swap(g, r);
        x -= q * y;
        std::swap(x, y);
    }
    return x < 0 ? x + m : x;
}
int solveModuloEquations(const std::vector<std::pair<int, int>> &e) {
    int m = 1;
    for (std::size_t i = 0; i < e.size(); ++i)
        m *= e[i].first;
    int res = 0;
    for (std::size_t i = 0; i < e.size(); ++i) {
        int p = e[i].first;
        res = (res + static_cast<long long>(e[i].second) * (m / p) * inverse(m / p, p)) % m;
    }
    return res;
}
class Binomial {
    const int mod;
private:
    const std::vector<std::pair<int, int>> factors;
    std::vector<int> pk;
    std::vector<std::vector<int>> prod;
    static constexpr long long exponent(long long n, int p) {
        long long res = 0;
        for (n /= p; n > 0; n /= p)
            res += n;
        return res;
    }
    int product(long long n, std::size_t i) {
        int res = 1;
        int p = factors[i].first;
        for (; n > 0; n /= p)
            res = static_cast<long long>(res) * power(prod[i].back(), n / pk[i], pk[i]) % pk[i] * prod[i][n % pk[i]] % pk[i];
        return res;
    }
public:
    Binomial(int mod) : mod(mod), factors(factorize(mod)) {
        pk.resize(factors.size());
        prod.resize(factors.size());
        for (std::size_t i = 0; i < factors.size(); ++i) {
            int p = factors[i].first;
            int k = factors[i].second;
            pk[i] = power(p, k);
            prod[i].resize(pk[i]);
            prod[i][0] = 1;
            for (int j = 1; j < pk[i]; ++j) {
                if (j % p == 0) {
                    prod[i][j] = prod[i][j - 1];
                } else {
                    prod[i][j] = static_cast<long long>(prod[i][j - 1]) * j % pk[i];
                }
            }
        }
    }
    int operator()(long long n, long long m) {
        if (n < m)
            return 0;
        std::vector<std::pair<int, int>> ans(factors.size());
        for (std::size_t i = 0; i < factors.size(); ++i) {
            int p = factors[i].first;
            int k = factors[i].second;
            int e = exponent(n, p) - exponent(m, p) - exponent(n - m, p);
            if (e >= k) {
                ans[i] = std::make_pair(pk[i], 0);
            } else {
                int pn = product(n, i);
                int pm = product(m, i);
                int pd = product(n - m, i);
                int res = static_cast<long long>(pn) * inverse(pm, pk[i]) % pk[i] * inverse(pd, pk[i]) % pk[i] * power(p, e) % pk[i];
                ans[i] = std::make_pair(pk[i], res);
            }
        }
        return solveModuloEquations(ans);
    }
};
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    long long n, m;
    int p;
    std::cin >> n >> m >> p;
    Binomial binom(p);
    std::cout << binom(n, m) << "\n";
    return 0;
}


算法

扩展欧几里得算法

欧几里得算法（即辗转相除法）用来求gcd，而扩展欧几里得算法通过同样思路求出2元丢番图方程\(ax+by=(a,b)\)的通解

void exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) x = 1, y = 0;
    else exgcd(b, a % b, y, x), y -= a / b * x;
}

其实就是用\(a,b\)求\((a,b)\)再逆向将\(x,y\)推回去


万能欧几里得算法

用来解决求\(y=\left\lfloor\frac{ax+b}{c}\right\rfloor(x \in [1,n])\)这个函数的变形,如\(\sum f(x)a^xg(y)b^y,\sum y^2,\sum xy\)。

按照传统方法(类欧几里得)求\(\sum y\)就是推柿子求解：

\(f(a,b,c,n)=\frac{n(n+1)}{2}\left\lfloor\frac{a}{c}\right\rfloor+(n+1)\left\lfloor\frac{b}{c}\right\rfloor+f(a\bmod c,b\bmod c,c,n)\)

当\(a<c,b<c\),\(f(a,b,c,n)=nm-f(c,c-b-1,a,m-1)\)

（证明中出现了一个特别天才的构造，为什么不详细介绍~因为博主不会（划掉），因为不具有泛用性）

但用万能欧几里得就能得到此类问题（差分影响线性）的通解（而且好写）:

（除了如\(\sum\sqrt{y},\sum x^y,\sum a^{xy},\sum 2^{2^n},\sum A\sin(wy+\phi)\),这些问题无法设计出一个好的矩阵来表示。）


在线段\(y=\left\lfloor\frac{ax+b}{c}\right\rfloor(x \in [1,n])\)定义域内，从左到右，维护一个只含有的\(U,R\)字符串。

y与一条水平线相交就push U，与竖直线相交就push R，与整点相交就先push U再push R。

给定一个字符串函数\(f\)，求\(f(S)\)。

其中\(f\)满足运算 \(*\) :\(f(S_1)* f(S_2)=f(S_1+S_2)\)且 \(*\) 有结合律。

这样就能把一个大的字符串拆分求解

观察到解只与\(a,b,c,n,f(\texttt{U}),f(\texttt{R})\)有关，不妨将其记为\(g(a,b,c,n,f_U,f_R)\)。

1.图像按y轴平移单位长度不影响\(S\)。那么我们令\(b= b\bmod c\)。

2.当\(a\geq c\)时，直线\(y=\frac{ax+b}{c}\)相比于\(y=\frac{(a\bmod c)x+b}{c}\)，每个R前恰好会多出\(\left\lfloor\frac{a}{c}\right\rfloor\)个U。

所以我们有\(g(a,b,c,n,f_U,f_R)=g(a\bmod c,b,c,n,f_U,f_U^{\left\lfloor\frac{a}{c}\right\rfloor}\cdot f_R)\)。

3.按上面处理后\(g(a,b,c,n,f_U,f_R)\)=\(f_R^{\left\lfloor\frac{c-b-1}{a}\right\rfloor}\cdot f_U\cdot g(c,c-b-1,a,m-1,f_R,f_U)\cdot f_R^{n-\left\lfloor\frac{cm-b-1}{a}\right\rfloor}\)


下证：

（感性的证明就是把坐标轴对换，使得直线斜率大于1，继续取模，从而和欧几里得算法复杂度分析类似）

通过1,2有\(a<c，b<c\)，第\(p\)个R之前应该共有\(\left\lfloor\frac{ap+b}{c}\right\rfloor\)个U。

假设第\(p\)个R在第\(q\)个U之前。

\(q>\left\lfloor\frac{ap+b}{c}\right\rfloor\) \(q>\frac{ap+b}{c}\) \(p<\frac{cq-b}{a}\) \(p\leq\left\lfloor\frac{cq-b-1}{a}\right\rfloor\)

于是得到结论，第\(q\)个U前有\(\left\lfloor\frac{cq-b-1}{a}\right\rfloor\)个R。

所以有，答案等于\(y=\lfloor\frac{cx-b-1}{a} \rfloor ,y\in[1,n]\)，且U与R互换时的结果，设\(m=\left\lfloor\frac{an+b}{c}\right\rfloor\).

我们将答案分为三部分计算:

  • \(x\leq 1\)，这部分的结果为\(f_R^{\left\lfloor\frac{c-b-1}{a}\right\rfloor}\cdot f_U\)。

  • \(x>m\)，这部分的结果为\(f_R^{n-\left\lfloor\frac{cm-b-1}{a}\right\rfloor}\)。

  • \(1<x\leq m\)，这部分的结果即为\(g(c,c-b-1,a,m-1,f_R,f_U)\)。

总结果即为\(f_R^{\left\lfloor\frac{c-b-1}{a}\right\rfloor}\cdot f_U\cdot g(c,c-b-1,a,m-1,f_R,f_U)\cdot f_R^{n-\left\lfloor\frac{cm-b-1}{a}\right\rfloor}\)。

递归下去即可，递归边界为若\(m=0\)，则答案为\(f_R^n\)。

时间复杂度为\(O(k\log\max(a,c))\),k为$* $的时间复杂度

关键在于如何构建node三元组（参考 https://www.cnblogs.com/AThousandMoons/p/13129093.html）

举些板栗：

1.\((u,r,ans_{i,j})\)，其中\(ans_{i,j}=\sum x^i*y^j\)

​ \(A*B\)有\(ans_{a,b}=A.ans_{a,b}+ \sum^i \sum^j C_a^i C_b^j A_u^iA_j\ B.ans_{a-i,b-j}\\\)其余两项略

\(A\)部分计算不变为\(A.ans_{a,b}\)，\(B\)部分变为\(\sum (y+u)^a (x+r)^b\)

展开可以得到\(\sum^i \sum^j C_a^i C_b^j A_u^iA_j\ B.ans_{a-i,b-j}\\\)(类似于积分的把求和符号放到\(x,y\)上可得到\(B.ans_{a-i,b-j}\))

2.\((X,Y,ans)\)表示\(A^{cnt1},B^{cnt2},\sum A^xB^y\)其中（\(A,B\)为矩阵）

\((X,Y,ans)\times(X',Y',ans')\) \(=(X*X',Y*Y',ans+X*ans'*Y)\)易证

两个例子合起来就能做\(\sum f(x)A^xg(y)B^y\)了

板题

点击查看代码 
#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using ll = long long;
using i128 = __int128;
using namespace std;

const int mod =998244353,inv2=(mod+1)/2;
struct node{
	int u,r,f,g,h;
	node():u(),r(),f(),g(),h(){}
};
node operator *(node const &a,node const &b){
	node c;
	c.u=(a.u+b.u)%mod;
	c.r=(a.r+b.r)%mod;
	c.f=(a.f+b.f+1ll*b.r*a.u)%mod;
	c.g=(a.g+b.g+1ll*a.u*a.u%mod*b.r+2ll*a.u*b.f)%mod;
	c.h=(a.h+b.h+1ll*b.f*a.r+1ll*a.u*(2ll*a.r+b.r+1)%mod*b.r%mod*inv2)%mod;
	return c;
}
node pow(node a, ll b) {
    node ans;
    while (b) {
        if (b & 1) ans = ans * a;
        a = a * a;
        b >>= 1;
    }
    return ans;
}
node euclid(ll a, ll b, ll c, ll n, node U, node R) {
    if (!n) return node();
    if (b>=c) b%=c;
    if (a>=c) return euclid(a%c,b,c,n,U,pow(U,a/c)*R);
    ll m = ((i128)a*n+b)/c;
    if(!m)return pow(R, n);
    return pow(R,(c-b-1)/a)*U*euclid(c,c-b-1,a,m-1,R,U)*pow(R,n-(c*m-b-1)/a);
}

void solve(){
    ll n,a,b,c;
    cin>>n>>a>>b>>c;
    node u,r;u.u=1,r.r=1;
    node p = pow(u,b/c)*euclid(a,b,c,n,u,r);
    cout<<(p.f+b/c)%mod<<' '<<(p.g+1ll*(b/c)*(b/c))%mod<<' '<<p.h<<'\n';
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int tt =1;
    cin>>tt;
    while (tt--)solve();
    return 0;
}

扩展中国剩余定理

对于更一般的线性同余方程组，我们通过两两化为不定方程来一次求解

i128 gcd(i128 a, i128 b){return b ? gcd(b,a%b) : a;}

i128 exgcd(i128 a, i128 b, i128 &x, i128 &y) {
    if (!b) {x = 1, y = 0;return a;}
    else {i128 d=exgcd(b, a % b, y, x); y -= a / b * x;return d;}
}

ll excrt(int n,vector<ll> a,vector<ll> b){
    i128 x,y,M=b[1],ans=a[1];
    for(int i=2;i<=n;i++){
        i128 A=M,B=b[i];
        i128 C=(a[i]-ans%B+B)%B;
        i128 g=exgcd(A,B,x,y);
        if(C%g)return -1;
        x=x*(C/g)%B;
        ans+=x*M;
        M=M/gcd(M,B)*B;
        ans=(ans%M+M)%M;
    }
    return ans;
}

Garner算法

给出的模数不是质数且该模数是由一些不重复的质数相乘得到的。

那么我们可以分别对这些模数进行计算，最后用 CRT 合并答案。

例如，若\(a\)满足如下线性方程组，且\(a<\prod_{i=1}^{k}p_i\)（其中\(p_i\)为质数）：

\(\begin{cases} a&\equiv a_1(\bmod p_1)\\ a&\equiv a_2(\bmod p_2)\\ &\vdots\\ a&\equiv a_k(\bmod p_k) \end{cases}\)

我们可以用以下形式的式子（称作\(a\)的混合基数表示）表示\(a\)：

\(a=x_1+x_2p_1+x_3p_1p_2+\ldots+x_kp_1\cdots p_{k-1}\)

可以用Garner 算法计算系数\(x_1,\ldots,x_k\)。原理如下：

令\(r_{ij}\)为\(p_i\)在模\(p_j\)意义下的逆元, 得到\(p_i\cdot r_{i,j}\equiv 1\pmod{p_j}\)

把\(a\)代入我们得到的第一个方程： \(a_1\equiv x_1\pmod{p_1}\)

代入第二个方程得出： \(a_2\equiv x_1+x_2p_1\pmod{p_2}\)

方程两边减\(x_1\)，除\(p_1\)后得

\[\begin{aligned} a_2-x_1&\equiv x_2p_1\pmod{p_2}\\ (a_2-x_1)r_{1,2}&\equiv x_2\pmod{p_2}\\ x_2&\equiv (a_2-x_1)r_{1,2}\pmod{p_2} \end{aligned} \]

类似地，我们可以得到： \(x_k=\left(\ldots\left(\left(a_k-x_1\right)r_{1,k}-x_2\right)r_{2,k}\right)-\ldots)r_{k-1,k}\bmod p_k\)

//a[]储存同余数，p[]储存模数，x[]存储混合基数表示的系数
//r[i][j]储存逆元
for (int i = 0; i < k; ++i) {
  x[i] = a[i];
  for (int j = 0; j < i; ++j) {
    x[i] = r[j][i] * (x[i] - x[j]);
    x[i] = x[i] % p[i];
    if (x[i] < 0) x[i] += p[i];
  }
}

Miller-Rabin算法

费马素数测试:（1）如果\(an−1≡1(mod\ n)\)不成立，那么n不是素数。
  （2）如果\(an−1≡1(mod\ n)\)成立，那么n很大概率是素数，尝试的a越多，n是素数的概率越大。称n是一个基于a的伪素数。

伪素数中的非素数称为Carmichael数,前1e9个数中只有255个。

根据二次探测定理改进后我们得到了Miller-Rabin算法，如下

// 快速乘
ll qmul(ll a, ll b, ll m) {
    return static_cast<__int128>(a) * b % m;
}

// 快速幂：计算 (a^b) % m，使用快速乘进行模幂运算
ll qpow(ll a, ll b, ll m) {
    ll res = 1 % m;          
    for (; b; b >>= 1) {     
        if (b & 1)           
            res = qmul(res, a, m);
        a = qmul(a, a, m);  
    }
    return res;
}

// Miller-Rabin素数检测，确定n是否为素数
bool isprime(ll n) {
    if (n < 2)
        return false;
    static constexpr int A[] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
    int s = __builtin_ctzll(n - 1);  
    ll d = (n - 1) >> s;             

    for (auto a : A) {                
        if (a == n)    return true;
        ll x = qpow(a, d, n);       // 计算a^d mod n
        if (x == 1 || x == n - 1)   continue;		//通过
        bool ok = false;
        for (int i = 0; i < s - 1; ++i) {
            x = qmul(x, x, n);        
            if (x == n - 1) {       // 若得到n-1，则通过本轮
                ok = true;
                break;
            }
        }
        if (!ok)                     // 所有次平方后仍未通过，n为合数
            return false;
    }
    return true;                    // 所有基数测试通过，n为素数
}

Pollard_rho算法

可以用\(O(\sqrt p)\)次计算找到n的一个小因子\(p\)。

假设要找\(n\)的因子，根据若\(n\)为一个合数，则\(n\)有一个不大于\(\sqrt{n}\)的质因数的定理，设该质数为\(p\)。

假设存在\(x<y(1\leq x<y < n)\)，满足 \(x\equiv y(\bmod p)\Leftrightarrow p\mid (y-x)\)

因为\(p\mid n\)，\(-n<y-x<n\)且\(x_i\neq x_j\)，那么我们必须有 \(p\mid(y-x,n)\)

那么\((y-x,n)\)就是\(n\)的非平凡因子

先忽略\(p\)如何找到，如果是暴力找到 \(x\equiv y(\bmod p)\) 的期望相当于\(O(\frac {\sqrt n} {2} )\) ，糖丸了。

肯定需要优化:

使用伪随机数序列，构造一个函数\(f\)使得\(f(y) \equiv f(x) (mod\ p) \iff y \equiv x (mod\ p)\)

一般在\(mod\ n\)的情况下用\(f(k+1) = k^2+1\)

根据生日悖论，对于一个随机自映射\(f:\mathbb{Z}_p\to\mathbb{Z}_p\)，从任何一点\(x_1\)出发，迭代计算\(x_n=f(x_{n-1})\)，将在\(O(\sqrt{p})\)期望时间内进入循环。如图(从oi wiki上搬的)

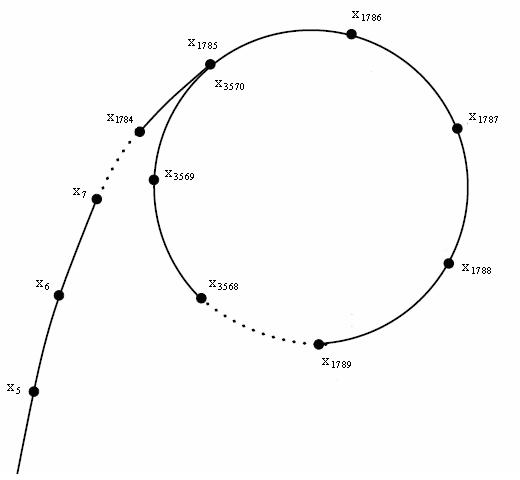
Pollard-rho1

从而可以通过重环找出\(f(y)\equiv f(x) (mod\ n) \Rightarrow y\equiv x (mod\ n)\)

如何判断环呢？

Floyd 判环，Brent 判环,倍增优化。与数论无关所以不进行展开了

详细见代码:

//素数测试与因式分解 

// 快速乘
ll qmul(ll a, ll b, ll m) {
    return static_cast<__int128>(a) * b % m;
}

// 快速幂：计算 (a^b) % m，使用快速乘进行模幂运算
ll qpow(ll a, ll b, ll m) {
    ll res = 1 % m;          
    for (; b; b >>= 1) {     
        if (b & 1)           
            res = qmul(res, a, m);
        a = qmul(a, a, m);  
    }
    return res;
}

// Miller-Rabin素数检测，确定n是否为素数,O(slog(n))
bool isprime(ll n) {
    if (n < 2)
        return false;
    static constexpr int A[] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
    int s = __builtin_ctzll(n - 1);  
    ll d = (n - 1) >> s;             

    for (auto a : A) {                
        if (a == n)    return true;
        ll x = qpow(a, d, n);       // 计算a^d mod n
        if (x == 1 || x == n - 1)   continue;		//通过
        bool ok = false;
        for (int i = 0; i < s - 1; ++i) {
            x = qmul(x, x, n);        
            if (x == n - 1) {       // 若得到n-1，则通过本轮
                ok = true;
                break;
            }
        }
        if (!ok)                     // 所有次平方后仍未通过，n为合数
            return false;
    }
    return true;                    // 所有基数测试通过，n为素数
}

// 因数分解函数，返回n的所有质因数（排序后）
vector<ll> factorize(ll n) {
    vector<ll> p;                    // 存储质因数

    function<void(ll)> f = [&](ll n) {
        if (n <= 10000) {
            for (int i = 2; i * i <= n; ++i)
                while (n % i == 0) {
                    p.push_back(i);
                    n /= i;
                }
            if (n > 1)						
                p.push_back(n);
            return;
        }
									// 若n为质数，直接加入结果
        if (isprime(n)) {
            p.push_back(n);
            return;
        }
        // Pollard's Rho算法寻找因数
        auto g = [&](ll x) {        // 伪随机生成函数
            return (qmul(x, x, n) + 1) % n;
        };
        ll x0 = 2;                  // 初始值
        while (1) {
            ll x = x0, y = x0, d = 1;
            ll qpow = 1, lam = 0;
            ll v = 1;
            // 使用Brent判环+倍增优化寻找非平凡因数
            while (d == 1) {
                y = g(y);           // y步进两次
                ++lam;
                v = qmul(v, abs(x - y), n);  // 累积差值乘积
                if (lam % 127 == 0) {
                    d = gcd(v, n);
                    v = 1;
                }
                // 当达到当前qpow时，更新x并检查
                if (qpow == lam) {
                    x = y;
                    qpow *= 2;     // 倍增步数上限
                    lam = 0;
                    d = gcd(v, n);
                    v = 1;
                }
            }
            // 找到非平凡因数d，递归分解d和n/d
            if (d != n) {
                f(d);
                f(n / d);
                return;
            }
            ++x0;                   // 重新选择初始值
        }
    };
    f(n);                           // 开始分解
    sort(p.begin(), p.end());       // 排序质因数
    return p;
}

快速求阶乘取模

快速解决\(n! \% p = ?\)的方法。

数据规模比较大（\(>1e6\)）时用多项式解决，快速阶乘算法

比较小时，可以转化为模数为素数整数幂\(p^\alpha\)再用中国剩余定理合并。

将阶乘\(n!\)的所有因子都提取出来，进而得到分解,\((n!)_p\)表示在阶乘\(n!\)的结果中去除所有\(p\)的幂次得到的整数:

\[n!=p^{\nu_p(n!)}(n!)_p \]

先求\((n!)_pmod\ p^\alpha\)

递推公式：

1.对于素数\(p\)和正整数\(n\),有 \((n!)_p\equiv (-1)^{\lfloor n/p\rfloor}\cdot(n\bmod p)!\cdot(\lfloor n/p\rfloor!)_p\pmod{p}.\)

2.对于素数\(p\)和正整数\(\alpha,n\),有 \((n!)_p\equiv (\pm 1)^{\lfloor n/p^\alpha\rfloor}\cdot\left(\prod_{\substack{1\leq j\leq (n\bmod p^\alpha),\ j\perp p}}j\right)\cdot(\lfloor n/p\rfloor!)_p\pmod{p^\alpha}.\) 其中，\(\pm 1\)的取值如同Wilson定理的推广。

结果：

对于素数\(p\)和正整数\(\alpha,n\),有 \((n!)_p\equiv (\pm 1)^{\sum_{j\geq\alpha}\lfloor n/p^j\rfloor}\prod_{j\geq 0}F(\lfloor n/p^j\rfloor\bmod p^\alpha),\) 其中，\(F(m)=\prod_{\substack{1\leq k\leq m,\ k\perp p}}k\bmod p^\alpha\)且\(\pm 1\)的取值与上文所述相同。

再求\(\nu_p(n!)\)

Legendre 公式：

对于正整数\(n\),阶乘\(n!\)中含有的素数\(p\)的幂次\(\nu_p(n!)\)为 \(\nu_p(n!)=\sum_{i=1}^\infty\left\lfloor\frac{n}{p^i}\right\rfloor=\frac{n-S_p(n)}{p-1}\)

其中，\(S_p(n)\)为\(p\)进制下\(n\)的各个数位的和。特别地，阶乘中2的幂次是\(\nu_2(n!)=n-S_2(n)\)。

Kummer 定理 :

素数\(p\)在组合数\(\binom{m}{n}\)中的幂次，恰好是\(p\)进制下\(m\)减掉\(n\)需要借位的次数，亦即

\[\nu_p\left(\binom{m}{n}\right)=\frac{S_p(n)+S_p(m-n)-S_p(m)}{p-1}. \]

特别地，组合数中2的幂次是\(\nu_2\left(\binom{m}{n}\right)=S_2(n)+S_2(m-n)-S_2(m)\)。

BSGS算法

求解\(a^x\equiv b\pmod{m}\)的离散对数问题

\((a,m)=1\)时有：

设\(x=i*t-j\),其中\(t=\lfloor\sqrt{p}\rfloor,0\leq j\leq t-1\),则方程变为\(a^{i*t-j}\equiv b\pmod{p}\).

即\((a^t)^i\equiv b*a^j\pmod{p}\). 对于所有的\(j\in[0,t-1]\),把\(b*a^j\mod p\)插入一个Hash表。 枚举\(i\)的所有可能取值，即\(i\in[0,t]\),计算出\((a^t)^i\mod p\),在Hash表中查找是否存在对应的\(j\),更新答案即可。

时间复杂度为\(O(\sqrt{p})\)。

点击查看代码 
ll bsgs(ll a,ll b, ll p){
    unordered_map<ll,ll> mp;mp.clear();
    b %=p;
    ll t = (ll)sqrt(p)+1;
    for(ll j=0;j<t;j++){
        ll val = 1ll*b*qpow(a,j,p)%p;
        mp[val]=j;
    }
    a = qpow(a,t,p);
    if(!a)return !b ? 1:-1;
    for(ll i=0;i<=t;i++){
        ll val = qpow(a,i,p);
        ll j = mp.find(val) == mp.end() ? -1:mp[val];
        if(j>=0 && i*t-j>=0)return i*t-j;
    }
    return -1;
}

\((a,m) \neq 1\)，有扩展大步小步算法（利用同余的除法即可）

点击查看代码 
#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using ll = long long;
using i128 = __int128;
using namespace std;

int gcd(int a, int b){return b ? gcd(b,a%b) : a;}

i128 qpow(i128 a,i128 b,i128 mod){
	i128 res = 1;
	while(b){
		if(b&1) res = res*a %mod;
		a = a*a %mod;
		b >>= 1;
	}
	return res;
}

ll bsgs(ll a, ll b, ll p, ll ad) {
    unordered_map<int,int> mp;
    mp.clear();
    ll t = ceil(sqrt(double(p))) + 1;
    for (ll r = 0, sum = b % p; r < t; ++ r) {
        mp[sum] = r; //直接赋值即可，不必比较大小
        sum = 1ll * sum * a % p;
    }
    ll at = qpow(a, t, p), sum = ad;
    for (ll q = 0; q <= t; ++ q) {
        if (mp.count(sum)) {
            if (1ll * q * t - mp[sum] >= 0ll) {
                return 1ll * q * t - mp[sum]; 
            }
        }
        sum = 1ll * sum * at % p;
    }
    return - 1;
}
ll exbsgs(ll a, ll b, ll p) {
  a %= p, b %= p;
  if (b == 1 || p == 1) return 0;
 
  ll k = 0, d, ad = 1;
  while ((d = (gcd(a, p))) != 1) {
    if (b % d) return - 1;
    k ++; 
    b /= d, p /= d;
    ad = (1ll * ad * a / d) % p;
    if (ad == b) return k;
  }
  ll ans = bsgs(a, b, p, ad);
  if (ans == - 1) return - 1;
  return ans + k;
}

void solve(){
    int a,p,b;
        while(cin>>a>>p>>b){
        if(a==0&&b==0&&p==0)return;
        int l=exbsgs(a,b,p);
        if(l==-1)cout<<"No Solution"<<endl;
        else cout<<l<<endl;
    }
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int tt =1;
    // cin>>tt;
    while (tt--)solve();
    return 0;
}

杜教筛

处理数论函数前缀和的问题
Define \(S(n) = \sum ^n _{i=1}f(i)\)

we can get \(\sum_{i=1}^{n}(f*g)(i) =\sum_{i=1}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)\)

\(g(1)S(n)=\sum_{i=1}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)-\sum_{i=2}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)\) \(=\sum_{i=1}^{n}(f*g)(i)-\sum_{i=2}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)\)

假如我们可以构造恰当的数论函数 \(g\) 使得：

  1. 可以快速计算 \(\sum_{i=1}^{n}(f*g)(i)\); 2
  2. 可以快速计算 \(g\) 的前缀和，以用数论分块求解 \(\sum_{i=2}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)\)。 则我们可以在较短时间内求得 \(g(1)S(n)\)
// 记忆化结果（杜教筛）
unordered_map<int, ll> fMu;
unordered_map<int, ll> fPhi;


// 最小质因子、素数列表、欧拉函数、莫比乌斯函数前缀和、欧拉函数前缀和
vector<int> minp, primes, phi, mu;
vector<ll> sphi;

const int N = 1e6; // 预处理的最大范围，可根据题目调整

//线性筛：筛出最小质因子、欧拉函数 phi、莫比乌斯函数 mu的前缀和

void sieve(int n) {
    // 初始化数组
    minp.assign(n + 1, 0);     // minp[i] 表示 i 的最小质因子
    phi.assign(n + 1, 0);      // 欧拉函数 φ(i)
    mu.assign(n + 1, 0);       // 莫比乌斯函数 μ(i)
    primes.clear();            // 存储所有质数

    phi[1] = 1;                // φ(1) = 1
    mu[1] = 1;                 // μ(1) = 1

    for (int i = 2; i <= n; ++i) {
        if (minp[i] == 0) {    // i 是质数
            minp[i] = i;       // 最小质因子就是它自己
            phi[i] = i - 1;    // φ(p) = p - 1
            mu[i] = -1;        // μ(p) = -1
            primes.push_back(i);
        }

        // 枚举已知的质数 p，筛去 i * p
        for (auto p : primes) {
            if (i * p > n) break;
            minp[i * p] = p;

            if (p == minp[i]) { // i 能被当前质数 p 整除，说明 i * p 有重复质因子
                phi[i * p] = phi[i] * p; // φ(i*p) = φ(i) * p
                mu[i * p] = 0;           // 有平方因子，μ=0
                break;
            } else {                     // i 和 p 互质
                phi[i * p] = phi[i] * (p - 1); // φ(i*p) = φ(i)*φ(p) = φ(i)*(p-1)
                mu[i * p] = -mu[i];            // μ(i*p) = -μ(i)
            }
        }
    }

    // 计算前缀和：sphi[i] = φ(1)+φ(2)+...+φ(i)
    sphi.resize(n + 1);
    for (int i = 1; i <= n; ++i) {
        sphi[i] = sphi[i - 1] + phi[i];
        mu[i] += mu[i - 1];  // mu 数组改为前缀和形式：mu[i] = μ(1)+μ(2)+...+μ(i)
    }
}


//算 f 前缀和的函数
ll sumMu(int n) {
    if (n <= N) return mu[n];   // 小于等于预处理范围，直接返回
    if (fMu.count(n)) return fMu[n]; // 已经计算过，直接返回缓存值
    // 算 f * g 的前缀和，储存到ans里
    ll ans = 1; // 初始为 S(1) = 1

    // 分块处理g
    for (int l = 2, r; l <= n; l = r + 1) {// 注意从 2 开始
        r = n / (n / l); // 找到相同商值的右边界
        ans -= (ll)(r - l + 1) * sumMu(n / l); // 应用杜教筛公式
    }

    return fMu[n] = ans; // 缓存结果
}

ll sumPhi(int n){
    if(n<=N)return sphi[n];
    if(fPhi.count(n))return fPhi[n];
    ll ans = 1ll*(n)*(n+1)/2;

    for(int l=2,r;l<=n;l=r+1){
        r=n/(n/l);
        ans-=(ll)(r-l+1)*sumPhi(n/l);
    }
    return fPhi[n]=ans;
}


杂项

求整系数方程的整数解

\(a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\) 是一个整数系数多项式且 \(a_0, a_n\) 都不是零，则其可能存在的有理根只能是以 \(a_0\) 的因数作分子以 \(a_n\) 的因数作分母的既约分数。

这可以帮助我们更快的得到方程的解（用整除可以证明）

是否存在有理根需要用艾氏判别法。

给出下面的整系数多项式f(x)\(=a_n+a_{n-1}x^{n-1}+…+a0\)

如果存在素数p，使得p不整除\(a_n\) ，但整除其他\(a_i\),(i=0,1,...,n-1) ；

p² 不整除\(a_0\)

那么f(x) 在有理数域上是不可约的。

从初中小蓝本上学的，令人感慨。


取整函数

来源:初等数论(闵嗣鹤、严士健)

定义:函数\([x]\)与\(\{x\}\)是对于一切实数都有定义的函数，函数\([x]\)的值等于不大于\(x\)的最大整数。

函数\(\{x\}\)的值是\(x-[x]\)。我们把\([x]\)叫做\(x\)的整数部分，\(\{x\}\)叫做\(x\)的小数部分。

由定义可以立刻得出下列简单性质：

I \(x=[x]+\{x\}\).

II \([x]\leq x<[x]+1\), \(x-1<[x]\leq x\), \(0\leq\{x\}<1\).

III \([n+x]=n+[x]\), \(n\)是整数.

IV \([x]+[y]\leq[x+y]\), \(\{x\}+\{y\}\geq\{x+y\}\).

V \([-x]=\begin{cases}-[x]-1, & \text{当 } x \text{ 不是整数时}, \\ -[x], & \text{当 } x \text{ 是整数时}.\end{cases}\)

VI （带余数除法）若\(a,b\)是两个整数，\(b>0\)，则\(a=b\left[\frac{a}{b}\right]+b\left\{\frac{a}{b}\right\}\), \(0\leq b\left\{\frac{a}{b}\right\}\leq b-1\).

VII 若\(a,b\)是任意两个正整数，则不大于\(a\)而为\(b\)的倍数的正整数的个数是\(\left[\frac{a}{b}\right]\).

另外有：

1.\(\left[\frac{x}{m}\right]=\left[\frac{[x]}{m}\right] \Rightarrow \left[\frac{x}{m^2}\right]=\left[\frac{[\frac{x}{m}]}{m}\right]\)

2.组合数一定是整数\(\Rightarrow\)连续的\(k\)个整数的乘积必然被\(k!\)整除。


数论分块

数论分块的过程大概如下：考虑和式 \(\sum_{i=1}^{n} f(i) \left\lfloor \frac{n}{i} \right\rfloor\)

那么由于我们可以知道 \(\left\lfloor \frac{n}{i} \right\rfloor\) 的值成一个块状分布（就是同样的值都聚集在连续的块中），那么就可以用数论分块加速计算，降低时间复杂度。

利用上述结论，我们先求出 \(f(i)\) 的 前缀和（记作 \(s(i) = \sum_{j=1}^{i} f(j)\)），然后每次以 \([l, r] = \left[l, \left\lfloor \frac{n}{\left\lfloor \frac{n}{i} \right\rfloor} \right\rfloor\right]\) 为一块，分块求出贡献累加到结果中即可。

void solve(){
    int n,k;cin>>n>>k;
    int ans =0;
    int j=0;
    for(int i=1;i<=n;i=j+1){
        if(k/i==0)break;		
        j = k/(k/i);					//块的右边界
        if(j>n)j=n;					//块的范围出界
        ans += (j-i+1)*(i+j)/2*(k/i);
    }
    cout<<n*k-ans;
}

莫比乌斯反演

感觉反演一般是增添一个求和号之后再交换求和顺序，以退为进简化问题？

函数的方式我们称为正演，则的方式便是反演 只有莫比乌斯反演是数论中的知识,接下来只介绍莫比乌斯反演

莫比乌斯函数

\(\mu\)为莫比乌斯函数，定义为 $$ \mu(n)=\begin{cases}1&n=1\0&n\text{含有平方因子}\(-1)^k&k\text{为}n\text{的本质不同质因子个数}\end{cases} $$

有结论：

\[\sum_{d|n}\mu(d)=[n=1] \]

\[\sum_{d|\gcd(i,j)}\mu(d)=[\gcd(i,j)=1] \]

\[g(x)=\sum_{d|n}f(d)\Leftrightarrow f(x)=\sum_{d|n}\mu\left(\frac{n}{d}\right)g(d) \]

利用这些知识可以简化一些gcd相关的运算，具体运用还是看题目

题库


贝特勒猜想

在正整数\(m,2m\)之间一定有一个质数（已被切比雪夫证明）


费马分解

若\(n\)为一个正奇数，则存在一个一对一的方式（也就是可以相互转换）令其等于两个正整数平方的差。

$n = ab = s^2 - t^2, \quad s = \frac{a + b}{2}, \quad t = \frac{a - b}{2} \tag{4.7.1} $ （因为 \(a, b\) 都是奇数所以 \(s, t\) 为整数）

反过来，若已知 \(n = s^2 - t^2\)，我们可以将 \(n\) 分解为 \(n = (s - t)(s + t)\)（平方差公式），所以是一个一对一的变换。

那怎么找这两个数 \(s, t\) 呢？

因为 \(n = x^2 - y^2\)，我们需要找一个可以写成 \(x^2 - n\) 形式的平方数。所以我们从下面这个数列里找 $$ t^2 - n, (t + 1)^2 - n, (t + 2)^2 - n $$ 其中 \(t\) 为大于 \(\sqrt{n}\) 的最小整数。

这个搜索一定会结束，因为 \(n = 1 \cdot n\) 这种情况会给出最后的解 $$ n = \left(\frac{n + 1}{2}\right)^2 - \left(\frac{n - 2}{2}\right)^2 $$


费马数 (Fermat Number)

形如 \(F_n = 2^{2^n} + 1\) 的数。

梅森数 (Mersenne Number)

形如 \(M_p = 2^p - 1\) 的数，其中 $ p $ 为素数。

而\(M_p\)为素数时，我们称其为梅森素数。

下面性质来源https://zhuanlan.zhihu.com/p/82356370，证明请看原知乎

1.若\(n\)为合数，则\(M_n\)为合数。

2.\(n\)为大于1的奇数时，\(M_n\)的所有因子形式为\(8k-1\)或\(8k+1\)

3.\(p\)为奇素数时，\(M_p\)的所有素因子可表示为\(2kp+1\)的形式。

4.若素数\(p\equiv3(mod\ 4)\), 则\(2p+1\)是素数的充要条件是\(2^p\equiv1(mod\ 2p+1)\)

5.正整数\(n\)是一个偶完全数当且仅当\(n=2^{p-1}M_p\)，\(M_p\)是梅森素数。

6.若\(n>1\)，则\(M_n\)不可能为一个正整数的高次幂。

更多性质请查找相关文献


复数的gcd

来源:基础数论学习笔记（3）- Gcd and Bezout's Identity 最大公约数与裴蜀定理

两个不同时为 0 的复数 \(a, b\) 的最大公约数为复数 \(d\)，其同时整除 \(a, b\) 且 \(d\overline{d}\) 最大，写法同样为 \((a, b)\)

  • 若 \(d \mid a, d \mid b\) 则 \(-d, \pm id, \pm d \pm \overline{d} = \pm id \pm i\overline{d}\) 也都同样满足（也就是复数的 gcd 不具有唯一性）

计算 \((3 + i, 4i)\)

解：设 \(d \mid 3 + i, d \mid 4i\)，则 \(d \mid (3 + i)(3 - i) = 10\)，且 \(d \mid (4i)(-4i) = 16\)，所以 \(d \mid 2\)

  • \(2 = (1 - i)(1 + i)\)

  • \(d\) 一定整除 \(4i - (3 + i) = -3 + 3i = 3(i - 1)\) 这说明 \(d \in \{i - 1, -i + 1, -1 - i, 1 + i\}\)


复数的整除

来源:基础数论学习笔记（1）- Divisibility 整除

考虑 \(\mathbb{Z}[i] = \{a + bi, a, b \in \mathbb{Z}\}\) 其中 \(i^2 = -1\)，若 \(a, b\) 都属于 \(\mathbb{Z}[i]\) 且 \(b \neq 0\)，则在 \(\mathbb{Z}[i]\) 中存在 \(q\) 和 \(r\)

满足： $ a = qb + r, \quad 0 \leq r\overline{r} \leq \frac{b\overline{b}}{2} \tag{1.4} $

用法:复数除法加取整就行


循环小数

定义 如果对于一个无限小数\(0.a_1a_2\cdots a_n\cdots,(a_n\)是0,1,\(\cdots\),9之中的一个数码,并且从任何一位以后不全是0)能找到两个整数\(s\geq 0,t>0\)使得 \(a_{s+i}=a_{s+kt+i},i=1,2,\cdots,t;k=0,1,2,\cdots.\) 我们就称它为循环小数，并简单地把它记作\(0.a_1a_2\cdots a_s\dot{a}_{s+1}\cdots \dot{a}_{s+t}\)。

对于循环小数而言，具有上述性质的\(s\)及\(t\)是不只一个的。

如果找到的\(t\)是最小的，我们就称\(a_{s+1},a_{s+2},\cdots,a_{s+t}\)为循环节；\(t\)称为循环节的长度；若最小的\(s=0\)，那小数就叫做纯循环小数，否则叫混循环小数。

性质：

  • 有理数\(\frac{a}{b},0<a<b,(a,b)=1\),能表成纯循环小数的充分与必要条件是\((b,10)=1\)。
  • \(\frac{a}{b}\)是有理数，其中\((a,b)=1,0<a<b,b=2^{a_1}5^{a_2}\)。\(a_1,a_2\)不全为0。那么\(\frac{a}{b}\)必然可以转换为有限小数。
  • 定理3 若\(\frac{a}{b}\)是有理数，其中\(0<a<b,(a,b)=1,b=2^\alpha5^\beta b_1,(b_1,10)=1,b_1\neq 1,\alpha,\beta\)不全为零，则\(\frac{a}{b}\)可以表成混循环小数，其中不循环的位数是\(\mu=\max(\alpha,\beta)\)(即\(\alpha,\beta\)中之较大者).
posted @ 2025-04-22 22:03  Tenryon  阅读(87)  评论(0)    收藏  举报