做题随笔：P10778

Solution

本篇题解给出了思考过程，不是单纯拿结论水题解的呢！

题意

原题链接

给定简单无向图，\(q\) 次强制在线询问，每次割掉 \(k(k \leq 15)\) 条边，询问图的连通性。

分析

首先我们可以只考虑初始是连通图的情况，不然怎么割都是不连通的，就不用写了，特判一个就彳亍。（好吧事实上好像初始就是连通图）

如果不强制在线，挂上线段树，分治一下高高兴兴 100pts。

但是很可惜，强制在线。那么我们考虑一下如何删边会导致图不连通。

1.只割两条边

我们先考虑一个简化后的问题：假如只割两条边怎么判？

首先，一个比较经典的想法是：先跑出一个 dfs 生成树。两条边中至少有一条是树边（不然生成树就可以让图连通）。我们先假设图中没有桥，下面进行讨论：

下文中的某非树边“覆盖”树边指该非树边和树边在同一个环内。

1. 若一条是树边，一条是非树边：要求这条非树边是唯一覆盖这条树边的非树边；
2. 若两条都是非树边：要求覆盖两条树边的非树边集合相同。

1 很显然，直接断开了。大概解释一下 2：

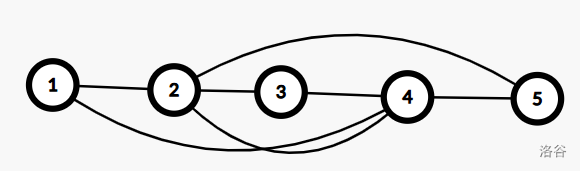
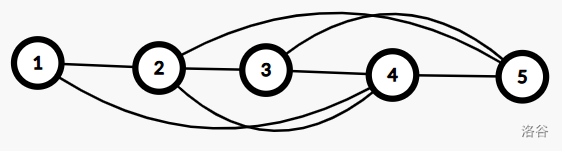
比如这样的情况，删去树边 \((2,3),(3,4)\)，上面的图中，覆盖两条树边的非树边集合相同，故没有任何一条非树边不经过两树边连接了中间的点，所以删去后 3 会成一个单独的连通块，图变得不连通。

其他情况是同理的，可以自己再画几种情况试试。

如果认为一条覆盖一条非树边的非树边集合是它自身，那么我们“只需”维护覆盖每条边的非树边集合，删边的时候判断两条边的集合是否相同即可。更具实操性一点地，我们考虑对每条非树边进行编号，用一个 bitset 维护某编号的边是否在集合内。然鹅还是不行（毕竟边太多了）。

于是，我们请出随机化！给每条非树边一个随机权值，树边的权值是所有覆盖它的非树边权值的异或和。于是删边时，我们只需判断两条边的权值是否相等，或者说异或和是否为 0 即可。

为什么这样是正确的呢？其实是可能错误的，但是概率极小。我们考虑两个非树边集合 A，B 中的边不同，但是异或和为 0 的情况：

先扔掉两个集合中所有相同的边，因为它们异或之后本就应该是 0。我们先假设扔完之后只有 A 比 B 多一条边 \(e_1\)，则要求这条边的权值是 0，在使用 unsigned long long 进行随机权值的时候，概率为 \(\dfrac{1}{2^{64}}\)。若 A 还多了一条边 \(e_2\)，则要求这条边和 \(e_1\) 相同，概率仍为 \(\dfrac{1}{2^{64}}\)。同理，多 \(k\) 条边，则要求 \(e_k\) 权值与前 \(k-1\) 条的异或和相同，概率不变。

再考虑 B 中有一条不同于 A 中所有边的边，同理，则要求 B 中这条边的权值与 A 中多出来的边权值异或和相等。同理可以推广到任意条。

所以我们证明了：两个边集不同但是权值相同的概率是 \(\dfrac{1}{2^{64}}\)，完全不影响正确性，大胆写吧！

2.完整问题

那么现在我们想想要割更多边使图不连通可以怎么做。仿照上面的思路，有：

1. 割掉的边集中存在一条树边和覆盖它的所有非树边；
2. 割掉的边集中存在某个子集，在原图中删去子集中的非树边后，剩下的每条非树边都对子集中的的偶数条树边进行了覆盖。

1 仍旧显然，对 2 进行一下感性的解释：

比如下图情况：

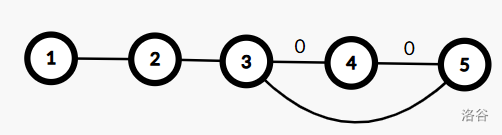
我们先按删两条边使图不连通的方式，删掉 \((3,4),(4,5)\)（上面的 0 表示删除），发现 4 断开了。如果我们想要图连同，只需存在一条由其他点到 4 的边，比如 \((2,4)\)。

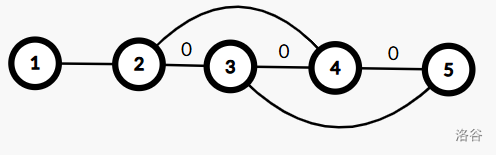
随后你发现，若再删去 \((2,3)\)，图不连通。并且，此时删去的树边满足 2。

参照上面的思路，大概可以归纳地证明一下：删除树边数量等于二的时候，显然成立，删去树边后产生一个新的连通块，其中某一节点为 \(u\)。然后反证：若图连通，必然存在一条非树边连接了两 \(u\) 和另一连通块的 \(v\)。此时要求 \(u,v\) 非树边覆盖的 \(v\) 连通块中树边路径连通，此时 \(u,v\) 只覆盖奇数条删除的树边。要使图不连通，则在 \(u,v\) 非树边覆盖的 \(v\) 连通块中树边路径中删去一边，或直接删去这条非树边。此时满足条件。

大概这样，有点抽象。（本蒟蒻水平有限，说不太清楚，嘤嘤嘤~）

注意到以上两种情况等价于选出边集存在异或和为 0 的子集。可以使用异或线性基解决。关于随机异或的概率问题，对于 1 情况概率同上；对于 2 情况，\(k \leq 15\)，至多有 \(2^{15}\) 种子集异或和的取值，不应为 0 但是可以生成 0 的概率不大于 \(\dfrac{2^{15}}{2^{64}}=\dfrac{1}{2^{49}}\)，仍然十分优秀。

最后一个问题：怎么具体确定一条非树边覆盖了哪些边？

由于我们跑的是 dfs 生成树，非树边只有返祖边（从深度大的点连到深度小的点的非树边），所以非树边一定是在这个环的最深处被访问的。访问到的时候给权值，回溯的时候一路带上去就可以了。

复杂度 \(O(n+\omega \sum k)\)，其中 \(\omega = 64\)。

（快得感觉像是假的）

Code

#include <iostream>
#include <cstdio>
#include <cctype>
#include <cstdlib>

typedef long long ll;

ll fr() {
	ll x=0;char c=getchar();
	while(!isdigit(c)) c=getchar();
	while(isdigit(c)) {
		x=(x<<3)+(x<<1)+(c^48);
		c=getchar();
	}
	return x;
}

const int maxn=1.1e5;
const int maxm=1.1e6;

int head[maxn],tot=0;

struct edge{
	int nxt,to,x;
}e[maxm];

void ade(int u,int v,int tag) {
	e[++tot].to=v;
	e[tot].nxt=head[u];
	e[tot].x=tag;
	head[u]=tot;
}

int n,m,k;
ll d[maxn],val[maxm];
bool vis[maxn];

ll rand64() {
	return ( (1ll * (std::rand() & 0xFFFF)) << 48 ) |
	( (1ll * (std::rand() & 0xFFFF)) << 32 ) |
	( (1ll * (std::rand() & 0xFFFF)) << 16 ) |
	( (1ll * (std::rand() & 0xFFFF)) );
}

void dfs(int u,int f) {
	vis[u]=1;
	for(int i = head[u]; i; i=e[i].nxt) {
		int v=e[i].to,id=e[i].x;
		if(v==f) continue;
		if(!vis[v]) {dfs(v,u);d[u]^=d[v];val[id]=d[v];}
		else if(!val[id]) {val[id]=std::rand();d[u]^=val[id];d[v]^=val[id];}
	}
}

bool insert(ll *p,ll x) {
	for(int i=63;~i;i--){
		if(x>>i&1){
			if(p[i]) x^=p[i];
			else {p[i]=x;return 1;}
		}
	}
	return 0;
}

int xo;

int main() {
	std::srand(20250725);
	n=fr(),m=fr();
	for(int i = 1; i <= m; i++) {
		int u=fr(),v=fr();
		ade(u,v,i);
		ade(v,u,i);
	}
	k=fr();
	dfs(1,0);
	while(k--) {
		int c=fr();
		bool ans=1;
		ll p[64]={0};
		while(c--) {
			int id=fr()^xo;
			if(!insert(p,val[id])) ans=0;
		}
		printf("%s\n",ans?"Connected":"Disconnected");
        xo+=ans;
    }
	return 0;
}

一些闲话

当时蒟蒻自己学的时候就觉得很诡异，直至今日自己写题解大概证了一下，才感觉合理多了。只能说随机化属于是人类智慧的巅峰了。

（现在才发现已经写了这个题好久了啊 awa）

如果觉得有用，点个赞吧！