做题随笔：P13308

Solution

题意

原题链接

维护一颗 \(n\) 层的满二叉树，支持删边、查询节点所在连通块大小。

场上看到题面我先笑了，看到数据范围差点似了。\(2^{60}\) 个点干翻一切（大雾）。

分析

一个很直接的想法：建图，每次断边向子树和父亲 dfs 更新连通块大小，其他都不想，空间早炸了。所以要么找一种方法，不建图而维护这棵树；要么只建一部分。本蒟蒻这里就只维护了断过边的点。

回归问题，那么现在要解决两个问题——

1. 怎么表示断边？
2. 怎么判断连通块大小？

我们先假设可以建出整个图：

对于第一个问题，我们可以简单地打标记。本蒟蒻直接依照题意，在点上标记表示它与父亲断开。

对于第二个问题，我们有一个想法：在断掉的完整子树里，连通块大小就是子树大小；在不完整子树里，连通块大小是 \(1\) 加上左右子树大小（断掉的子树 sz 即为 \(0\)）。（如图）

具体地：我们可以从根往下走到查询节点，沿途记录最后一个被打过标记的节点，该标记节点的 sz 即为所求连通块大小。

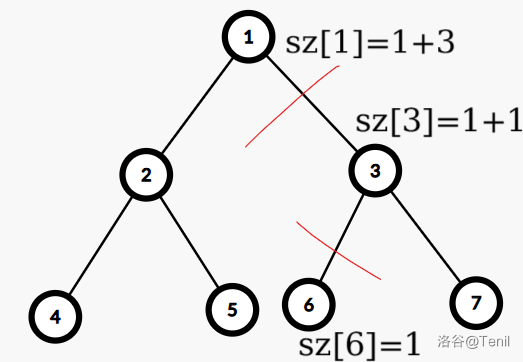
按上文，我们建个线段树直接维护 sz 和 tag 就可以了。

想法很简单，做法很自然，但是你的 \(2^{60}\) 会花生。

这时候我们会发现：操作涉及的节点数远小于树上总节点数，除了涉及的点，其他点都是无效的（例如：上图 \(2\) 的这棵子树未被更改，其 sz 可以直接根据 dep 获取）。这就启发我们：可以考虑线段树动态开点的方式，只把有效的点建出来（从根到断边的点的一条链），以减少复杂度。

于是我们在一颗依托于原满二叉树的动态开点线段树上维护节点信息，每次断边时找出一条链，分配子树大小和标记即可。

落到实现上，最后有一个问题：怎么判断一个点在左树还是右树？我有一个 \(O(\log n)\) 的脑瘫写法，够用就行：

int son(ll p,ll f) {
	ll l=f*2,r=f*2+1;
	while(!(l<=p&&p<=r)) {
		l*=2,r=r*2+1;
	}
	ll md=l+r>>1;
	return p<=md?1:2;
}

于是本蒟蒻成功 A 掉，成为机房除了省队以外唯一 A 的人（喜）。

实现 & 分步 Code

动态开点线段树维护子树大小和标记；

向上维护：\(sz(p)=1+sz(ls)+sz(rs)\)，如果某儿子 \(tag=1\) 则不加。

void pp(ll p,ll size) {
//传入的 size 是满二叉树对应子树的大小
	sz[p]=1;
	sz[p]+=ls?(tag[ls]?0:sz[ls]):(size>>1)-1;
	sz[p]+=rs?(tag[rs]?0:sz[rs]):(size>>1)-1;
//如果儿子对应的点都还没有建出来，那就是满二叉树上的对应点
}

修改：找一条（没有就建）到指定节点的链，到指定节点打标记（因为要判断子树方向，修改和查询都是 \(O(\log^2 n)\) 的）；

void cg(ll p,ll size,ll x,ll aim) {
//p:当前节点，x:对应满二叉树上的节点
	if(x==aim) {
		tag[p]=1;
		return;
	}
	int dir=son(aim,x);
	if(dir==1) cg(ls?ls:New(p,1,size),size>>1,x<<1,aim);
	else cg(rs?rs:New(p,2,size),size>>1,x<<1|1,aim);
	pp(p,size);
}

查询：从根向下走，如果目标点没建出来或建出来了但没标记，则返回最后一个经过的标记点的 sz；否则返回本节点 sz。

ll ask(ll p,ll x,ll aim,ll f) {
	if(x==aim) return tag[p]?sz[p]:sz[f];
	if(tag[p]) f=p;
	int dir=son(aim,x);
	if(dir==1&&ls) return ask(ls,x<<1,aim,f);
	else if(dir==2&&rs) return ask(rs,x<<1|1,aim,f);
	else return sz[f];
}

注意：节点编号要开 long long!!!

总复杂度 \(O(n \log^2 n)\)，但是常数小，可以通过。

闲话

看讨论区说正解是 trie，倒回来看自己的解法其实和 trie 建树很像，也许这就是呢？

如果觉得有用，点个赞吧！