做题随笔：P10689

Solution

题意

原题链接

维护一个整数序列，要求能支持区间加，区间翻转，区间旋转（旋转 \(T\) 次即为将区间末尾 \(T\) 个数和前面的交换），在指定位置插入、删除，区间查询最小值。

区间长度 \(n \le 100000\)，操作次数 \(m \le 100000\)。

分析

ps：这里建议没写过 Splay 或 fhq-treap 的先做一下这道题。

维护序列的复杂操作（譬如本题的区间翻转）常用 Splay 或 fhq-treap，本题已经是明牌了。使用平衡树的原因是 BST 性质下，树进行 zig 或 zag 都不会改变其中序遍历的结果，从而可以在一棵树下同时维护序列顺序和最小值信息，且可以直接通过交换左右儿子的方式实现序列上的交换。

可以这么想：对于这种建在序列上的 BST，它初始排序依据的数据是数组角标，角标对应的具体数据只是附加信息，并且始终认为角标不变，用变动后的数据去对应角标。于是序列操作其实变成了在树上对角标和数据的对应关系进行改变。（如下图）

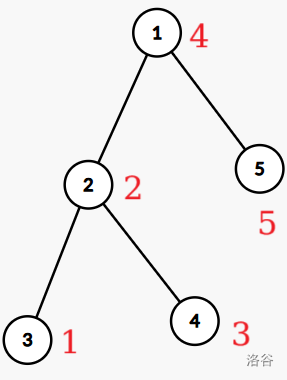
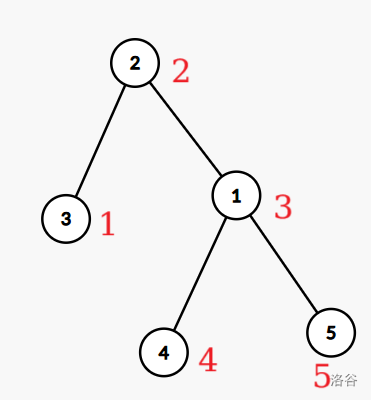
（红色表明中序遍历序，也即上文角标）原序列为 \(32415\)，经历平衡树的旋转后序列不变。

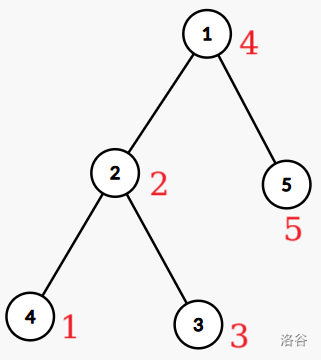
（对比上左图）而不通过旋转直接交换儿子后，序列为 \(42315\)。我们认为角标始终与中序遍历序对应，故直接交换实际交换了对应角标上的数字。区间交换同理。

实现&分步Code

本文假设您已经会写 Splay，不对数据结构本身进行说明，只说说用法。

0.建树

最简单粗暴的一个想法就是挨个插入，但是这样会 \(O(n\log n)\)，令人不适。可以考虑类似线段树建树一样，直接建出一颗完全二叉树：

void build(int l,int r,int &id) {
	if(l>r) return;
	int mid=(l+r)>>1;
	if(!id) id=New(a[mid]);
	build(l,mid-1,t[id].son[0]);
	if(t[id].son[0]) {
		t[id].min=std::min(t[id].min,t[t[id].son[0]].min);
		t[t[id].son[0]].f=id;
	}
	build(mid+1,r,t[id].son[1]);
	if(t[id].son[1]) {
		t[id].min=std::min(t[id].min,t[t[id].son[1]].min);
		t[t[id].son[1]].f=id;
	}
	upd(id);
	return;
}

或者直接建一条链然后一次伸展解决：

inline void build() {
	for(int i = 1; i <= n+2; i++) {
		cnt++;
		t[cnt].son[0]=rt;
		if(rt) t[rt].f=cnt;
		rt=cnt;
		t[cnt].val=a[i-1];
	}
	splay(rt,1);
	return;
}

本文使用第一种方法，并在链段添加了两个哨兵节点。

1.插入&删除

这其实是 BST 的模版操作，但是由于我们在树上维护的数据并不参与树上的排序（维护的是数据，排序依据是角标），又有一点不一样。本题要求在 \(A_x\) 之后插入、删除 \(A_x\)，实际上是在角标 \(x\) 后插入、删除角标 \(x\)，回到树上即：在排名为 \(x\) 的点后插入，删除排名为 \(x\) 的节点。

插入时，可以先找角标为 \(x\) 的节点 \(A\)，然后在它的右树找最小节点 \(B\)，这样 \(B\) 的左儿子位上就是空的，直接加点就行；删除逆向考虑一下，先找 \(x-1\)，再在它的右树上找第二小节点 \(A\)，这样 \(A\) 就有唯一左儿子对应角标 \(x\)，直接断掉。

其实这种类似“先找 xx，再找 xx，使某个节点为根的整个子树正好是操作区间”是本题的核心，建议画个图想想。

void insert(int v,int p) {
	loc(rt,v);loc(t[rt].son[1],1);
  //loc(rt,rank)：在以rt为根的子树下找排名为rank的节点并提到根上
	int x=t[rt].son[1];
	t[x].son[0]=New(p);
	t[cnt].f=x;
	return;
}

void remove(int v) {
	loc(rt,v-1);loc(t[rt].son[1],2);
	int x=t[rt].son[1];
	t[x].son[0]=0;
	return;
}

2.区间最小

首先解决“最小”：由于平衡树拿去维护角标了，所以数据的最小值并不能直接获得。但是我们再想想线段树，可以直接用节点维护最小值信息。这个其实相对好想，旋转的时候记得维护一下就好了。

inline void upd(int x) {
	t[x].size=1+t[t[x].son[0]].size+t[t[x].son[1]].size;
	t[x].min=std::min(std::min(
		t[t[x].son[0]].fix?t[t[x].son[0]].min:LONG_LONG_MAX,
		t[t[x].son[1]].fix?t[t[x].son[1]].min:LONG_LONG_MAX),
		t[x].val);
  //fix表示节点是否被使用，避免空节点的0错误更新
}

接下来问题就是“区间”了。类似删除的做法：先找角标为 \(x-1\) 的节点 \(A\)，然后在它的右树找排名为 \(y-x+2\) 的节点 \(B\)（\([x,n]\) 中第 \(y-x+2\) 大，即角标为 \(y+1\) 的点），这样的话 \(B\) 的左树上就是所有角标在 \([x,y]\) 的节点，查询左树根节点上维护好的 \(min\) 即可。

3.区间加、旋转、翻转

类似区间最小，区间加和翻转都可以简单的分出操作区间然后用懒标记维护了，相信这对于看完了上面的您来说并不难，这是代码：（其实你会发现这两个操作基本一模一样）

void optr(int x) {
	std::swap(t[x].son[0],t[x].son[1]);
	t[x].stag^=1;return;
}

void opta(int x,int k) {
  t[x].val+=k;
  t[x].min+=k;
  t[x].atag+=k;
}

void tagd(int x) {
	if(t[x].stag) {
		if(t[x].son[0]) optr(t[x].son[0]);//标记下放时一定要注意空节点
		if(t[x].son[1]) optr(t[x].son[1]);
		t[x].stag=0;
	}
	if(t[x].atag) {
		if(t[x].son[0]) opta(t[x].son[0]);
		if(t[x].son[1]) opta(t[x].son[1]);
		t[x].atag=0;
	}
	return;
}

void reverse(int l,int r) {
	loc(rt,l-1);loc(t[rt].son[1],r-l+2);
	int x=t[t[rt].son[1]].son[0];
	optr(x);tagd(x);splay(rt,x);
	return;
}

void add(int l,int r,int k) {
	loc(rt,l-1);loc(t[rt].son[1],r-l+2);
	int x=t[t[rt].son[1]].son[0];
	opta(x);tagd(x);splay(rt,x);
	return;
}

而区间旋转就相对棘手一点了。首先容易想到要先把 \(T\) 对 \(y-x+1\) 取模，因为 \(y-x+1\) 的正整数倍次数的旋转等于不转。设 \(T \bmod (y-x+1)=r\)，则操作变为交换 \([x,y-r]\) 和 \([y-r+1,y]\)。但是不可能找到一个它们的父亲能让他们直接交换，所以我们可以利用中序遍历根在左子树之后的性质，先分离出 \([x,y]\) 区间后，把 \(y-r\) 对应的节点提出来作为根，交换两个儿子后，将两个儿子合并到左儿子上，也就达成了目的。

int merge(int x,int y) {
	if(!x||!y) return x|y;
	loc(y,1);
	t[y].son[0]=x;
	t[x].f=y;
	upd(y);
	return y;
}

void revolve(int l,int r,int k) {
	loc(rt,l-1);loc(t[rt].son[1],r-l+2);
	int x=t[t[rt].son[1]].son[0];
	loc(x,r-l+1-k);//这里的r-l+1-k对应的就是上文 y-r，注意是子树内排名
	std::swap(t[x].son[0],t[x].son[1]);
	t[x].son[0]=merge(t[x].son[0],t[x].son[1]);
	t[x].son[1]=0;
	return;
}

4.注意事项

1. 有哨兵节点，排名记得先加一；
2. 一定不要对空节点做任何修改！！！
3. 找结点的时候每步都要伸展。

终于，你 AC 了！恭喜！

完整代码

闲话

蒟蒻经历了漫长的鏖战终于胜利，本篇算是一些写 BST 的理解了。

如果觉得有用，点个赞吧！