算法专题——Floyd拓展
Floyd算法概念
用于求解任意两点之间的最短路的算法,算法的原理本质为dp。下面进行简要的原理说明。
状态方程:dp[k][i][j]表示只经过前k个点,可以达到的i与j的最短路径为多少。那么不难得到转移方程:dp[k][i][j] = min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j])即从不经过k点与经过k点中得到一个最优的解。发现转移方程中k层的状态仅与k-1层的状态有关,因此我们可以使用滚动数组的方法进行空间上的优化,最终可以得到:dp[i][j] = min(dp[i][j], dp[i][k] + dp[i][k] + dp[k][j])。
求最短路
即Floyd最基本的应用,可用于求多源汇最短路,时间复杂度较大为O(n^3), 因此一般只能用于点数较少的情况. 这里不多赘述, 直接贴出代码, 自己体会.
for (int t = 1; t <= n; t++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dist[i][j] > dist[i][t] + dist[t][j])
dist[i][j] = dist[i][t] + dist[t][j];
例题
Cow Tours
题面:

分析:
连接一条边,使得两个联通块相连,并让得到的图的直径最小。
很显然枚举一下连接两个块的所有边,取得一个最小值即可,还要注意连接的边对于新得到的图的直径并没有贡献,而是原先两个图的直径的最大值。
给出核心代码
double MAX = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dist[i][j] != INF)
d1[i] = max(d1[i], dist[i][j]), MAX = max(MAX, d1[i]);
double ans = 0x3f3f3f3f;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dist[i][j] == INF) {
ans = min(ans, cal(i, j) + d1[i] + d1[j]);
printf("%.6f", max(ans, MAX));
求传递闭包
Floyd算法还可以求解原图的传递闭包, 这是非常显然的一个事实, 在求最短路的作用中, dist[i][j]的值为有效值时即表明了i含有一条路径可以到达j, 即可以连一条从i到j的边. 传递闭包相比于最短路的应用, 数组需要维护的数值更加简单, 只需要维护一个bool变量表明是否含有一条边可以从i指向j即可. 传递闭包的问题, 可以抽象为用于处理所有需要进行节点之间关系传递的问题, 如大小关系(A<B, B<C → A<C) .
例题
Sorting It All Out
题面:

分析:
分析给出的字符的大小关系,并依据大小关系将其打印出来。可以发现一个表达式给出时A<B,也表明了A会小于所有大于B的字符,即具有传递性,通过这种传递性我们可以得到整个序列的关系,当最终形成A < B < C < ... < E26个字符都出现的序列时,我们就表示这个序列是合法的,可以输出。这种传递性我们可以通过传递闭包进行实现,即通过确定字符之间的关系是否已经得到满足可以输出的情况,而要得到字符之间的关系就要时字符之间之间传递大小信息,即传递闭包的特点所在。
见核心代码:
for (int i = 1; i <= m; i++) {
scanf("%s", &line);
if (!flag) {
gra[line[0] - 'A'][line[2] - 'A'] = 1;
cnt ++;
for (int k = 0; k < n; k++)
for (int ii = 0; ii < n; ii++)
for (int jj = 0; jj < n; jj++)
gra[ii][jj] = gra[ii][k] & gra[k][jj];
flag = Check();
}
}
此外还有一种时间复杂度更低的写法,对于每次新加入的一条边,可以发现,添加的边数是O(n)级别的,仅与新加入的边的两个端点有关的点才会被更新。得到如下优化代码:
for (int i = 1; i <= m; i++) {
scanf("%s", &line);
if (!flag) {
gra[line[0] - 'A'][line[2] - 'A'] = 1;
cnt ++;
int u = line[0] - 'A', v = line[2] - 'A';
for (int ii = 0; ii < n; ii++) {
if (gra[ii][u]) gra[ii][v] = 1;
if (gra[v][ii]) gra[u][ii] = 1;
for (int jj = 0; jj < n; jj++)
if (gra[ii][u] && gra[v][jj]) gra[ii][jj] = 1;
}
flag = Check();
}
}
求最小环
可以得到一种朴素的思路。是否可以得到任意一个节点,假设其为环上的一点然后枚举另外两个节点,以其为环上另外两个点,而后通过min(g[i][j] + g[i][k] + g[k][j])得到最小环。核心代码见下。
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (g[i][j] + g[j][k] + g[k][i] < res) {
res = g[i][j] + g[j][k] + g[k][j];
getPath(i, j, k); //求以ijk确定的环经过的路径
}
这中思路十分简单明了,但是有一个毛病,即并不能通过i,j,k互通,得到i,j,k在一个环上,即不能通过三个点从而确定一个环。
但是可以发现,如果i,j,k可以确定一个环,那么该最小环的求法确实是min(g[i][j] + g[i][k] + g[k][j]),所以在此基础上进行修改,只要让i,j,k可以确定一个环即可。可以得到,如果i与k,j与k是直接相连的,即g[i][k] / g[j][k] 路径上仅有一条边,那么i,j,k就可以确定一个环。所以我们可以建立两个数组,一个存储原图——g数组,一个存储最短路径——d数组。
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (d[i][j] + g[j][k] + g[k][i] < res) {
res = d[i][j] + g[j][k] + g[k][j];
cnt = 0;
path[cnt++] = k;
path[cnt++] = i;
getPath(i, j); //求以ij经过的路径
path[cht++] = j;
}
基于此,我们也可以在Floyd算法上进行修改,减少一些时间复杂度。
要求得图上的最小环, 首先要不遗漏的遍历到所有的环, 而为了减少冗余的重复计算, 可以对要求的情况进行一个分类. 以环中编号最大的节点为依据进行分类,第k类表示以k为最大编号的环,而后得到另外两个节点i,j,使g[i][k] / g[j][k]路径仅含一条边,进而得到最小环为min(g[i][j] + g[i][k] + g[k][j])。我们发现Floyd算法的性质,在if(g[i][j] > g[i][k] + g[k][j])的松弛操作中,i,j的最短路径中的中间节点总是不大于当前循环中的k,即在前k-1个节点的松弛操作完成之后,第k个节点的松弛操作还未开始时,d[i][j]如果存在有效值,即存在路径时,该路径的最大中间节点一定不超过k,又让i,j小于k,于是就可以达成第k类的分类思想。核心代码见下。
memcpy(d, g, size d);
for (int k = 1; k <= n; k++) {
for (int i = 1; i < k; i++)
for (int j = i + 1; j < k; j++) {
if (res > g[i][k] + g[k][j] + d[i][j]) {
res = g[i][k] + g[k][j] + d[i][j];
cnt = 0;
path[cnt++] = k;
path[cnt++] = i;
getPath(i, j); //求以ij经过的路径
path[cht++] = j;
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
}
例题
Sightseeing trip
题面:
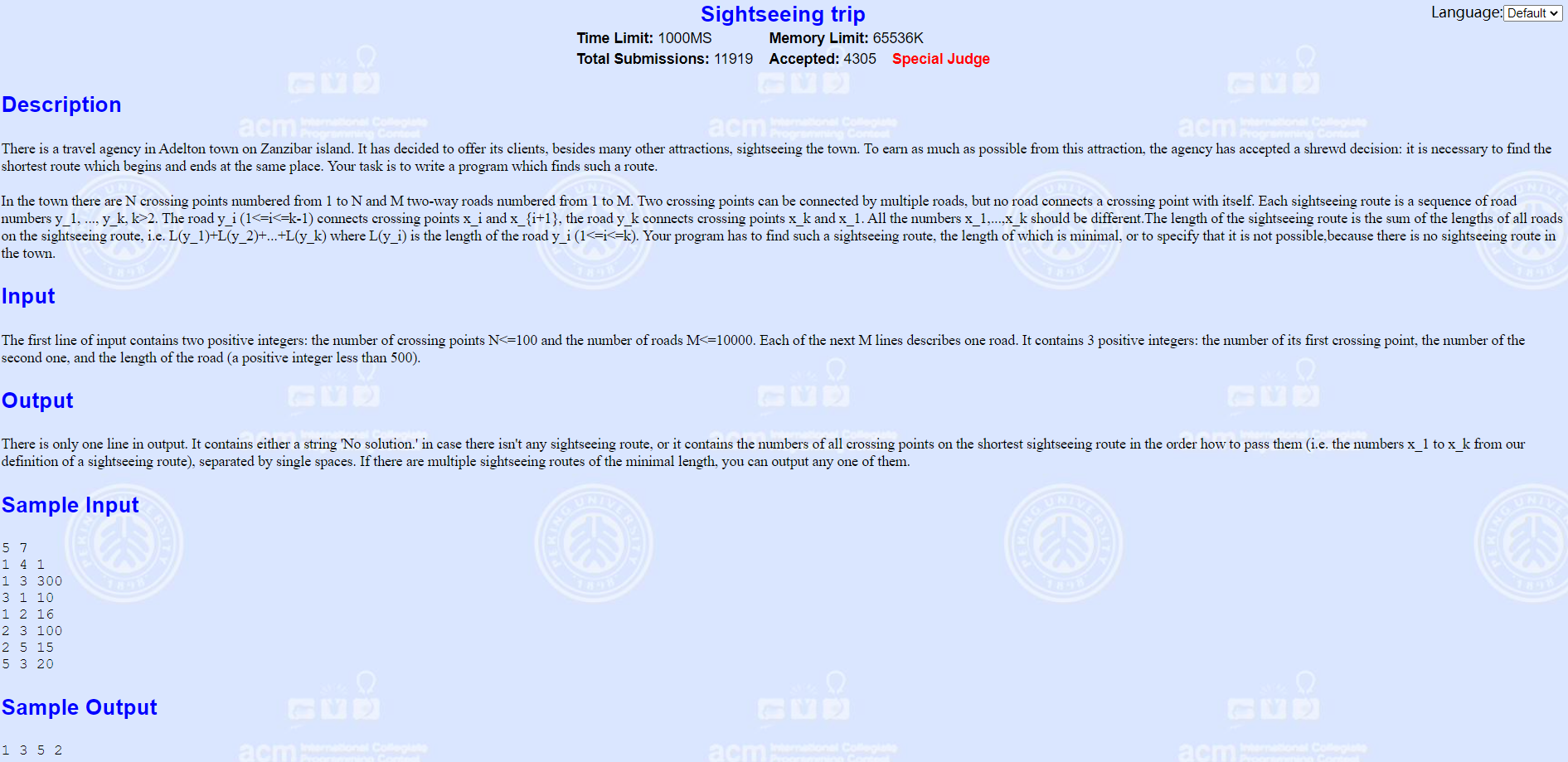
分析:
非常模板的最小环问题,直接求解就行。
动态规划思想
Floyd算法是基于dp得到的,其中第k个节点的思想很值得我们的借鉴,至于更多的关于图论动态规划的思想,在算法专题——最短路已经提到过,这里就不重复提及了,下面直接来看一道题。
例题
Cow Relays
题面:
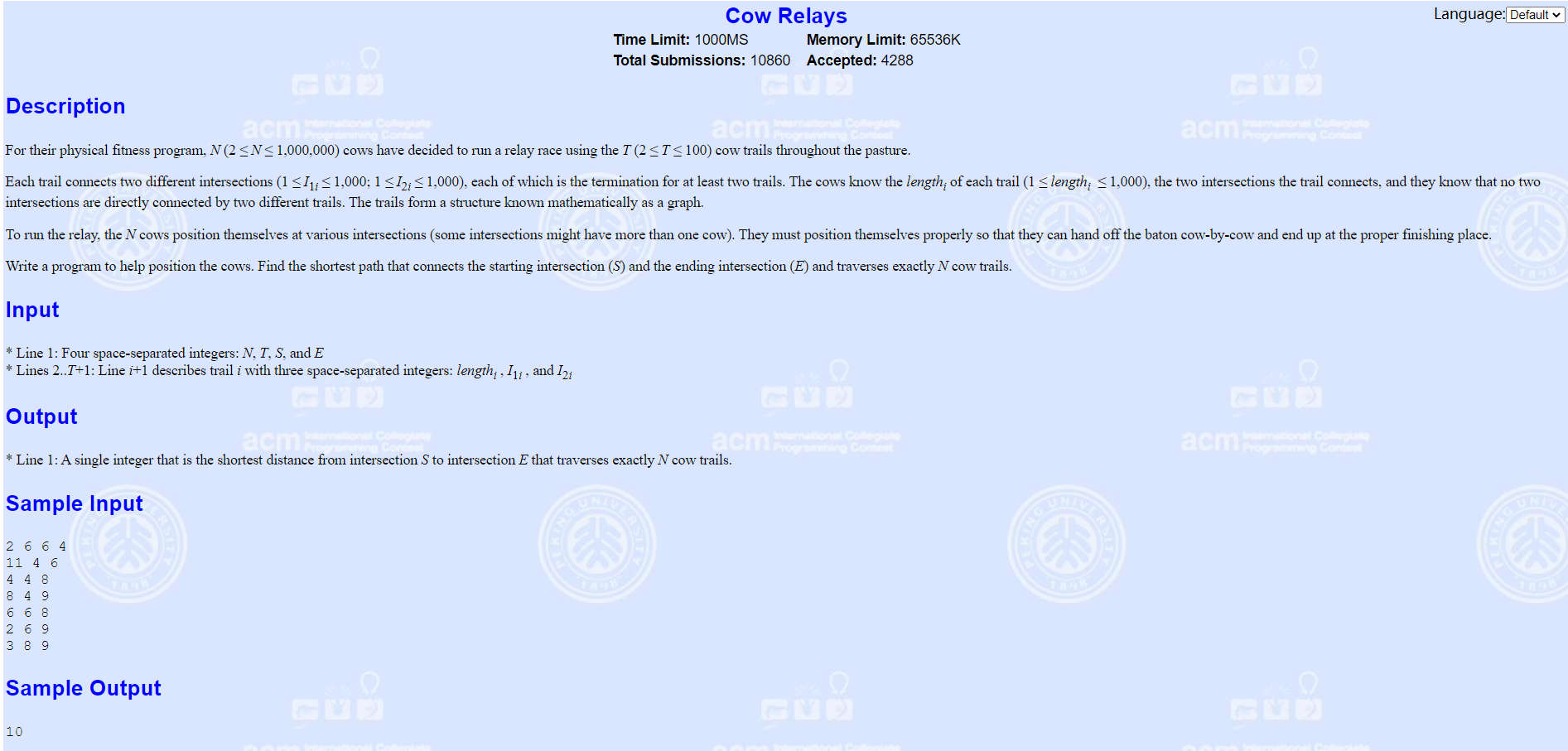
分析:
题意找到一条从起点到达终点且刚好经过N个点的最短路径。
加上了刚好经过N个点的限制之后,这与我们常见的最短路模型都对不上。但是不要紧,结合很多最短路的思想,我们可以考虑将这个限制条件作为信息存储数组中,进而继续思考如何求解刚好经过N个点的最短路。直接口胡一句,这种将信息存储在数组中的方法可以看作动态规划算法的一种,Floyd算法也同样体现了这一点。在下面的分析中,我们也更加贴近于将其作为一道动态规划问题来处理,而不是最短路问题。
首先确定数组状态。根据题目所要求出的东西,可以使用\(dp[num][from][to]\)存储起点为\(from\)点终点为\(to\)点且刚好经过\(num\)个点的最短路径的花费。最终的答案即为\(dp[N][S][E]\)。
很容易得到状态转移方程为:
for(mid : 所有可以到达v的点)
dp[k][u][v] = min(dp[k - 1][u][mid] + mid到v的道路花费)
很容易得到完整的表达式:
for (int k = 2; k <= N; k++)
for (int i = 1; i <= tol; i++)
for (int j = 1; j <= tol; j++)
for (int mid = 1; mid <= tol; mid++)
dp[k][i][j] = min(dp[k - 1][i][mid] + gra[mid][j], dp[k][i][j]);
时间复杂度大概是\(O(NT^3)\),直接炸了。从题目数据可以看到,主要是卡在N这里,需要进行一定的优化。
观察可以发现,设\(dp[k][...][...]\)为记录了所有刚好经过k个点的最短路径,对应为一个二维矩阵。用上述代码得到,\(dp[k][...][...]\)是由\(dp[k-1][...][...]\)得到的。
可以抽象的将由\(dp[k-1][...][...]\)得到\(dp[k][...][...]\)的这一过程抽象为加法(实际上也确实对应矩阵的加法)。
伪代码为:
void Add(int k) {
for (int i = 1; i <= tol; i++)
for (int j = 1; j <= tol; j++)
for (int mid = 1; mid <= tol; mid++)
dp[k][i][j] = min(dp[k - 1][i][mid] + gra[mid][j], dp[k][i][j]);
}
...
for (int k = 2; k <= N; k++)
Add(k);
即得到\(dp[k][...][...] = dp[k-1][...][...]+dp[1][...][...]\),这个表达式在实际意义上也十分形象,即刚好经过\(k\)个点的最短路应该是由刚好经过\(k-1\)个点的最短路在加上一段道路(可以表示为\(dp[1][...][...]\))得到的。
整个的处理过程就是:\(dp[k][...][...] = dp[1][...][...]+...+dp[1][...][...],共k个dp[1][...][...]\)。当我们观察到\(dp[k][...][...]\)具有这一表达形式时,可以很自然的想到快速幂优化(如果接触过的话)。
来讲一下为什么可以用快速幂。原本是要求k个1相加,时间复杂度为线性,但是如果用二进制来表示k,以17为例,得到\((10001)_2\),可以发现\((1)_2\)可以通过\((1)_2+(1)_2\)的方法O(1)得到\((10)_2\),而\((10)_2+(10)_2\)可以O(1)得到\((100)_2\),进而得到可以以\(O(logk)\)实现\(k\)个1的相加。这也是快速幂和慢速乘的原理。
所以效仿快速幂的一般形式,将N分解为二进制处理,得到伪代码。
void q_pow(int dest[][], int a[][], int b[][]); //实现dest[...][...] = a[...][...] + b[...][...],时间复杂度为O(T^3)
...
while (N) {
if (N & 1)
Add(ans, ans, gra);
N >>= 1;
Add(gra, gra, gra);
}
print(ans[S][E]);
时间复杂度为\(O(T^3logN)\)
以上就是通过类Floyd+矩阵快速幂优化时间复杂度解决了这道题。
完整代码:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 300;
int N, M, S, E;
int gra[MAXN][MAXN], ans[MAXN][MAXN], tmp[MAXN][MAXN], mymap[1010], tol;
void q_pow(int dest[][300], int a[][300], int b[][300]) {
memset(tmp, 0x3f, sizeof tmp);
for (int k = 1; k <= tol; k++)
for (int i = 1; i <= tol; i++)
for (int j = 1; j <= tol; j++)
tmp[i][j] = min(a[i][k] + b[k][j], tmp[i][j]);
memcpy(dest, tmp, sizeof tmp);
}
void init() {
scanf("%d%d%d%d", &N, &M, &S, &E);
memset(gra, 0x3f, sizeof gra);
for (int i = 0, u, v, w; i < M; i++) {
scanf("%d%d%d", &w, &u, &v);
if (!mymap[u]) mymap[u] = ++tol;
if (!mymap[v]) mymap[v] = ++tol;
gra[mymap[u]][mymap[v]] = min(gra[mymap[u]][mymap[v]], w);
gra[mymap[v]][mymap[u]] = gra[mymap[u]][mymap[v]];
}
}
int main() {
init();
memset(ans, 0x3f, sizeof ans);
for (int i = 1; i <= tol; i++) ans[i][i] = 0;
while (N) {
if (N & 1)
q_pow(ans, ans, gra);
N >>= 1;
q_pow(gra, gra, gra);
}
printf("%d\n", ans[mymap[S]][mymap[E]]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号