WSS Process On Causal LTI System
Consider a real LTI system with a WSS process $x(t)$ as input and WSS process $y(t)$ as output. Base on the WSS correlation properties,we get these equations
$\begin{align*}
&Time-Domain &:&R_{yy}(\tau) &= h(\tau)*h(-\tau)*R_{xx}(\tau)\\
&Frequency-Domain &:&S_{yy}(j\omega) &= H(j\omega)H^*(j\omega)S_{xx}(j\omega)
\end{align*}$
The way we get $x(t)$ from white noise is no different. Let the input be a white noise with PSD $W_{xx}(j\omega)=1$,which means that its auto-correlation is $\delta$. Then the system can be seen to be a modeling filter denoted by $m(t)$ in time-domain and $M_{xx}(j\omega)$ in frequency-domain.
This can be summarized as the following equations
$\begin{align*}
&Time-Domain &:&R_{xx}(\tau) &= m_{xx}(\tau)*m_{xx}(-\tau)\\
&Frequency-Domain &:&S_{xx}(j\omega) &= M_{xx}(j\omega)M_{xx}^*(j\omega)
\end{align*}$
Now, to think of a system which is the cascade of the filter $m_{xx}(\tau)$ and $m_{xx}(-\tau)$.
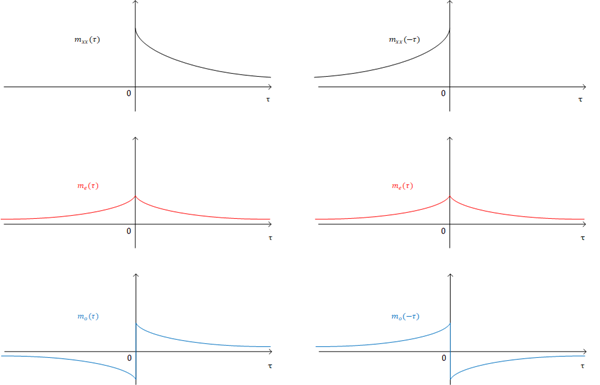
The filter $m_{xx}(\tau)$ can be decomposed into the sum of an even part $m_e(\tau)$, and an odd part $m_o(\tau)$
$m_{xx}(\tau) = m_e(\tau)+m_o(\tau)$
where
$\begin{align*}
m_e(\tau)&= \frac{1}{2}(m_{xx}(\tau)+m_{xx}(-\tau))\\
m_o(\tau)&= \frac{1}{2}(m_{xx}(\tau)-m_{xx}(-\tau))\\
\end{align*}$
If the filter $m_{xx}(\tau)$ is causal, in order that $m_{xx}(\tau)=0$ for $\tau<0$, we require that
$m_o(\tau) = \left\{\begin{matrix}
m_e(\tau), &\tau >0 \\
-m_e(\tau), &\tau<0
\end{matrix}\right.\ =sgn(\tau)m_e(\tau)$
Then the causal impulse response may be written in terms of the even function alone
$\begin{align*}
&m_{xx}(\tau) &= m_e(\tau)+sgn(\tau)m_e(\tau)\\
&m_{xx}(-\tau) &= m_e(\tau)-sgn(\tau)m_e(\tau)
\end{align*}$
For example
In the frequency domain, the frequency response function $M_{xx}(j\omega)$ can also be expressed in terms of the even function alone
$\begin{align*}
M_{xx}(j\omega) &= \mathcal{F}\Big\{m_e(\tau)\Big\}+\mathcal{F}\Big\{sgn(\tau)m_e(\tau)\Big\}\\
&= \mathcal{F}\Big\{m_e(\tau)\Big\}+\frac{1}{2\pi}\mathcal{F}\Big\{sgn(\tau)\Big\}\otimes \mathcal{F}\Big\{m_e(\tau)\Big\}\qquad convolution\ theorem\\
&= M_e(j\omega) + j\left[\frac{1}{\pi\omega}\otimes M_e(j\omega) \right]\\
&= M_e(j\omega) + j\widehat{M}_e(j\omega) \qquad \widehat{M}_e(j\omega)\ means\ Hilbert\ Transform\ of\ M_e(j\omega)
\end{align*}$
The frequency response function $M_{xx}^*(j\omega)$ can be derived with the same argument.
$\displaystyle{M_{xx}^*(j\omega) = M_e(j\omega) - j\widehat{M}_e(j\omega)}$
Thus
$\begin{align*}
S_{xx}(j\omega)&=M_{xx}(j\omega)M_{xx}^*(j\omega)\\
&=\Big\{M_e(j\omega)+j\widehat{M}_e(j\omega)\Big\}\Big\{M_e(j\omega)-j\widehat{M}_e(j\omega)\Big\}\\
&=M_e^2(j\omega)+\widehat{M}_e^2(j\omega)
\end{align*}$
Back to the WSS process, $S_{xx}(j\omega)$ is the PSD of $x(t)$. For real WSS process, the PSD should meet 3 condictions:even, real, non-negative. These condictions can be easily varified on $M_e^2(j\omega)+\widehat{M}_e^2(j\omega)$.
- $M_e^2(j\omega)+\widehat{M}_e^2(j\omega)$ is real, because it is the sum of square
- $M_e^2(j\omega)+\widehat{M}_e^2(j\omega)$ is non-negative, because it is the sum of square
- The first term is the square of FT of real even function, so that $M_e(j\omega)$ is real and even. The second term is the Hilbert transform of the real even function $M_e(j\omega)$. According to the Hilbert transform duality, $\widehat{M}_e(j\omega)$ is odd, which means that $\widehat{M}_e^2(j\omega)$ is even. With these understanding, it is evident that $M_e^2(j\omega)+\widehat{M}_e^2(j\omega)$ is even.
Reference :
Alan V. Oppenheim: Signals, Systems and Inference, Chapter 11: Wiener Filtering

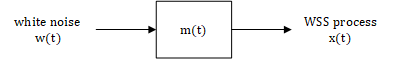


 浙公网安备 33010602011771号
浙公网安备 33010602011771号