概率模型
本文讨论的是信号处理中用到的概率模型(Probabilistic Models),主要目的是为了了解概率模型相关的基础概念,以供后续文章展开更为深入的讨论。
符号定义
首先规定概率模型所采用的符号。概率模型所设计的基础符号分为三个部分:
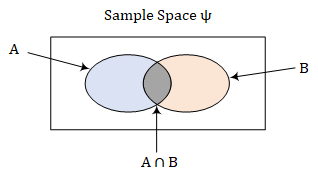
1. Sample Space 样本空间,也就是一个概率模型的总空间,用$\Psi$表示,采样空间内包含了所有可能的outcome(输出)$\psi$。每一次experiment(实验)能产生一个输出
2. Event Algebra 事件代数,通常简称为event(事件),表示的是采样空间内某些输出的集合。如果在实验中产生的一个输出属于某个事件,我们可以理解为发生了该事件。按照这种说法,$\Psi$是一个必然事件,$\varnothing$是一个不可能事件。
3. Probability Measure 概率测度。对于事件A,其概率为$P(A)$。
(a) $P(A)\geq 0$
(b) $P(\Psi) = 1$
(c) $A\cap B =\varnothing \Leftrightarrow P(A\cup B)=P(A)+P(B)$
画图能使得概率模型更容易理解
贝叶斯规则Bayes'Rule
贝叶斯公式
有事件A与B,两者的概率分别为$P(A)$与$P(B)$,它们在样本空间有如下表示
在事件B已发生的情况下,事件A出现的概率记为$P(A|B)$。对照上方的样本空间,可以发现事件$P(A|B)$就是事件$A\cap B$占事件B的比率。
$P(A|B) \triangleq \frac{P(A\cap B)}{P(B)}, \qquad P(B)\neq 0$
反过来有:
$P(A\cap B) = P(A|B)P(B)$
同理也能得到
$P(A\cap B) = P(B|A)P(A)$
把上面两个式子组合起来就能得到贝叶斯的一个公式
$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$
独立事件
如果事件A与B的概率满足以下条件,我们就认为两者相互独立
$P(A|B) = P(A)\qquad or\qquad P(A\cap B) = P(A)P(B)$
即事件A在整个样本空间内的概率为$P(A)$,事件A在样本空间$B$内的概率仍然是$P(A)$。
随机变量Random Variables
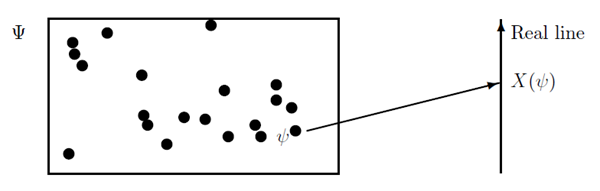
由于输出$\psi$只是集合$\Psi$中的元素,为了方便进行数学上的分析,我们需要把$\psi$映射到实数$X(\psi)$,该实数被称为随机变量,通常称为随机变量$X$,请注意这是一个变量。
Outcome(输出)有可能是离散的,如抛一次硬币只能是正面或者反面;也有可能是连续的,如在记录某时刻的温度时,温度可以是某个温度区间内的任何值。因此有以下随机变量
离散随机变量(Discrete Random Variable)
$X=\left\{\begin{matrix}1, & heads\\ 0, & tails \end{matrix} \right.$
连续随机变量(Continuous Random Variable)
$X={the\ exact\ temprature\ detected\ at\ 12:00\ am}$
上面分别是离散以及连续输出到随机变量X的映射,X表示的是一个可能的取值,如上面的离散的情况取值可能为0或者1,而连续的情况取值则可能为区间上的任意一个值。
概率的相关函数
累计分布函数Cumulative Distribution Functions
累计分布函数(CDF)的输出是从$-\infty$到变量$x$的累计概率
$F_X(x) = P(X\leq x)$
因此有
$P(a<X\leq b) = F_X(b) – F_X(a)$
CDF在负无穷端的值为$F_X(-\infty) = 0$,在正无穷端的值为$F_X(\infty) = 1$。
如上图是CDF的一个例子。在点$x_1$处的概率为$P(X=x_1) = F_X(x_1)-F_X(x_1-)$,由此可见上图中$P(X=0)=1$。
结合贝叶斯公式,有
$F_{X|L}(x|L_i) = P(X\leq x|L=L_i) = \frac{P(X\leq x, L=L_i)}{P(L=L_i)}$
$F_{X|L}(x|L_i)$表示的是已知$L=L_i$的情况下的CDF。
概率密度函数Probability Density Functions
对CDF求导就可以得到概率密度函数PDF。
$f_X(x) = \frac{dF_X(x)}{dx}$
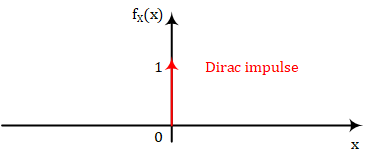
PDF不可能输出负值,因为CDF是一个非递减的函数。如果CDF像上图一样非连续,那么PDF在非连续点处的值就是一个脉冲(Dirac impulse)。
按照PDF的定义,有
$P(a<X\leq b) =F_X(x)\Big|_a^b = \displaystyle{\int_a^bf_X(x)dx}$
在$x$点处的的概率为
$P(x) = \displaystyle{\int_{x-dx}^{x}f_X(x)dx}\approx f_X(x)dx$
概率质量函数Probability Mass Function
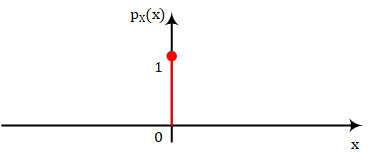
如果概率模型的随机变量$X$是离散的,该概率模型的PDF将会如上图一样,只会在特定的值上出现脉冲,其余的值为0。这种情况用PMF就能表示,PMF是一个离散函数,只需要记录某点上的概率
$pX(x_j) = P(X=x_j)$
上面的例子用PMF来表示如下图
联合分布随机变量Jointly Distributed Random Variables
定义
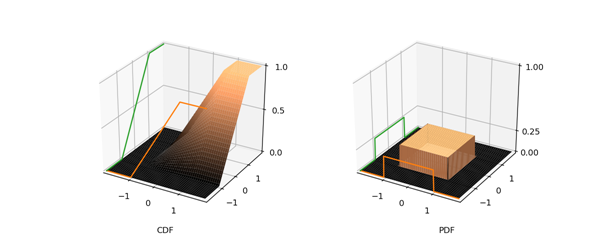
概率模型通常都有多个随机变量,如下是有两个随机变量X与Y的概率模型的CDF
$F_{X,Y}(x,y) = P(X\leq x, Y\leq y)$
对应的PDF为
$f_{X,Y}(x, y) = \frac{\partial^2 F_{X,Y}(x,y) }{\partial x\partial y}$
单边PDF $f_X(x)$的定义就是随机变量$X$的PDF,它跟联合密度函数$f_{X,Y}(x,y)$之间的关系是
$f_X(x) = \displaystyle{\int_{-\infty}^{\infty}f_{X,Y}(x,y)dy}$
同样,$f_Y(y)$也有这种关系。
概率表达
在点$(x,y)$上的概率为
$P(x, y) \approx f_{X,Y}(x,y)dxdy$
贝叶斯规则
在已知$Y=y$(事件B)的情况下,发生$X=x$(事件A)的概率为
$P(A|B) = P(X=x|Y=y)=F_{X|Y}(X=x|Y=y) $
同时又有
$P(A|B) = \frac{P(A\cap B)}{P(B)}=\frac{P(X=x, Y=y)}{P(Y=y)}=\frac{f_{X,Y}(x,y)dxdy}{f_Y(y)dy}$
如果我们假设随机变量$Y$已经确定$Y=y$,那么$P(X|Y=y)=F_{X|Y}(X|Y=y)$就是一个关于随机变量$X$的函数,该函数对$x$求导得到的是:已知$Y=y$的情况下,随机变量X的概率密度函数$f_{X|Y}(X|Y=y)$,有下面的式子
$f_{X|Y}(x|y) = \frac{dF_{X|Y}(X=x,Y=y)}{dx}=\frac{f_{X,Y}(x,y)dxdy}{f_Y(y)dydx} = \frac{f_{X,Y}(x,y)}{f_Y(y)}$
进一步推导还能得到
$\begin{align*}
P(B|A)
&= \frac{f_{X,Y}(x,y)dxdy}{f_X(x)dx}\\
&=\frac{f_{X,Y}(x,y)dy}{f_X(x)}\\
&=\frac{f_{X|Y}(x|y) f_Y(y)dy}{f_X(x)}\\
&=\frac{f_{X|Y}(x|y)P(Y=y)}{f_X(x)}\\
&=\frac{f_{X|Y}(x|y)P(B)}{f_X(x)}
\end{align*}$
独立事件
如果包含随机变量$X$与$Y$的联合分布的CDF或者PDF满足如下条件,则$X$与$Y$所属的事件相互独立
$f_{X,Y}(x,y) = f_X(x)f_Y(y)$
$F_{X,Y}(x,y) = F_X(x)F_Y(y)$
期望(Expectations)、矩(Moments)以及方差(Variance)
期望
The expectation — also termed the expected or mean or average value, or the first-moment — of the real-valued random variable X is denoted by $E[X]$ or $\overline{X}$ or $\mu_X$, and defined as
$E[X] = \overline{X} = \mu_X = \displaystyle{\int_{\infty}^{\infty}xf_X(x)dx}$
期望具有线性性质
$\begin{align*}E[X+Y] &=\int_{-\infty}^{\infty}xf_{X+Y}(x)dx\\
&=\int_{-\infty}^{\infty}x\Big(f_X(x)+f_Y(x)\Big)dx\\
&=\int_{-\infty}^{\infty}xf_X(x)dx+\int_{-\infty}^{\infty}xf_Y(x)dx\\
&=E[X]+E[Y]
\end{align*}$
方差
The variance or centered second-moment of the random variable $X$ is denoted by $\sigma^2$ and defined as
$\begin{align*}\sigma^2 &=E[(X-\mu_X)^2]\\
&= E[X^2-2X\mu_X+\mu_X^2]\\
&= E[X^2]-2\mu_XE[X]+\mu_X^2\\
&= E[X^2]-2\mu_X^2+\mu_X^2\\
&= E[X^2]-\mu_X^2
\end{align*}$
We refer to $E[X2]$ as the second-moment of $X$.
贝叶斯规则
我们这里主要是为了推导得到一条公式
$\color{red}{E[X] = E_{Y}[E_{X|Y}[X|Y]]}$
其中$E_{X|Y}[X|Y]$,即$E[X|Y]$表示是已知随机变量$Y$所代表的事件发生的情况下,随机变量$X$的期望值。按照期望的定义有如下公式
$\begin{align*}
E[X|Y] &= \int_{-\infty}^{\infty}xf_{X|Y}(x|y)dx\\
&=\int_{-\infty}^{\infty}x\frac{f_{X,Y}(x,y)}{f_Y(y)}dx\\
&=g(y)
\end{align*}$
因此$E[X|Y]$是一个以$y$为变量的函数,我们可以认为是:在$Y=y$的前提下,随机变量$X$的期望值是与$y$有关的。
证明:
$\begin{align*}
E_{Y}[E_{X|Y}[X|Y]] &=\int_{-\infty}^{\infty}g(y)f_Y(y)dy\\
&= \int_{-\infty}^{\infty}\left\{\int_{-\infty}^{\infty}xf_{X|Y}(x|y)dx\right\}f_Y(y)dy\\
&=\int_{-\infty}^{\infty}\left\{\int_{-\infty}^{\infty}x\frac{f_{X,Y}(x,y)}{f_Y(y)}dx\right\}f_Y(y)dy\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X,Y}(x,y)dxdy\\
&=\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}f_{X,Y}(x,y)dydx\\
&=\int_{-\infty}^{\infty}xf_X(x)dx\\
&=E[X]
\end{align*}$
这说明我们在不知道$f_X(x)$的情况下,通过$f_Y(y)$以及$g(y)$就能得到随机变量$X$的期望值。
独立事件
有两个随机变量分别为$Y,Z$,令$X=h(Y,Z)$,那么$X$也是一个随机变量,其期望为$E[X]$。现假设$h(y,z) = g(y)\ell(z)$,并且$Y$与$Z$相互独立,因此有
$\begin{align*}
E[X]&= E[g(y)\ell(z)] \\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(y)\ell(z)f_{Y,Z}(y,z)dydz\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(y)\ell(z)f_{Y}(y)f_{Z}(z)dydz\\
&=\int_{-\infty}^{\infty}g(y)f_Y(y)dy\int_{-\infty}^{\infty}\ell(z)f_Z(z)dz\\
&=E[g(y)]E[\ell(z)]
\end{align*}$
相关性与协方差 correlation and covariance
在对随机变量进行处理时,很多情况下都无法知道该随机变量的PDF,此时我们只能通过expectation以及variance对随机变量进行描述,expectation代表的是随机变量的location,即随机变量的中心点;variance代表的是随机变量的spread,即随机变量的扩散程度。这两个值我们能通过对随机变量的反复实验然后求得。
而对于联合分布的随机变量$(X,Y)$,我们能得到其location为$(E[X],E[Y])$,不过spread就比较难表达了,因为$\sigma_X$以及$\sigma_Y$都只是单个随机变量的方差,而$X$与$Y$之间也有可能存在某种相关关系,因此联合分布的spread不应该把随机变量分开进行单独讨论。
联合随机变量的location与spread
为了表达联合分布的spread,下面我们假设有一个随机变量$Z$,有
$Z=\alpha X + \beta Y$
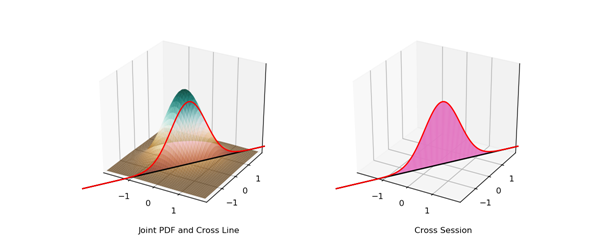
其中$\alpha$与$\beta$分别为随机变量$X$与$Y$的系数,可以选任意常数。上面关于随机变量$Z$的式子也能看作是一条关于$X$与$Y$的直线,当选取固定的$Z$后,在$X,Y$平面上就能得到一条直线,而通过改变$Z$就能覆盖整个$X,Y$平面。
经过该直线并垂直于XY平面的平面与联合PDF曲面相交所得的曲线,展示的就是当$Z$取某个固定值时,随机变量$X$与$Y$的取值的概率。对该曲线进行积分能得到$Z$取该固定值的概率。比如说
$P_Z(z=0) = \displaystyle{\int_{\alpha x+\beta y=0}f_{X,Y}(x,y)dxdy}$
不过这并不是我们要讨论的重点。
对于随机变量$Z$,有expectation为
$E[Z] = E[\alpha X + \beta Y] = \alpha E[X] + \beta E[Y]$
有variance为
$\begin{align*}
\sigma_Z^2 &= E[(Z-E[Z])^2]\\
&=E[Z^2-2E[Z]Z+(E[Z])^2]\\
&=E[Z^2]-2(E[Z])^2+(E[Z])^2\\
&=E[Z^2]-(E[Z])^2\\
&=E[(\alpha X+\beta Y)^2]-(\alpha E[X]+\beta E[Y])^2\\
&=E[\alpha^2X^2+2\alpha\beta XY+\beta^2Y^2]-\Big\{\alpha^2(E[X])^2+\beta^2(E[Y])^2+2\alpha\beta E[X]E[Y]\Big\}\\
&=\alpha^2 E[X^2]+2\alpha\beta E[XY]+\beta^2E[Y^2]-\alpha^2(E[X])^2-2\alpha\beta E[x]E[Y]-\beta^2(E[Y])^2\\
&=\alpha^2\Big\{E[X^2]-(E[X])^2\Big\}+\beta^2\Big\{E[Y^2]-(E[Y])^2\Big\}+2\alpha\beta\Big\{E[XY]-E[X]E[Y]\Big\}\\
&=\alpha^2\Big\{E[(X-E[X])^2]\Big\}+\beta^2\Big\{E[(Y-E[Y])^2]\Big\}+2\alpha\beta\Big\{E[(X-E[X])(Y-E[Y])]\Big\}\\
&=\alpha^2\sigma_X^2+\beta^2\sigma_Y^2+2\alpha\beta\sigma_{X,Y} \qquad letting\ \sigma_{X,Y}=E[(X-E[X])(Y-E[Y])]
\end{align*}$
其中$\sigma_{X,Y}$被称为covariance,记为$C_{X,Y}$或者$cov(X,Y)$有
$\color{red}{\sigma_{X,Y} =C_{X,Y}= E[(X-E[X])(Y-E[Y])] = E[XY]-E[X]E[Y]}$
$E[XY]$被称为correlation,记为$R_{X,Y}$。
$\color{red}{R_{X,Y} = E[XY]}$
根据前面的推导,只要我们知道$\sigma_X^2,\sigma_Y^2,\sigma_{X,Y}$的值,就能得到联合随机变量的spread。这其中只有$\sigma_{X,Y}$是新出现的概念。另外,从前面的推导中我们又能得知$\sigma_{X,Y}$可以通过$R_{X,Y}$计算得到。
相关系数correlation coefficient $\rho$
$\rho$的定义
前面已经得到随机变量$Z$的variance为
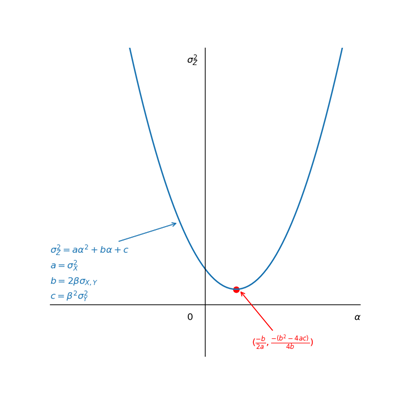
$\sigma_Z^2 = \alpha^2\sigma_X^2+\beta^2\sigma_Y^2+2\alpha\beta\sigma_{X,Y}$
我们这里把$\sigma_Z^2$作为纵轴,$\alpha$作为横轴,其余参数当成常量,得到一个一元二次方程。
由于variance必定大于0,因此有
$\frac{-(b^2-4ac)}{4a}=\frac{-[(2\beta\sigma_{X,Y})^2-4\sigma_X^2 \beta^2\sigma_Y^2]}{4\beta^2\sigma_X^2}=\frac{\beta^2\sigma_X^2\sigma_Y^2-\beta^2\sigma_{X,Y}^2}{\sigma_X^2}\geq 0$
整理可得到
$\color{red}{|\rho| = \left|\frac{\sigma_{X,Y}}{\sigma_X \sigma_Y}\right|\leq 1}$
$\rho$就是correlation coefficient,虽然我们把它叫做correlation coefficient,不过从上面的式子看来,$\rho$跟covariance的关系更密切。
$\rho$其实就相当于对covariance进行了标准化。
随机变量标准化后的随机变量的expectation为0,variance为1,即
$V = \frac{X-\mu_X}{\sigma_X},\qquad W = \frac{Y=\mu_X}{\sigma_Y}$
expectation以及variance的变化如下
$E[V] = E\left[\frac{X-\mu_X}{\sigma_X}\right] = \frac{E[X]-\mu_X}{\sigma_X}=0$
$\sigma_V^2=E[(V-E[V])^2]=E[V^2]=E\left[\frac{(X-\mu_X)^2}{\sigma_X^2}\right]=E\left[\frac{\sigma_X^2}{\sigma_X^2} \right ]=1$
correlation coefficient的变化如下
$\begin{align*}\sigma_{V,W}&=E[VW]-E[V]E[W]=E[VW]\\
&=E\left[\frac{X-\mu_X}{\sigma_X}\cdot\frac{Y-\mu_Y}{\sigma_Y}\right]\\
&=E\left[\frac{XY-X\mu_Y-Y\mu_X+\mu_X\mu_Y}{\sigma_X\sigma_Y}\right]\\
&=\frac{E[XY]-E[X]E[Y]}{\sigma_X\sigma_Y}\\
&=\frac{\sigma_{X,Y}}{\sigma_X\sigma_Y}\end{align*}$
这也证明了即使随机变量加上或者乘以一个常数,这并不会改变其correlation coefficient。
$\rho$的实际意义
我们容易知道correlation的值$E[XY]$如果大于0,则表明$X$与$Y$倾向于有相同的符号;如果correlation的值小于0,则表明$X$与$Y$倾向于有相反的符号。那么对于$\sigma_{X,Y} = E[(X-\mu_X)(Y-\mu_Y)]$,如果大于0,则表明$X-\mu_X$与$Y-\mu_Y$倾向于有相同的符号,当$X=Y$时,$\sigma_{X,X}=\sigma_X^2$,反之亦然。
同理,$\rho$作为covariance的标准化的值
- 如果$\rho>0$则表明$X-\mu_X$与$Y-\mu_Y$倾向于有相同的符号
- 如果$\rho$越接近1,$X$与$Y$之间会有更紧密的关系(正相关)
- 反之,如果$\rho$越接近-1,$X$与$Y$之间的关系趋于相反(负相关)
- 如果$\rho=0$,则有$\sigma_{X,Y}=0$,$E[XY]=E[X]E[Y]$,表明$X$与$Y$相互独立
相关性的向量空间分析
从随机变量到向量空间的转换规则
我们可以把随机变量看作向量,把correlation看作向量的内积,内积用尖括号来表示。因此有
$<\textbf{X}, \textbf{Y}> = E[XY] = R_{X,Y}$
内积满足交换律以及分配律
$<\textbf{X},\textbf{Y}> = <\textbf{Y}, \textbf{X}>$
$<\textbf{X},a_1 \textbf{Y}_1+a_2 \textbf{Y}_2>=a_1<\textbf{X},\textbf{Y}_1>+a_2<\textbf{X},\textbf{Y}_2>$
如果两个向量正交,那么他们的内积为0
$<\textbf{X},\textbf{Y}>=E[XY]=0$
向量的长度,也就是向量的模为
$\left\|\textbf{X}\right\|=\sqrt{<\textbf{X},\textbf{X}>}=\sqrt{E[X^2]}$
实用的向量空间
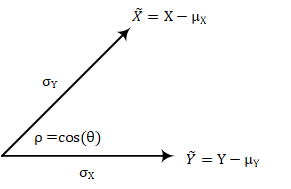
下面我们令向量$\widetilde{\textbf{X}}$以及$\widetilde{\textbf{Y}}$分别为
$\widetilde{\textbf{X}}=X-\mu_X ,\qquad \widetilde{\textbf{Y}}=Y-\mu_Y$
这两个向量的模分别为
$||\widetilde{\textbf{X}}||=\sqrt{E[(X-\mu_X)^2]}=\sigma_X,\qquad ||\widetilde{\textbf{Y}}||=\sqrt{E[(Y-\mu_Y)^2]}=\sigma_Y$
那么这两个向量的内积就是
$<\widetilde{\textbf{X}}, \widetilde{\textbf{Y}}>=E[(X-\mu_X)(Y-\mu_Y)]=\sigma_{X,Y}$
按照向量的定义,内积与模之间有如下关系
$<\widetilde{\textbf{X}},\widetilde{\textbf{Y}}>=||\widetilde{\textbf{X}}|| \cdot||\widetilde{\textbf{Y}}||\cdot cos(\theta)$
即
$\sigma_{X,Y}=\sigma_X \sigma_Y cos(\theta)$
其中$\theta$为向量$\widetilde{\textbf{X}}$与向量$\widetilde{\textbf{Y}}$之间的夹角。根据前面已得到的结论,我们得知$\rho=cos(\theta)$,而又由于$\rho$满足$-1\leq \rho \leq 1$,因此把随机变量推广到向量空间的这种做法正好合适。
在该这里假设的向量空间中,$\omega_{X,Y}=0$表明$\widetilde{\textbf{X}}与向量\widetilde{\textbf{Y}}$正交。
Reference:
Alan V. Oppenheim: Signals, Systems and Inference, Chapter 7: Probabilistic Models



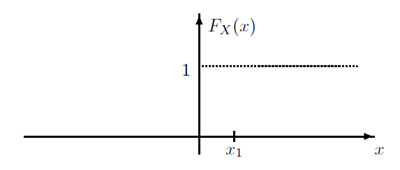

 浙公网安备 33010602011771号
浙公网安备 33010602011771号