P10979 任务安排 2

容易发现这题就是 P2365 的 \(O(n)\) 做法。
先考虑很裸的状态 \(dp_{i,j}\),表示当前考虑到第 \(i\) 位,共分为 \(j\) 批任务的最小代价。显然有转移
发现这个东西很慢,复杂度来到 \(O(n^4)\)。考虑前缀和,能够优化到 \(O(n^3)\)。\(sumT_i=\sum \limits _{j=1} ^{i}T_j\),\(sumC_i=\sum \limits _{j=1} ^{i} C_j\)。下文同。
用一个叫做费用提前计算优化的东西。考虑现有状态 \(dp_{i,j}\) 中,我们拿 \(j\) 只是用来计算 \(s\times j\) 的。如果我们令从 \(l\) 转移到 \(r\) 表示 \(l+1\) 到 \(r\) 内的任务分为一批,那么当前是第几批不重要。此时启动时间 \(s\) 总会对后面的处理增加代价,所以直接加上即可。发现状态的第二维可以被优化。
转移为
其中 \(s\times(sumF_n−sumF_{j-1})\) 为当前分批造成的启动时间对后面所有任务带来的代价。
此时复杂度是 \(O(n^2)\) 的。
我们无法用单调数据结构优化它,原因在于 \(i\) 和 \(j\) 混在一起。也就是说,我们需要对它继续变形。
这里 \(\min\) 本质上在求最小的 \(dp_i\),也就是说找到一个 \(j\) 使得 \(dp_i\) 最小即可。我们把它去掉,并对原式展开,有:
会发现我把 \(i\) 和 \(j\) 分离开了。
不妨记 \(b=dp_i-sumT_i\times sumF_i-s\times sumF_n\),\(x=sumF_{j-1}\),\(k=sumT_i+s\),对原式移项然后带入,变成了一个很美观的东西:
它可以变成我们很喜欢的 \(y=xk+b\),也就是说这个东西就是一个一次函数。
因为 \(sumT_i\times sumF_i-s\times sumF_n\) 是定值,所以最终我们希望 \(b\) 最小。\(dp_i\) 一定需要由某个 \(j\) 转移而来,也就是说,需要有某个 \((x,y)\) 在该直线上。代入 \(x,y\) 得 \((sumF_{j-1},dp_{j-1})\)。然后可以把它们扔到平面直角坐标系上,拿直线从下往上扫,第一个点就是可以更新的 \(j\)。
所以我们将问题转化为:有 \(n\) 个点在平面直角坐标系上,有一条斜率固定的直线,问最小的截距是多少。
我们考虑维护下凸的点集,如果不知道是什么也没有关系,可以看下面这个东西:
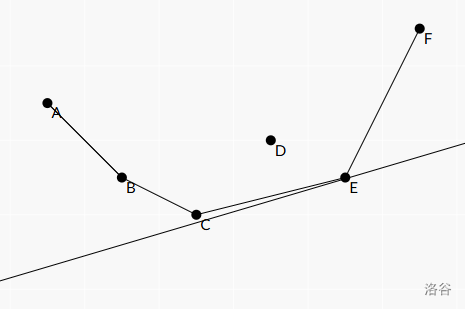
由于技术原因,没能画出 \(x\) 和 \(y\) 轴,就姑且把图片的左下角看作原点吧。
可以大致理解为先下降后上升的一些点(上凸反之)。当我们拿任意一条直线从下往上去“切”这些点时,只有下凸点集上的点可能被“切”到。如上图,不可能切到 \(D\) 点。
考虑如何维护。假设上图按照字母顺序加点,已经加入 \(D\) 点。这个时候所有点都在下凸点集内。此时要加入一个点 \(E\),发现 \(D\) 点不能在下凸点集中,否则不下凸。
也就是说,若 \(CD\) 斜率大于 \(DE\) 斜率,那么 \(D\) 将不会再出现在下凸点集中了。
记 \(C\) 的坐标为 \((C_x,C_y)\),以此类推,那么 \(D\) 将不在点集内仅当 \(\frac{D_y-C_y}{D_x-C_x}\ge \frac{E_y-D_y}{E_x-D_x}\)。事实上三点共线舍去不劣。
这个东西就可以拿单调队列维护了。答案是在单调队列中第一次出现的,斜率大于或等于当前考虑直线的斜率的线段的靠左的端点(好绕啊)。
发现直线 \(y=xk+b\) 的斜率递增,所以可以及时排除掉无法成为答案的线段。
然后把计算斜率的部分叉乘一下,防止挂精度。
inline int read(){
char ch=getchar();
int s=0;
int w=1;
while(ch<'0' or ch>'9'){
if(ch=='-')
w=-1;
ch=getchar();
}
while(ch>='0' and ch<='9'){
s=(s<<3)+(s<<1)+(ch xor 48);
ch=getchar();
}
return s*w;
}//快读自动掠过
int n;
int s;
class node{
public:
int f=0;
int t=0;
inline friend node operator+(node a,node b){
node c;
c.t=a.t+b.t;
c.f=a.f+b.f;
return c;
}
}a[100086],sum[100086];
class Que{
public:
int q[1000086];
int l=1;
int r=0;
inline void pop(){
l++;
return;
}
inline void push(int x){
q[++r]=x;
return;
}
inline void pop_b(){
r--;
return;
}
inline bool empty(){
return l>=r;
}
}q;//手写了一下双端队列
int dp[1000086];
inline bool check(int ax,int ay,int bx,int by,int cx,int cy){
return (by-ay)*(cx-bx)>=(cy-by)*(bx-ax);//交叉相乘
}
#define k (s+sum[i].t)
#define c (sum[i].t*sum[i].f+s*sum[n].f)
signed main(){
n=read();
s=read();
memset(dp,0x7f,sizeof dp);
for(int i=1;i<=n;i++){
a[i].t=read();
a[i].f=read();
sum[i]=a[i]+sum[i-1];//维护前缀和
}
dp[0]=0;
q.push(0);//一定要往里面丢一个0,否则无法更新
for(int i=1;i<=n;i++){
while((not q.empty()) and dp[q.q[q.l+1]]-dp[q.q[q.l]]<=k*(sum[q.q[q.l+1]].f-sum[q.q[q.l]].f))//若线段斜率小于直线的斜率,那么它将永远不会成为答案
q.pop();
dp[i]=dp[q.q[q.l]]-k*sum[q.q[q.l]].f+c;//此时的队首就是可更新的 j
while((not q.empty()) and check(sum[q.q[q.r-1]].f,dp[q.q[q.r-1]],sum[q.q[q.r]].f,dp[q.q[q.r]],sum[i].f,dp[i]))//凸包更新
q.pop_b();
q.push(i);//不要忘记把当前点扔进去
}
std::cout<<dp[n];
return 0;//撒花
}
斜率优化好可爱。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号