扫描线学习笔记

扫描线学习笔记

今天初学了扫描线，发一篇学习笔记巩固一下

扫描线能干什么

1. 计算矩形面积的并
2. 计算矩形周长的并
3. 其他

引入

如下图所示，给定平面直角坐标系内N个矩形，求矩形的面积并，定义面积的并为矩形并集覆盖坐标系的面积和

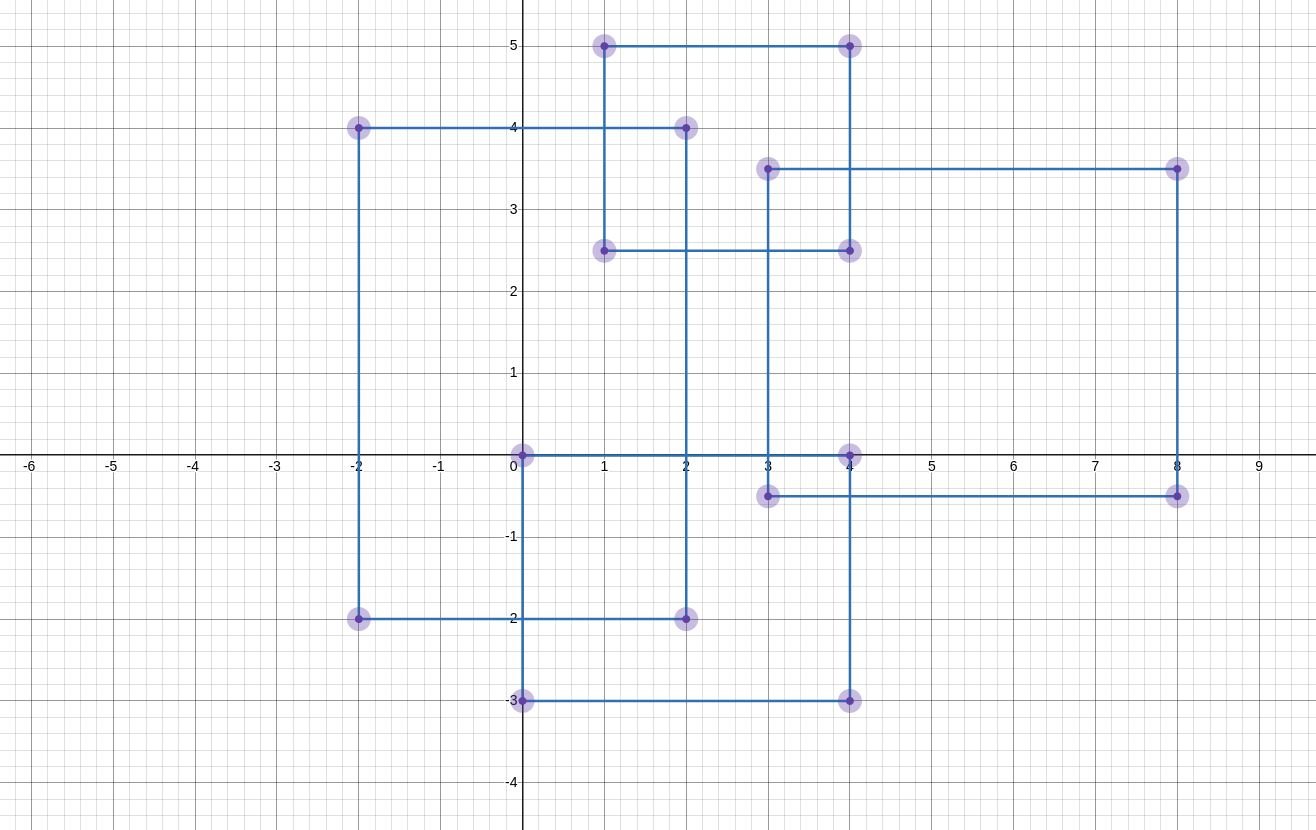
正文部分

面积并：

通过观察，我们发现，对于矩形面积的并，可以通过以每个矩形左右边为分界，分成若干小的规则矩形，所以，我们引入了一种新的思想——扫描线。

顾名思义，这种思想在坐标系内构想了一条从左到右扫描整个坐标系的直线，它在每个矩形的边停顿并更新答案，如下图，红线即为扫描线，这种思想即为扫描线法。

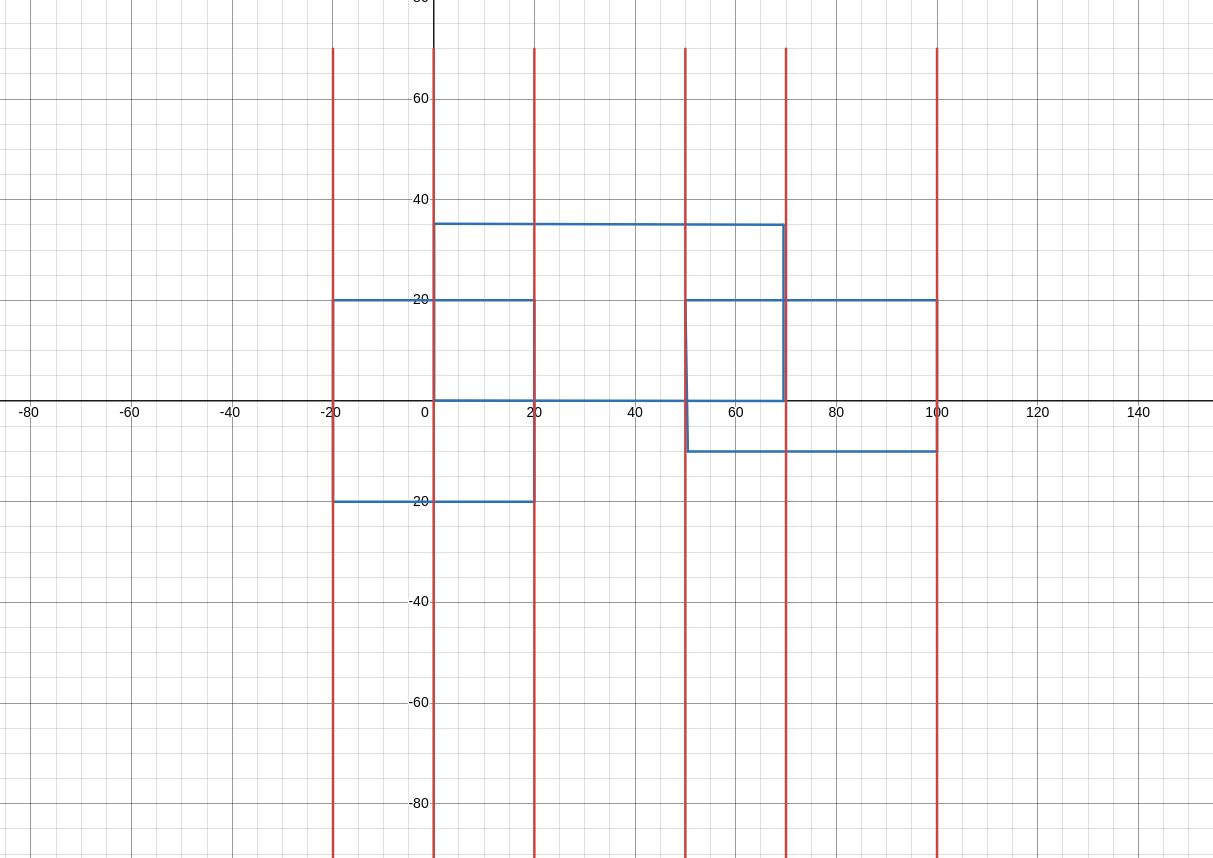
那么我们思考最终答案，根据引入所言，不难注意到，我们在通过扫描线把面积并分成了若干规则图形，通过矩形计算公式即可轻易计算出每部分的答案，具体而言，我们记录每一个扫描线停顿位置的横坐标，定为\(x_1 , x_2 ,x_3 ,x_n\) 对于每一个位置矩形的面积我们可以得出\(S=(x_i-x_{i-1})\times h\)(\(h\)为扫描线此时高度),最后，各扫描线停顿位置之和即为所求。

我们如何维护答案呢，对于每一个停顿位置，我们可以有四元组\((x,y1,y2,d)\)，其中，x为横坐标，\(y1,y2\)为在\(x_i\)处扫描线与整个图形的最低交点和最高交点,对于左边界，\(d=1\)，对于右边界\(d=-1\),如图

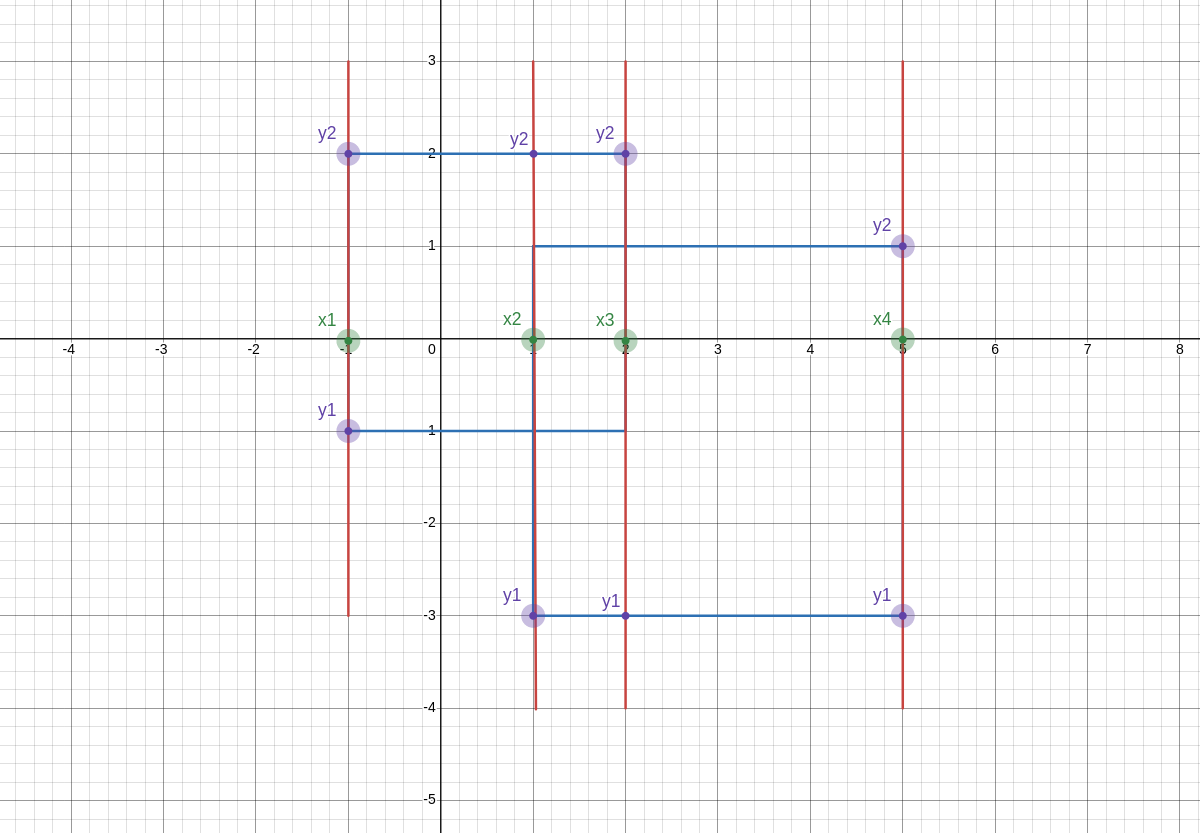
同时，我们给每一个经过纵坐标排序，维护\(raw\)数组，对于\(raw[i]\)，表示从\(y_i\)的坐标，扫描线被每条上下边界分成若干段，对于一段\([y_{i-1},y_i]\)，可以用\(raw\)数组表示。

我们再维护一个数组\(c\)，\(c[i]\)表示到目前位置，第\(i\)个区间段被覆盖的次数，按\(x\)升序遍历四元组，每次给\([y_1,y_2]\)每一段加上\(d\)，\(c[i]>0\)表示这个区间目前仍被覆盖，\(\sum_{c[i]>0}{raw[i]-raw[i-1]}\)即为扫描线到当前节点的\(h\)，统计答案即可，至此我们得到了\(O(n^2)\)做法。

观察上述求解过程，我们在对\(c\)数组做区间修改并访问整个\(raw\)数组区间和，不难想到，我们可以用线段树维护。不同与普通线段树，我们只需要访问树根的值，所以，我们可以省略push_down操作，改为维护两个数组\(len\)和\(cnt\)，\(cnt[i]\)表示对于当前线段树节点的\([l,r]\)被覆盖了几次，\(len[i]\)表示，当前节点\([l,r]\)对于\(h\)的贡献。显然，整体的\(h\)就是根节点的\(len\)，值得注意的是，push_up操作有所不同，如果当前节点的\(cnt>0\),表示当前节点对应的\([l,r]\)被全覆盖，所以再加上子节点的贡献就重复了，此时\(len[i]=raw[r+1]-raw[l]\)，否则，就通过子节点更新。同时，因为更新\(len\)值可能是通过子节点，所以，在该节点被全部包含也就是\(return\)之前，也要push_up。

最后提醒一句，大部分扫描线需要离散化。

线段树部分:

#define lx x<<1
#define rx (x<<1)+1
void build(int tl,int tr,int x)
{
    l[x]=tl,r[x]=tr;
    if(l[x]==r[x]) return;
    int mid=(l[x]+r[x])>>1;
    build(tl,mid,lx);
    build(mid+1,tr,rx);
}

void push_up(int x)
{
    if(cnt[x]>0) len[x]=raw[r[x]+1]-raw[l[x]];
    else len[x]=len[lx]+len[rx];
}

void modify(int dl,int dr,int x,int d)
{
    if(dl<=l[x] && dr>=r[x])
    {
        cnt[x]+=d;
        push_up(x);
        return;
    }
    int mid=(l[x]+r[x])>>1;
    if(dl<=mid) modify(dl,dr,lx,d);
    if(dr>mid) modify(dl,dr,rx,d);
    push_up(x);
}

模板：P5490 【模板】扫描线 & 矩形面积并

周长的并：

定义类比面积并。

我们在维护面积并时用到了扫描线停顿位置的\(h\)，显然，这对于求周长并是很有帮助的。

先给出结论：

将四元组按照\(x\)为第一关键字，\(d\)为第二关键字排序后，有：

\(C=\vert \sum_{i=1}^{n}{h_i-h_{i-1}} \rvert+\vert\sum_{i=1}^{n}{w_i-w_{i-1}}\rvert\)（其中\(h\)为横向扫描的高度，\(w\)为纵向扫描的宽度）

随便画几个矩形，手模一下就可以发现\(\vert h_i-h_{i-1}\rvert\)实际上就是\(h\)增加的长度，每次加上$ \Delta h$最终一定是周长左右长度，横纵分别扫一遍就是整个周长。那为什么还要按照 \(d\) 排序呢？观察发现，如果前一个矩形和后一个矩形的左边和右边重合，实际上前一个矩形的右边是没有全部作为周长的，但是由于$ d=1$ 所以，你的代码会将它误认为没有边覆盖它了，也就是全部作为周长的一部分了。这就需要将这个位置所有覆盖的边全部先加上，然后再去判断是否覆盖（感性理解一下，不懂的可以用desmos画图手玩一下），其他的正常跑两边线段树即可。

模板：P1856 [IOI 1998 / USACO5.5] 矩形周长 Picture

代码：

#include<bits/stdc++.h>
#define lx x<<1
#define rx (x<<1)+1
#define x1 qqq
#define x2 www
#define y1 eee
#define y2 rrr 
using namespace std;
const int N=5e4;
int X[N],Y[N];
struct A
{
    int x1,x2;
    int y1,y2;
}sq[2*N];
struct B
{
    int x;
    int yl,yh;
    int vl;
} line[2*N];
struct C
{
    int y;
    int xf,xb;
    int vl;
} level[N];

int len[8*N],cnt[8*N],l[8*N],r[8*N];
int mx,my,pos;
int n;

void dis()
{
    sort(X+1,X+2*n+1);
    mx=unique(X+1,X+2*n+1)-(X+1);
    sort(Y+1,Y+2*n+1);
    my=unique(Y+1,Y+2*n+1)-(Y+1);
}

int askx(int x)
{
    return lower_bound(X+1,X+mx+1,x)-X;
}

int asky(int x)
{
    return lower_bound(Y+1,Y+my+1,x)-Y;
}

void build(int tl,int tr,int x)
{
    l[x]=tl,r[x]=tr,len[x]=cnt[x]=0;
    if(tl==tr) return;
    int mid=(l[x]+r[x])>>1;
    build(l[x],mid,lx);
    build(mid+1,r[x],rx);
}

void push_up(int x,int k)
{
    if(k==1)
    {
        if(cnt[x]) len[x]=X[r[x]+1]-X[l[x]];
        else len[x]=len[lx]+len[rx];
    }

    if(k==2)
    {
        if(cnt[x]) len[x]=Y[r[x]+1]-Y[l[x]];
        else len[x]=len[lx]+len[rx];
    }
}

void modify(int dl,int dr,int x,int d,int k)
{
    if(dl<=l[x] && dr>=r[x])
    {
        cnt[x]+=d;
        push_up(x,k);
        return;
    }
    int mid=(l[x]+r[x])>>1;
    if(dl<=mid)modify(dl,dr,lx,d,k);
    if(dr>mid) modify(dl,dr,rx,d,k);
    push_up(x,k);
}

bool cmp(B a,B b)
{
    if(a.x==b.x) return a.vl>b.vl;
    return a.x<b.x;
}

bool cnp(C a,C b)
{
    if(a.y==b.y) return a.vl>b.vl;
    return a.y<b.y;
}

int main(){
    // freopen("text.in","r",stdin);
    // freopen("text.out","w",stdout);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        sq[i]=(A){x1,x2,y1,y2};
        X[i]=x1;
        X[i+n]=x2;
        Y[i]=y1;
        Y[i+n]=y2;
    }

    dis();
    for(int i=1;i<=n;i++)
    {
        int x1=sq[i].x1,x2=sq[i].x2,y1=sq[i].y1,y2=sq[i].y2;
        line[++pos]=(B){askx(x1),asky(y1),asky(y2),1};
        level[pos]=(C){asky(y1),askx(x1),askx(x2),1};
        line[++pos]=(B){askx(x2),asky(y1),asky(y2),-1};
        level[pos]=(C){asky(y2),askx(x1),askx(x2),-1};
    }
    
    build(1,pos-1,1);
    int ans=0,last=0;
    sort(line+1,line+pos+1,cmp);
    for(int i=1;i<=pos;i++)
    {
        modify(line[i].yl,line[i].yh-1,1,line[i].vl,2);
        int now=len[1];
        // cout<<i<<" "<<len[1]<<endl;
        ans+=abs(now-last);
        last=now;
    }
    build(1,pos-1,1);
    last=0;
    sort(level+1,level+pos+1,cnp);
    for(int i=1;i<=pos;i++)
    {
        modify(level[i].xf,level[i].xb-1,1,level[i].vl,1);
        int now=len[1];
        ans+=abs(now-last);
        last=now;
    }
    cout<<ans;
}

其他：

正如上文所言，扫描线是一种思想，我们可以把一些其他要维护的东西替换掉\(h\)，运用同样的思路推广出不同的解法

例题：P1502 窗口的星星

稍微点拨一下：

可以把星星的亮度和作为维护对象，把每个可以至少覆盖到这颗星星的位置看做一个矩形。
正解及代码请参考题解。

结语：

到这里，扫描线的入门部分就结束啦，作为一种思想，我们还需要把它运用到题目中才可以熟练掌握，另外的，扫描线还可以运用到其他坐标系问题中，比如二维数点，B维正交范围，当然，本文为扫描线入门，更高深的内容请移步dalao们的博客，等作者学习之后也会更，也许吧。

完结撒花~

都读到这里了，如果您觉得本文不错可以给个赞吗， rp++。