扫描线思想与算法实现

例题链接

给定平面直角坐标系内 $n$ 个四边平行于坐标轴的矩形，求其面积并。第 $i$ 个矩形的左下角和右上角分别为 $(x_{1,i},y_{1,i}),(x_{2,i},y_{2,i})$。

扫描线思想

扫描线，顾名思义，就是模拟一条线在平面上扫来扫去，从而得出答案。

这一般用于图特别大以致于无法存储的情况。

如图，图中描绘的就是扫描线从下至上扫过的情况。当坐标系非常大以致于无法存储时，就可以运用扫描线，模拟一条线扫过值域，扫的同时统计答案即可。

扫描线算法

接下来讲解如何具体实现扫描线算法，以维护矩形面积并为例。其余信息都是类似的。

指针扫过一维

很简单，使用一个指针每次自增即可。不妨令其从左至右扫过。

我们需要知道的就是当前这一列内被覆盖的长度 $\textit{len}_i$，答案即所有 $\textit{len}_i$ 之和。

数据结构维护一维

维护纵轴上的区间信息，一般使用线段树。

具体而言，我们需要使用线段树维护纵区间内的值，有两种操作：

区间加 $1$ 或区间减 $1$，且加/减区间两两对应。（见下文）
求根节点维护区间内非 $0$ 的数的个数。（如上文）

一般的线段树可能无法很好的维护此类信息，因为你并不知道减 $1$ 之后有多少数会变成 $0$。

但是扫描线用到的线段树具有一个很强的性质：加/减区间两两对应。

那么也就是说，加操作与其对应的减操作在线段树上操作的的节点互相对应。

因此可以考虑对于每一个节点 $i$，记 $\textit{cover}_i$ 表示 $i$ 对应区间被整体覆盖的次数，$\textit{len}_i$ 为 $i$ 对应区间内被覆盖的长度。

$\textit{cover}_i$ 并不会下传，因为这样可以确保加/减操作时正确操作 $\textit{cover}_i$，并且一一对应。

若 $\textit{cover}_i>0$，则必有 $\textit{len}_i$ 为对应区间长度。
否则，记 $\textit{lChild}_i,\textit{rChild}_i$ 分别为 $i$ 的左右子节点，有 $\textit{len}_i=\textit{len}_{\textit{lChild}_i}+\textit{len}_{\textit{rChild}_i}$。

这也是标记上传的逻辑。

为了便于表述，记矩形的左下角和右上角分别为 $(x_1,y_1),(x_2,y_2)$。

根据上文的图，因为此处是从左至右扫过，因此可以：

扫到矩形的左边界 $x_1$ 时将 $[y_1+1,y_2]$ 全部加上 $1$，代表这一段都被矩形覆盖了。
扫到矩形的右边界 $x_2$ 时将 $[y_1+1,y_2]$ 全部减去 $1$，代表这一个矩形结束了，之后都不会被这个矩形覆盖（但是仍然可能被其他矩形覆盖）。

注意矩形对应区间不是 $[y_1,y_2]$，而是 $[y_1+1,y_2]$。

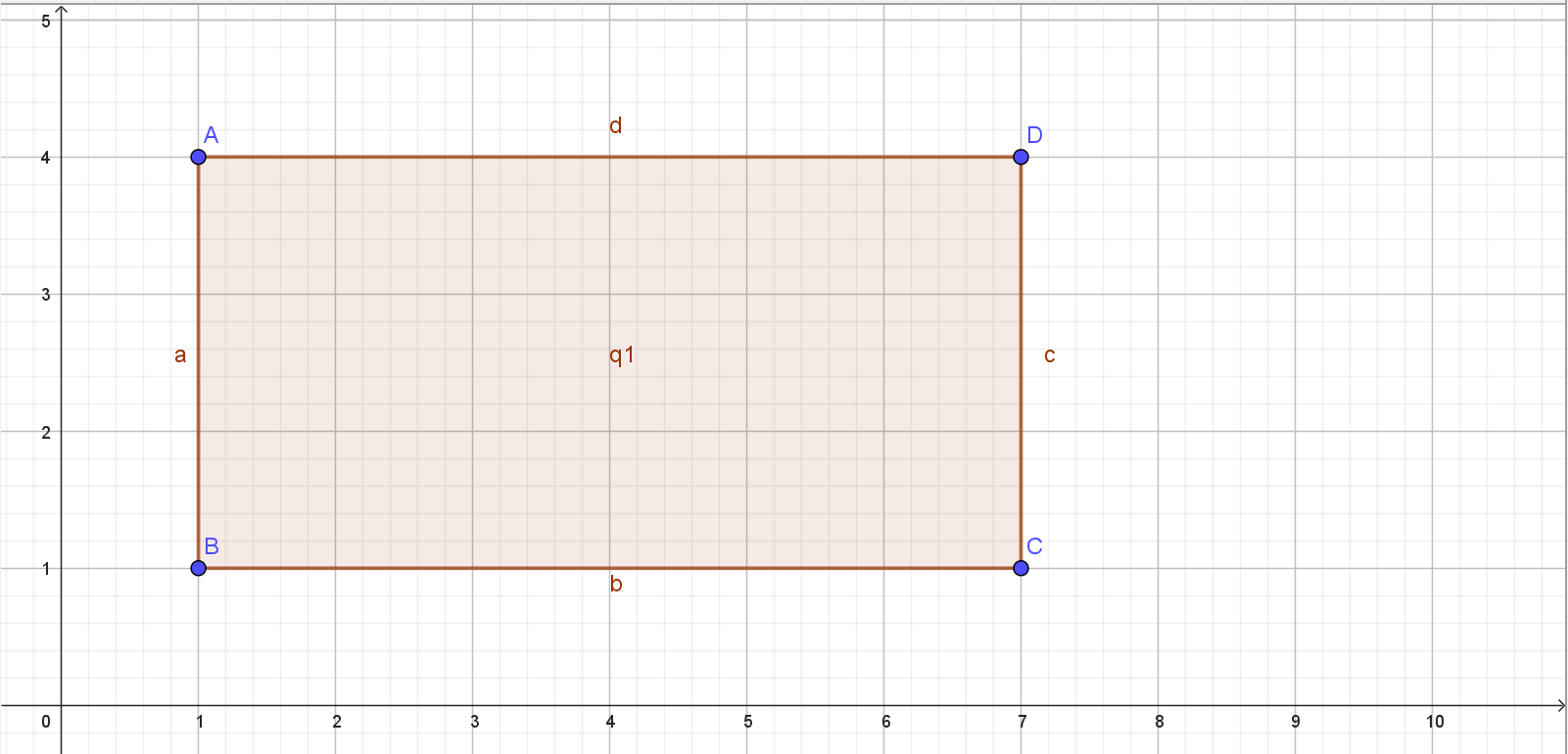
如图，$A(1,4),B(1,1)$，但是 $AB=4-1=3$，对应第 $2\sim 4$ 行。线段树维护的是第几行。（当然，你也可以说是 $1\sim 3$ 行，对应上文 $[y_1+1,y_2]$ 改为 $[y_1,y_2-1]$，但是没有本质区别，相当于整体偏移。）

这里提供一份参考代码。

参考代码

但是这份代码无法通过例题的任意测试点，因为所有测试点的 $x,y$ 都是跑满 $10^9$ 的。数组会越界。

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
typedef long long ll; 
constexpr const int N=1e5,V=1e5;
struct line{
	int l,r,w;
};
vector<line>q[N<<1|1];
struct segTree{
	struct node{
		int l,r;
		int len,cover;
	}t[N<<3|1];

	int size(int p){
		return t[p].r-t[p].l+1;
	}
	void up(int p){
		if(t[p].cover){
			t[p].len=size(p);
		}else{
			if(t[p].l==t[p].r){
				t[p].len=0;
			}else{
				t[p].len=t[p<<1].len+t[p<<1|1].len;
			}
		}
	}
	void build(int p,int l,int r){
		t[p]={l,r};
		if(l==r){
			t[p].cover=0;
			t[p].len=0;
			return;
		}
		int mid=l+r>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		up(p);
	}
	void add(int p,int l,int r,int k){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].cover+=k;
			up(p);
			return;
		}
		if(l<=t[p<<1].r){
			add(p<<1,l,r,k);
		}
		if(t[p<<1|1].l<=r){
			add(p<<1|1,l,r,k);
		}
		up(p);
	}
	int query(){
		return t[1].len;
	}
}t;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin>>n;
	static int x1[N+1],y1[N+1],x2[N+1],y2[N+1];
	for(int i=1;i<=n;i++){
		cin>>x1[i]>>y1[i]>>x2[i]>>y2[i];
	}
	for(int i=1;i<=n;i++){
		q[x1[i]].push_back({y1[i],y2[i],1});
		q[x2[i]].push_back({y1[i],y2[i],-1});
	}
	t.build(1,0,V);
	ll ans=0;
	for(int i=0;i<=V;i++){
		for(auto x:q[i]){
			t.add(1,x.l+1,x.r,x.w);
		}
		ans+=1ll*t.query();
	}
	cout<<ans<<'\n';
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

离散化

一般来讲，扫描线算法是需要离散化的。因为平面往往很大，超过 $10^6\times10^6$ 时往往需要离散化。

当然，线段树维护的纵区间可以不离散化，动态开点权值线段树维护即可；但是这样第一常数更大，第二横区间本来就要离散化，纵区间也可以顺带离散化。

记 $\operatorname{hashX}(x)$ 为排名为 $x$ 的原来的有效 $x$，$\operatorname{hashY}(y)$ 同理。

此时线段树维护的区间 $[l,r]$ 便是排名在 $[l,r]$ 内的有效 $y$。其区间长度为 $\operatorname{hashY}(r)-\operatorname{hashY}(l-1)$。注意不是 $\operatorname{hashY}(r)-\operatorname{hashY}(l)$。

同时，指针扫到 $i$ 时，这一整段相同的列的数量为 $\operatorname{hashX}(i+1)-\operatorname{hash}(i)$。

例题 AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
typedef long long ll; 
constexpr const int N=1e5,V=1e5;
struct line{
	int l,r,w;
};
vector<line>q[N<<1|1];
int hashX[N<<1|1],hashY[N<<1|1];
struct segTree{
	struct node{
		int l,r;
		int len,cover;
	}t[N<<3|1];
	
	int size(int p){
		return t[p].r-t[p].l+1;
	}
	void up(int p){
		if(t[p].cover){
			t[p].len=size(p);
		}else{
			if(t[p].l==t[p].r){
				t[p].len=0;
			}else{
				t[p].len=t[p<<1].len+t[p<<1|1].len;
			}
		}
	}
	void build(int p,int l,int r){
		t[p]={l,r};
		if(l==r){
			t[p].cover=0;
			t[p].len=0;
			return;
		}
		int mid=l+r>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		up(p);
	}
	void add(int p,int l,int r,int k){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].cover+=k;
			up(p);
			return;
		}
		if(l<=t[p<<1].r){
			add(p<<1,l,r,k);
		}
		if(t[p<<1|1].l<=r){
			add(p<<1|1,l,r,k);
		}
		up(p);
	}
	int query(){
		return t[1].len;
	}
}t;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	int n;
	cin>>n;
	static int x1[N+1],y1[N+1],x2[N+1],y2[N+1];
	for(int i=1;i<=n;i++){
		cin>>x1[i]>>y1[i]>>x2[i]>>y2[i];
	}
	for(int i=1;i<=n;i++){
		q[x1[i]].push_back({y1[i],y2[i],1});
		q[x2[i]].push_back({y1[i],y2[i],-1});
	}
	t.build(1,0,V);
	ll ans=0;
	for(int i=0;i<V;i++){
		for(auto x:q[i]){
			t.add(1,x.l,x.r-1,x.w);
		}
		
		ans+=1ll*t.query();
	}
	cout<<ans<<'\n';
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

posted @ 2025-08-09 11:04 TH911 阅读(45) 评论(0) 收藏举报

刷新页面返回顶部

TH911 Blog

光阴不可测，岁月亦无歌。