题解：[NOIP2024] 树的遍历

题目传送门

一道很好的 DP 思维题。

本文中「生成树」指代按照题目中方式生成的新树。

特殊性质

\(k=1\)

\(k=1\) 是简单的。

任意一个点，其临边都是树上的一条新链。

设 \(d_x\) 为 \(x\) 的度数，则答案为：

\[\prod_{i=1}^n(d_i-1)! \]

期望得分：\(\text{24pts}\)。

特殊性质 A

发现原图为一条链，可能的生成树有且仅有 \(1\) 种。（其实上面的代码写出来也可以过这一部分。）

期望得分：\(\text{4pts}\)。

朴素情况

发现对于 \(k\neq 1\) 的情况，从不同起始边得到的答案可能会有重复情况。

发现不好从不同的起始边找出重复情况（其实可以通过容斥找，但是我不会），于是可以从生成树的角度来找。

假设已经得到了一棵生成树，那么存在一个结论：所有可能的起始边构成了一条从原树叶节点到叶节点的链。

以样例二的三个生成树为例。统一使用红边表示可能的起始边，蓝边表示生成树。

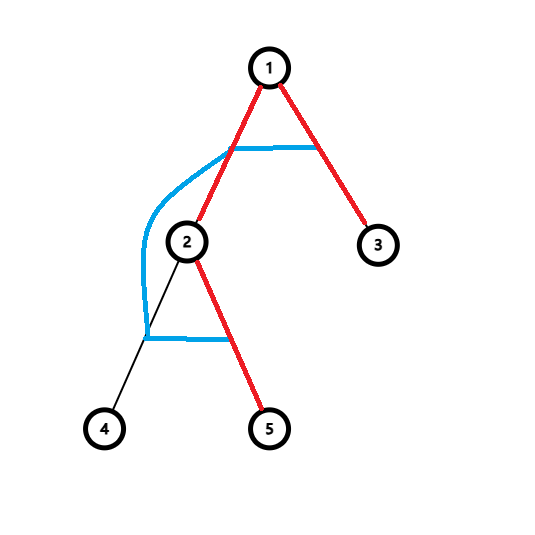
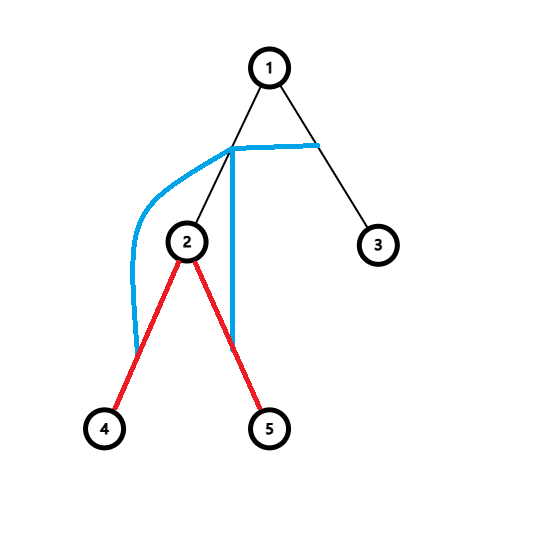
证明

首先，不可能存在三条可能的起始边相邻，否则不能保证生成树唯一。四条及以上同理。

其次，对于一条可能的起始边，其邻边中存在边也可以作为起始边，且这两条边在生成树上相隔一条边。因为你可以将生成顺序反过来生成。

故，一条可能的起始边若存在邻边，则一定存在一条邻边也是可能的起始边。故所有可能的起始边构成了一条链。

假设其不是叶节点到叶节点，则邻边仍然存在，不成立。

故，所有可能的起始边构成了一条从原树叶节点到叶节点的链。

设 \(V\) 表示链中节点，这条链满足：

• 从原树叶节点到原树叶节点。
• 链上至少一条边为关键边。

则，这条链产生的生成树数量为：

\[\dfrac{\displaystyle\prod_{i=1}^n(d_i-1)!}{\displaystyle\prod_{v\in V\land d_v\neq1}(d_v-1)} \]

因为起始边会确定方向，其贡献为 \((d_x-1-1)!\)。

设 \(S\) 为所有 \(V\) 构成的集合，则有答案 \(\textit{ans}\) 为：

\[\begin{aligned} \textit{ans}&=\sum_{V\in S}\dfrac{\displaystyle\prod_{i=1}^n(d_i-1)!}{\displaystyle\prod_{v\in V}(d_v-1)}\\ &=\left(\prod_{i=1}^n(d_i-1)!\right)\left(\sum_{V\in S}\prod_{v\in V\land d_v\neq1}(d_v-1)^{-1}\right) \end{aligned} \]

于是，问题就转化为了这样的问题：给定一棵树，树上边权为 \(0\) 或 \(1\)，求所有包含 \(1\) 的叶节点到叶节点的链上点权乘积之和。（\(x\) 的点权即 \((d_x-1)^{-1}\)）

树形 DP 即可求解。设 \(\textit{dp}_{x,1},\textit{dp}_{x,0}\) 为 \(x\) 子树内叶节点到 \(x\) 链上是否有 \(1\) 的点权乘积和。

设 \(x\) 的子节点分别为 \(y_1,y_2,y_3,\cdots,y_k\)。

特别地，为了化简运算，若 \((x,y_i)\) 权值为 \(1\)，则在计算 \(x\) 相关时，令：

\[\begin{aligned} \textit{dp}_{y_i,1}&\leftarrow\textit{dp}_{y_i,0}+\textit{dp}_{u_i,1}\\ \textit{dp}_{y_i,0}&\leftarrow0 \end{aligned} \]

有：

\[\begin{aligned} \textit{dp}_{x,0}&=(d_x-1)^{-1}\left([d_x=1]+\sum_{i=1}^k\textit{dp}_{y_i,0}\right) \\ \textit{dp}_{x,1}&=(d_x-1)^{-1}\sum_{i=1}^k\textit{dp}_{y_i,1} \end{aligned} \]

令 \(\textit{pl}_x\) 为合法情况数，有：

\[\textit{pl}_x=\sum_{i=1}^k\left(\left(\textit{dp}_{y_i,0}\sum_{j=1}^{i-1}\textit{dp}_{y_j,1}\right)+\left(\textit{dp}_{y_i,1}\sum_{j=1}^{i-1}\left(\textit{dp}_{y_j,0}+\textit{dp}_{y_j,1}\right)\right)\right) \]

那么就可以计算 \(\textit{ans}\)：

\[\begin{aligned} \textit{ans}&=\left(\prod_{i=1}^n(d_i-1)!\right)\left(\sum_{x=1}^n\textit{pl}_x(d_x-1)^{-1}\right) \end{aligned} \]

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=1e5,K=N-1,P=1e9+7;
int n,k,fact[N+1],inv[N+1];
int d[N+1];
vector<pair<int,int> >g[N+1];
bool flag[N+1];
int qpow(int base,int n){
	int ans=1;
	while(n){
		if(n&1){
			ans=1ll*ans*base%P;
		}
		base=1ll*base*base%P;
		n>>=1;
	}
	return ans;
}
void pre(){
	fact[0]=1;
	for(int i=1;i<=N;i++){
		fact[i]=1ll*fact[i-1]*i%P;
	}
	inv[N]=qpow(fact[N],P-2);
	for(int i=N-1;i>=0;i--){
		inv[i]=1ll*inv[i+1]*(i+1)%P;
	}
	for(int i=1;i<=N;i++){
		inv[i]=1ll*inv[i]*fact[i-1]%P;
	}
}
int dp[N+1][2];
void dfs(int x,int fx,int &ans){
	int pl=0;
	for(auto i:g[x]){
		int &v=i.first,w=flag[i.second];
		if(v==fx){
			continue;
		}
		dfs(v,x,ans);
		if(w){
			dp[v][1]=(dp[v][1]+dp[v][0])%P;
			dp[v][0]=0;
		}
		pl=(pl+1ll*(dp[x][0]+dp[x][1])%P*dp[v][1]+1ll*dp[x][1]*dp[v][0]%P)%P;
		dp[x][0]=(dp[x][0]+dp[v][0])%P;
		dp[x][1]=(dp[x][1]+dp[v][1])%P;
	}
	ans=(ans+1ll*pl*inv[d[x]-1])%P;
	if(d[x]==1){
		dp[x][0]=(dp[x][0]+1)%P;
	}
	dp[x][0]=1ll*dp[x][0]*inv[d[x]-1]%P;
	dp[x][1]=1ll*dp[x][1]*inv[d[x]-1]%P;
}
void Start(){
	for(int i=1;i<=n;i++){
		g[i].resize(0);
	}
	memset(d,0,sizeof(d));
	memset(flag,0,sizeof(flag));
	memset(dp,0,sizeof(dp));
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	pre();
	int c,T;
	cin>>c>>T;
	while(T--){
		Start();
		cin>>n>>k;
		for(int i=1;i<n;i++){
			int u,v;
			cin>>u>>v;
			d[u]++;d[v]++;
			g[u].push_back({v,i});
			g[v].push_back({u,i});
		}
		for(int i=1;i<=k;i++){
			int e;
			cin>>e;
			flag[e]=true;
		}
		if(n==2){
			cout<<"1\n";
			continue;
		}
		int ans=0;
		for(int i=1;i<=n;i++){
			if(d[i]>1){
				dfs(i,0,ans);
				break;
			}
		}
		for(int i=1;i<=n;i++){
			ans=1ll*ans*fact[d[i]-1]%P;
		}
		cout<<ans<<'\n';
	} 
	
	cout.flush();
	 
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}