【算法•日更•第十九期】动态规划:RMQ问题
▎前言
首先先来说一下RMB是什么,当然是人民币啦。
今天我们要学的这个东西不一般,叫做RMQ问题,那么它和RMB有什么关系呢?待小编细细说来。
▎前置技能:动态规划
不会的同志请戳这里迅速了解动态规划。
▎RMQ问题是什么
☞『定义』
RMQ (Range Minimum/Maximum Query)问题是指:对于长度为n的数列A,回答若干询问RMQ(A,i,j)(i,j<=n),返回数列A中下标在i,j里的最小(大)值,也就是说,RMQ问题是指求区间最值的问题。(copy自百度)
猜你也不想看,来,小编用人话翻译一下:就是说给定一堆数字(顺序位置固定且永远不变),(多次)询问你一段区间内的最大/最小值。
☞『问题解决:模拟算法』
RMQ只是一类这样的问题,却不是一门算法。
既然是问题,那么我们就应该解决,但是怎么解决,怎样解决,一切先从模拟算法(直白一点叫暴力)说起。
先来想想模拟算法怎么解决,当然是给定区间后直接遍历,寻找最大/最小值呗。但是别忘了,这种题多次询问,一直遍历对于数据规模大的题简直是杯水车薪。
此时,不得不请出动态规划。
☞『问题解决:动态规划』
我们为什么使用动态规划呢?先来思考这个问题:为什么暴力不能满足需求。
你肯定会说:这还不简单,暴力慢呗。
但是暴力究竟慢在了哪里?暴力慢在了没有完全利用好整个大区间,很多东西都在重复遍历。
那么什么东西能很好的利用大区间呢?我们就会自然的想到了动态规划(感觉属于区间动态规划)。
既然多次询问,那么就变向的告诉了我们一定要预处理,这里我们的动态规划可以O(n log n)预处理,然后O(1)查询。
先来思考怎么设计状态,最开始小编是这样想的,既然是区间型动态规划类问题,那么就让f[i][j]表示i~j区间内的最大/最小数吧,(以最大数为例)状态转移方程自然就是f[i][j]=max(f[i][k],f[k+1][j])。(k为随机一个i~j区间的数组下标,不过小编更喜欢取中点)
后来发现一本通提高篇上的设计状态更好,更快捷,我设计的太慢了。一本通提高篇上是这样处理的:f[i][j]表示i~2j-1区间内的最大/最小数,那么我们可以仿照之前我的想法,分一半,就是这样的:
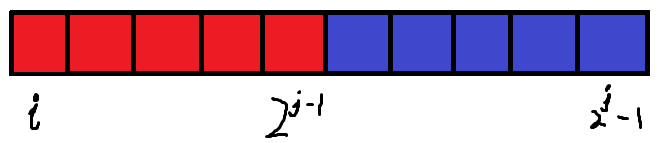
从区间初始和结束位置改成动态规划的形式后就是这样的:f[i][j-1]和f[i+2j-1][j-1],有时候奇数和偶数是不一样的,所以小编的图可能对这两个式子来说不太标准。
那么我们要求的最大最小值就很简单了。
但是问题又来了,我们如何面对询问呢?
我们可以以二为底,将这个区间内数字的个数次方(幂的逆运算)为界,进行比较两个区间大小,图解一下:
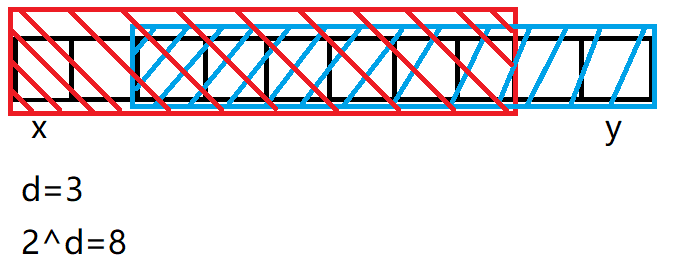
那么我们就只要比较出两个区间中的最大最小值即可。两个区间改成动态规划形式就是f[x][log[d]],f[y-(1<<log[d])+1][log[d]]),其中我把d改成了y-x+1的意思。
好了,问题又来了,log怎么处理,我们先来看一下前10个数的log处理情况:

经过专业调查和探寻后,就会发现log[i]=log[i/2]+1的规律,因此我们可以预处理出log的值。
☞『这么快的算法,为什么还需要其他算法呢?』
其实这个问题正是这个算法的弊端,因为不能支持期间修改一些数的值。
而线段树,树状数组正巧妙的解决了这一弊端。
▎实战演练:洛谷P1816 忠诚(模板题)
废话不多说,直接上题:
P1816 忠诚
题目描述
老管家是一个聪明能干的人。他为财主工作了整整10年,财主为了让自已账目更加清楚。要求管家每天记k次账,由于管家聪明能干,因而管家总是让财主十分满意。但是由于一些人的挑拨,财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚,他把每次的账目按1,2,3…编号,然后不定时的问管家问题,问题是这样的:在a到b号账中最少的一笔是多少?为了让管家没时间作假他总是一次问多个问题。
输入输出格式
输入格式:
输入中第一行有两个数m,n表示有m(m<=100000)笔账,n表示有n个问题,n<=100000。
第二行为m个数,分别是账目的钱数
后面n行分别是n个问题,每行有2个数字说明开始结束的账目编号。
输出格式:
输出文件中为每个问题的答案。具体查看样例。
输入输出样例
这道题相当好做,就是模板题,所以就不解释了,直接上代码:
1 #include<iostream> 2 using namespace std; 3 int m,n,a[100000],f[100000][100],x,y,log[100000]; 4 int main() 5 { 6 cin>>m>>n; 7 for(int i=1;i<=m;i++) 8 { 9 cin>>a[i]; 10 f[i][0]=a[i]; 11 } 12 for(int j=1;j<=16;j++) 13 for(int i=1;i+(1<<j)-1<=m;i++) 14 f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); 15 log[1]=0; 16 for(int i=2;i<=100000;i++) 17 log[i]=log[i/2]+1; 18 for(int i=1;i<=n;i++) 19 { 20 cin>>x>>y; 21 int d=y-x+1; 22 cout<<min(f[x][log[d]],f[y-(1<<log[d])+1][log[d]])<<" "; 23 } 24 return 0; 25 }
▎实战演练:一本通1541:【例 1】数列区间最大值(模板题)
废话不多说,直接上题:
1541:【例 1】数列区间最大值
时间限制: 1000 ms 内存限制: 524288 KB
提交数: 638 通过数: 224
【题目描述】
输入一串数字,给你 M 个询问,每次询问就给你两个数字 X,Y,要求你说出 X 到 Y 这段区间内的最大数。
【输入】
第一行两个整数 N,M 表示数字的个数和要询问的次数;
接下来一行为 N 个数;
接下来 M 行,每行都有两个整数 X,Y。
【输出】
输出共 M 行,每行输出一个数。
【输入样例】
10 2 3 2 4 5 6 8 1 2 9 7 1 4 3 8
【输出样例】
5 8
【提示】
数据范围与提示:
对于全部数据,1≤N≤105,1≤M≤106,1≤X≤Y≤N。数字不超过 C/C++ 的 int 范围。
【来源】
这道题只要把忠诚的代码改成max就可以了(还稍微有点其他细节),注意会卡常数,不能用cin和cout。代码如下:
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int m,n,a[1000000],f[1000000][100],x,y,log[1000000]; 5 int main() 6 { 7 scanf("%d%d",&m,&n); 8 for(int i=1;i<=m;i++) 9 { 10 scanf("%d",&a[i]); 11 f[i][0]=a[i]; 12 } 13 for(int j=1;j<=18;j++) 14 for(int i=1;i+(1<<j)-1<=m;i++) 15 f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 16 log[1]=0; 17 for(int i=2;i<=m;i++) 18 log[i]=log[i>>1]+1; 19 for(int i=1;i<=n;i++) 20 { 21 scanf("%d%d",&x,&y); 22 int d=y-x+1; 23 printf("%d \n",max(f[x][log[d]],f[y-(1<<log[d])+1][log[d]])) ; 24 } 25 return 0; 26 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号