【半导体物理 | 笔记】第四章 半导体的导电性
一、载流子的漂移运动和迁移率
欧姆定律
电导率 \(\sigma =\dfrac{1}{\rho}\)
欧姆定律微分形式 \(J=\sigma \mathscr{E}\)
漂移速度和迁移率
迁移率 \(\mu=\left|\dfrac{\bar{v}_\mathrm d}{\mathscr E}\right|\)
\(J=nq\mu\mathscr E\)
\(\sigma =nq\mu\)
半导体的电导率和迁移率
\(J=J_\mathrm n+J_\mathrm p=(nq\mu_\mathrm n+pq\mu_\mathrm p)\mathscr E\)
\(\sigma=nq\mu_\mathrm n+pq\mu_\mathrm p\)
二、载流子的散射
载流子散射
-
载流子热运动不断遭受散射
-
平均自由程:连续两次散射间自由运动的平均路程
-
平均时间:连续两次散射间的平均时间
散射率\(P\):单位时间内一个载流子遭到散射的次数
半导体的主要散射机构
- 电离杂质散射(主要)
\(P_\mathrm i\propto N_\mathrm iT^{-3/2}\)
\(N_\mathrm i\):总杂质浓度
- 晶格振动声学波散射(主要)
\(P_\mathrm s\propto T^{3/2}\)
-
其他因素
-
晶格振动光学波
-
等能谷散射
-
中性杂质散射
-
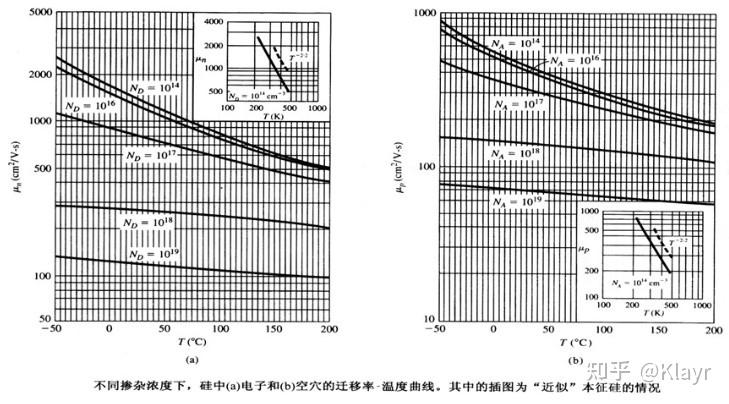
三、迁移率与杂质浓度和温度的关系
平均自由时间和散射概率的关系
电导率、迁移率与平均自由时间的关系
\(\mu_\mathrm n=\dfrac{q\tau_\mathrm n}{m^*_\mathrm n},\mu_\mathrm p=\dfrac{q\tau_\mathrm p}{m^*_\mathrm p}\)
\(m^*_\mathrm n,m^*_\mathrm p\):电导有效质量(各向异性)
迁移率与杂质和温度的关系

-
杂质浓度较低时,电子(空穴)的多子迁移率和少子迁移率趋近于相同的值
-
杂质浓度增大时,电子与空穴的多子和少子迁移率都单调下降
-
对给定杂质浓度,电子与空穴的少子浓度均大于相同杂质浓度下的多子迁移率
-
相同杂质浓度下少子迁移率与多子迁移率的差距随杂质浓度的增大而减小
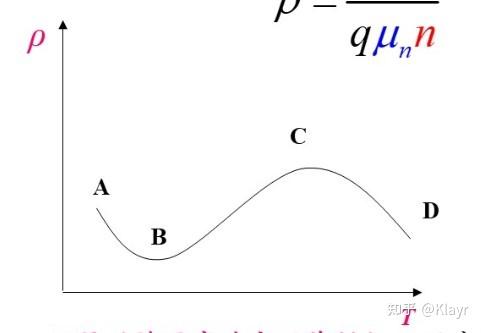
四、电阻率及其与杂质浓度和温度的关系
电阻率和杂质浓度的关系
电阻率随温度的变化
- 三段
![]()
五、强电场下的效应、热载流子
欧姆定律的偏移
\(T_\mathrm e\):热载流子温度
六、多能谷散射、耿氏效应
n型砷化镓在强场下半导体内部电流以很高频率振荡
用于微波转移电子器件




 浙公网安备 33010602011771号
浙公网安备 33010602011771号