CSP-S & NOIP 2025 游记
省流:在排序面前一败涂地。
选手屡次在考场上重新发明轮子。
Day -INF
打 SCP-S 228 pts,打 T2 的时候发现本地跑 \(O(n\log n)\) TLE,于是想怎么进行 \(O(n)\) 排序,不知道为什么没有想到桶排,还好没有被卡常。
CSP-S
Day 1
打 CSP-S T2,发现复杂度差不多能容纳 \(O(nk2^k)\),只要发明一个 \(O(n)\) MST 算法即可!不知道为什么场上没想到外面排序里面归并,也同样没有想到先跑一遍 Kruskal 去掉多余边,连着两场都被排序算法击败了,我无敌了。然后一直在死磕 Prim,但是不知道为什么考场的 \(O(n\log m)\) 跑得奇慢无比,再加上外面套的 \(O(k2^k)\) 预估得分不超过 \(10\)。
由于冲不出来 T2 导致心态爆炸,哈哈哈只能等 NOIP 翻盘了,预估分段 \([100,130]\),真是艰苦卓绝啊。
反思:考试心态问题,T2 由于强制自己想到复杂度不与 \(m\) 相关的 MST 做法而一直死在一条死路上,且无法花费更多时间后续推进,没有坚持 Kruskal 做法,没有往下推想到优化。启示应该多尝试不同的思路并向下顺延至较深层次,不要一直被卡住。
UPD:选手发现自己离切 T3 只有几厘米,破防了。
UUPD:选手发现自己的 T2 Prim 写的实际上是 \(O(2^k(n+m+k)\log m)\) 的,这玩意 \(2\times 10^{10}\),跑第三个大洋里跑了 \(117.4s\),居然跑出了正确答案我是没想到的。选手场上没有想到缩边不知道选手在干什么。
UUUPD:选手挂了 \(-36\) 分,还能进 NOIP,也是欣慰了。
反思:选手不相信自己能够切出 T3/4 因此硬冲 T2 陷入僵局。
感觉还是写个题解。
T1
开场 \(\text{15min}\) 左右切的,同样写了 \(3\) 个堆,但是比较另类的是大家要么动态用堆做要么离线用排序做反悔贪心,我直接离线用堆做(?。感觉这些个堆写得有点何意味,不伦不类了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N][3],buk[3],rk[3],now;
priority_queue<int,vector<int>,greater<int> >q[3];
bool cmp(int x,int y){return a[now][x]>a[now][y];}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int Tn;cin>>Tn;
while(Tn--){
cin>>n;int ans=0;
buk[0]=buk[1]=buk[2]=0;
for(now=1;now<=n;now++){
for(int j=0;j<3;j++)
cin>>a[now][j],rk[j]=j;
sort(rk,rk+3,cmp);
ans+=a[now][rk[0]];
q[rk[0]].push(a[now][rk[0]]-a[now][rk[1]]);
buk[rk[0]]++;
}
for(int j=0;j<3;j++){
while(buk[j]>n/2){
ans-=q[j].top();
q[j].pop();
buk[j]--;
}
while(!q[j].empty())q[j].pop();
}
cout<<ans<<'\n';
}
return 0;
}
T2
好像关于本题的失败上面写得已经够多了。首先不知道为什么选手一开始想了先对原树跑一边 MST 但是又觉得这样可能会有问题?(有问题在哪儿?)因为一开始开的思路是一条边 \((u,v,w)\) 可以被 \((u,v,a_{i,u}+a_{i,v})\) 代替,考试完发现不知道自己当时在想什么还想了高达 3h。这玩意跟原边完全没有关系,为什么要保留 \(m\) 条边。再者其实一开始这样转化就有问题,因为最终要形成最小生成树可能出现一个 \(c_i\) 上面接了多个并列连通块的情况,贡献会算重。
想到这些乱七八糟的东西时选手就应该考虑化繁为简了,即回归最朴素的 MST。选手开场观察数据范围,发现 \(O(n2^k)\) 左右可以直接通过。于是选手在草稿纸上写下,发明一个 O(n) 的 MST 算法即可!,笑死我了。发现 Kruskal 的瓶颈其实在于带一只 \(\log\) 的排序,因此在外面排好里面归并,或者直接在外面排好然后枚举 \(2^k\) 的时候直接忽略非法边就能直接做到 \(O(2^k (n\alpha(n)+nk))\)。
内部归并
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+15,M=1e6+5;
const LL INF=1e15;
LL ans=INF;
int n,m,k,c[N],cpt,fa[N];
struct Edge{int u,v,w;}Re[M],e[N],E[12][N];
Edge A[N+10*N],C[N+10*N];
bool cmp(Edge x,Edge y){return x.w<y.w;}
inline int fr(int x){return fa[x]==x?x:fa[x]=fr(fa[x]);}
bool ins(int x,int y){
int frx=fr(x),fry=fr(y);
if(frx==fry)return 0;
fa[frx]=fry;return 1;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u,v,w;cin>>u>>v>>w;
Re[i]=(Edge){u,v,w};
}
sort(Re+1,Re+1+m,cmp);
for(int i=1;i<=m;i++)
if(ins(Re[i].u,Re[i].v))
e[++cpt]=Re[i];
m=cpt;
for(int i=1;i<=k;i++){
cin>>c[i];
for(int j=1;j<=n;j++){
int v=j,w;cin>>w;
E[i][j]=(Edge){i+n,v,w};
}
sort(E[i]+1,E[i]+1+n,cmp);
}
for(int S=0;S<(1<<k);S++){
LL res=0;int cnt=cpt;
for(int i=1;i<=m;i++)
A[i]=e[i];
for(int i=1;i<=n+k;i++)
fa[i]=i;
for(int i=1;i<=k;i++)
if((S>>(i-1))&1){
res+=c[i];
int pos=1,omg=1;
for(int j=1;j<=n;j++){
while(pos<=cnt&&A[pos].w<=E[i][j].w)
C[omg++]=A[pos++];
C[omg++]=E[i][j];
}
while(pos<=cnt)C[omg++]=e[pos++];
cnt=omg-1;
for(int j=1;j<=cnt;j++)
A[j]=C[j];
}
for(int i=1;i<=cnt;i++)
if(ins(A[i].u,A[i].v))
res+=A[i].w;
ans=min(ans,res);
}
cout<<ans;
return 0;
}
无归并
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+15,M=1e6+5;
const LL INF=1e15;
LL ans=INF;
int n,m,k,c[N],cpt,fa[N];
struct Edge{int u,v,w;}Re[M],e[N];
bool cmp(Edge x,Edge y){return x.w<y.w;}
inline int fr(int x){return fa[x]==x?x:fa[x]=fr(fa[x]);}
bool ins(int x,int y){
int frx=fr(x),fry=fr(y);
if(frx==fry)return 0;
fa[frx]=fry;return 1;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>k;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u,v,w;cin>>u>>v>>w;
Re[i]=(Edge){u,v,w};
}
sort(Re+1,Re+1+m,cmp);
for(int i=1;i<=m;i++)
if(ins(Re[i].u,Re[i].v))
e[++cpt]=Re[i];
for(int i=1;i<=k;i++){
cin>>c[i];
for(int j=1;j<=n;j++){
int v=j,w;cin>>w;
e[++cpt]=(Edge){i+n,v,w};
}
}
sort(e+1,e+1+cpt,cmp);
for(int S=0;S<(1<<k);S++){
LL res=0;
for(int i=1;i<=n+k;i++)
fa[i]=i;
for(int i=1;i<=k;i++)
if((S>>(i-1))&1)res+=c[i];
for(int i=1;i<=cpt;i++){
if(e[i].u>n&&(!((S>>(e[i].u-n-1))&1)))continue;
if(ins(e[i].u,e[i].v))
res+=e[i].w;
}
ans=min(ans,res);
}
cout<<ans;
return 0;
}
T3
选手看这题的时候想到了自己曾经说过,我如果在 CSP 考场上看到字符串题绝对第一时间想哈希。想到了对 \(t_1,t_2\) 进行最长公共前后缀缩串,先打了个哈希的暴力(大概 \(O(nL_2)\)?),然后确实想了一会儿 ACAM,因为考试前才打过且感觉这个题挺可做的。选手想了想发现自己无法解决匹配问题,且如果要计算方案数可能还要搞个二维数点之类的东西,因为要分别对 \(1,2\) 跑 ACAM(选手不知道为什么没有想到把 \(s_1,s_2\) 也缩了,然后放在一起跑),然后继续磕哈希直接倒闭了。
结果选手考完看了一眼题解直接 \(\text{20min}\) 切了这个东西。不知道为什么那么显然的东西想不到。发现 \(s_1,s_2\) 不同的地方对应着 \(t_1,t_2\) 也不同,除此之外 \(t_1,t_2\) 的所有位置都相同。因此直接把 \(t_1,t_2\) 拆成 \(A?BC?D\) 的形式,其中 \(t_1\) 表示为 \(ABD\),\(t_2\) 表示为 \(ACD\),\(A,D\) 分别为最长公共前/后缀。\(s_1,s_2\) 也这样拆,判一下 \(|t_1|\neq |t_2|\) 然后直接跑多模匹配即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=2e5+5,L=6e6+5;
int n,qn,ncnt;
struct Node{int ch[27],cnt,fail;}t[L];
void ins(string s){
int now=0,len=s.size();
for(int i=0;i<len;i++){
int p=(s[i]>='a'&&s[i]<='z'?s[i]-'a':26);
if(!t[now].ch[p])t[now].ch[p]=++ncnt;
now=t[now].ch[p];
}
t[now].cnt++;
}
int hd,tl,q[L],num[L];
void build(){
hd=1,tl=0;
for(int p=0;p<27;p++)
if(t[0].ch[p])q[++tl]=t[0].ch[p];
while(hd<=tl){
int now=q[hd++];
num[now]=t[now].cnt+num[t[now].fail];
for(int p=0;p<27;p++){
if(t[now].ch[p])t[t[now].ch[p]].fail=t[t[now].fail].ch[p],
q[++tl]=t[now].ch[p];
else t[now].ch[p]=t[t[now].fail].ch[p];
}
}
}
string brk(string &a,string &b){
string A,B,C,D;
int L=1,R=a.size(),m=a.size();
for(int j=1;j<=m;j++)
if(a[j-1]!=b[j-1]){L=j;break;}
for(int j=m;j>=1;j--)
if(a[j-1]!=b[j-1]){R=j;break;}
int siz=R-L+1;
A=a.substr(0,L-1);B=a.substr(L-1,siz);
C=b.substr(L-1,siz);D=a.substr(R,m-R+1);
string my=A+"#"+B+C+"#"+D;
return my;
}
int query(string s){
int len=s.size(),res=0,now=0;
for(int i=0;i<len;i++){
int p=(s[i]>='a'&&s[i]<='z'?s[i]-'a':26);
now=t[now].ch[p];
res+=num[now];
}
return res;
}
int main(){
//freopen("replace.in","r",stdin);
//freopen("replace.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>qn;
for(int i=1;i<=n;i++){
string sa,sb,A,B,C;cin>>sa>>sb;
if(sa==sb)continue;
ins(brk(sa,sb));
}
build();
while(qn--){
string ta,tb;cin>>ta>>tb;
if(ta.size()!=tb.size()){
cout<<'0'<<'\n';
continue;
}
else cout<<query(brk(ta,tb))<<'\n';
}
return 0;
}
T4
感觉好题。感觉设出了大约正确的方程。感觉被 T2 击溃了不敢往后拼。
Solution1(贡献延后)
搬个出题人题解,感觉这种设计挺少见的,有点 Ad-hoc 那味了。下文是来自 2025/11/13 UPD 的较详细的题解和可能入手的解题思路。
Observation
显然我们无法 \(O(n!)\) 地枚举每种情况,一定要通过某种计数/DP 来描述这个过程。发现我们有两种选择的方式:
-
对于每个人,考虑他放在排列中的哪个位置。这样做是没有前途的,因为一个位置放人会产生后效性,记录哪些位置放了人显然是一个很高复杂度的东西。
-
对于每个位置,考虑哪个人放在这个位置上。这看起来挺可做的,我们来仔细分析一下:
考虑不断往后放,令当前放到第 \(i\) 位,且 \([1,i]\) 中放的位置有 \(j\) 个被拒绝了,方案数 \(f_{i,j}\)。这些被拒绝的位置要么是 \(S_{i'}=0\),要么是他耐心不够。
考虑进行转移。对于 \(i\to i+1\),我们需要为 \(i+1\) 位定一个人。如果 \(S_i=0\),随便选哪个都会被拒绝。重点考虑 \(S_i=1\) 的情况:
-
如果我们要选一个能被录取的人 \(p\),其耐心需要满足 \(c_p>j\)。
-
如果我们要选一个不能被录取的人 \(p\),其耐心需要满足 \(c_p\le j\)。
我们不妨把这个过程放在一个关于 \(c\) 的桶上,改变一下 \(c_j\) 的定义,让新的 \(c_j\) 表示原来耐心为 \(j\) 的人数,并关于 \(c\) 做一个前缀和 \(pre_j=\sum_{k=0}^j c_j\)。
那么对于选能被录取的人,我们选的就是 \([j+1,n]\text{ 中未被选择的人数量}=pre_n-pre_j-[j+1,n]\text{ 中被选择的人的数量}\),是 \(c\) 值域上的一段后缀。
对于选不能被录取的人,我们选的就是 \([1,j]\text{ 中未被选择的人数量}=pre_j-[1,j]\text{ 中被选择的人的数量}\),是 \(c\) 值域上的一段前缀。
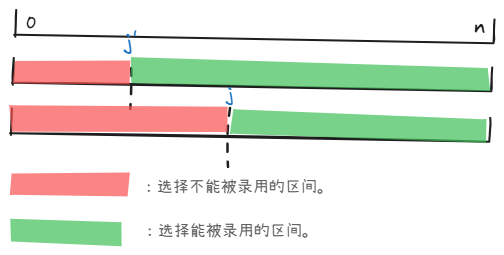
发现这个东西也是有后效性的。如果你随便乱选,你无法确定前面有多少个选在了你需要选的区间(\([1,j]\) 或 \([j+1,n]\) 中)。那我们不妨先只选不录用的即一段前缀(具体原因之后再说),对于将要录用的(我们肯定要选一个人),使用贡献延后 trick,暂时不决定他,等到之后再决策。
Analysis
根据前面的思路,先做一个前缀和,让 \(c_i\) 表示针对真实的 \(c\) 开的一个桶,然后 \(pre_j=\sum_{i=0}^j c_i\)。这样可以快速计算全局耐心 \(\le j\) 的人数。然后考虑转移。
考虑 \(S_{i+1}=1\),我们要往 \(i\) 个人里面多塞一个。
考虑设 \(f_{i,j,k}\) 表示已面试 \(i\) 个人,有 \(j\) 个被拒绝/逃走,\([1,i]\) 中有 \(k\) 个位置是已经确定的,这些位置上每个人的耐心都 \(\le j\),且剩下没填的位置填的人耐心都应该 \(>j\)。需要注意的是,由于贡献延后,\([1,i]\) 这些人中可能存在一些空的位置,即之前选的将要被录用的人的位置,数量即为 \(i-k\)。
考虑 \(S_{i+1}=1\),如果这个人被同意,说明一定有耐心 \(>j\),直接选用 \(f_{i,j,k}\to f_{i+1,j,k}\),留空一个位置,其条件是 \(n-pre_j>i-k\),即耐心 \(>j\) 的人数不为 \(0\)。
若被拒,我们在前面还未被决策的 \(pre_j-k\) 个点中选一个,同时决定前面 \(i-k\) 个空位我们填什么人上去。即我们要从下图绿色部分中找到耐心为 \(j+1\) 的 \(l\) 个人,然后把他们填到 \(i-k\) 个空位中的 \(l\) 个上。对于没有被填上去的人,他们将会成为后续被选择的 \(\le j'\) 的不被录用的人。
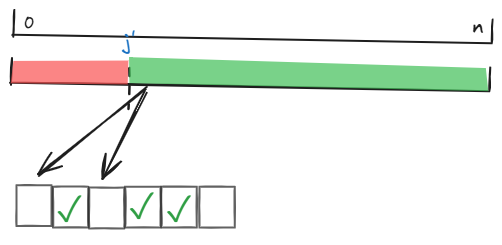
\(k\) 维加的 \(l+1\) 中 \(l\) 是填充的空位数,\(1\) 就是我们填充了第 \(i+1\) 位为前缀中某个未被录用的人。由于每个人本质不同,需要在转移中 \(\times l!\)。
讨论 \(S_{i+1}=0\) 的情况,发现我们无论怎么选都会导致被拒人数 \(+1\),那么无论如何我们都要挑出 \(l\) 个耐心为 \(j+1\) 的人填前面 \([1,i]\) 中的 \(i-k\) 个空位,那我们直接在上面的方程基础上改即可。
我们发现这个分类稍有不同。因为填第 \(i+1\) 位时,可能选到 \(j+1\),而在 \(S_i=1\) 的情况中,我们只把 \(j+1\) 贡献到了 \([1,i]\) 的空位中。那我们换一下分类角度,依据为 \(i+1\) 位是否立刻被决策。如果填耐心 \(>j+1\) 的人,一定不会立刻被决策,转移条件 \(n-pre_{j+1}>i-k-l\):
否则选 \(\le j+1\),则我们可以在 \(pre_{j+1}-k-l\) 中抽取任意一个作为当前选的东西,其中 \(l\) 个贡献给了 \(i-k\) 个空位,也可能抽到 \(j+1\):
这时候就可以回答前面的问题了,为什么要选一段前缀。因为随着 \(i\) 的递增,\(j\) 不减,所有后面处理的前缀都包含前面的前缀,所以前面前缀选的数量可以直接被减掉,不会产生后效性。
最后统计答案。我们已经保证了所有 \(\le j\) 的点都被填上了人,即耐心 \(\le j\) 的都被填到了排列中的某个位置,那么剩余的人必定恰好填在空位上,只需乘上剩余排列数即可,答案即为 \(\sum_{j=0}^{n-m}(n-pre_j)!f_{n,j,pre_j}\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=998244353;
const int N=505;
int n,m,c[N],pre[N];
LL f[N][N],tmp[N][N],jc[N],C[N][N];
char s[N];
void add(LL &x,LL y){x=(x+y>=MOD?x+y-MOD:x+y);}
int main(){
//freopen("employ.in","r",stdin);
//freopen("employ.out","w",stdout);
scanf("%d%d",&n,&m);
scanf("%s",s+1);
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
c[x]++;
}
pre[0]=c[0];jc[0]=1;
for(int i=1;i<=n;i++)
pre[i]=c[i]+pre[i-1],
jc[i]=jc[i-1]*i%MOD;
for(int i=0;i<=n;i++)
C[i][0]=C[i][i]=1;
for(int i=2;i<=n;i++)
for(int j=1;j<i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD;
f[0][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<=n;j++)
for(int k=0;k<=n;k++)
tmp[j][k]=f[j][k],f[j][k]=0;
for(int j=0;j<=i;j++){
for(int k=0;k<=pre[j]&&k<=i;k++){
if(s[i+1]=='0'){
for(int l=0;l<=c[j+1]&&l<=i-k;l++){
if(n-pre[j+1]>i-k-l)add(f[j+1][k+l],tmp[j][k]*
C[c[j+1]][l]%MOD*C[i-k][l]%MOD*jc[l]%MOD);
add(f[j+1][k+l+1],tmp[j][k]*(pre[j+1]-k-l)%MOD*
C[c[j+1]][l]%MOD*C[i-k][l]%MOD*jc[l]%MOD);
}
}
else {
if(n-pre[j]>i-k)add(f[j][k],tmp[j][k]);
for(int l=0;l<=c[j+1]&&l<=i-k;l++)
add(f[j+1][k+l+1],tmp[j][k]*(pre[j]-k)%MOD*
C[c[j+1]][l]%MOD*C[i-k][l]%MOD*jc[l]%MOD);
}
}
}
}
LL ans=0;
for(int j=0;j<=n-m;j++)
add(ans,f[j][pre[j]]*jc[n-pre[j]]%MOD);
cout<<ans;
return 0;
}
Solution2(容斥)
已收录至部分 DP 问题小记 计数、容斥原理。
Summary
选手确实感觉今年 CSP-S 是比较可做的一场,但是发挥不好说是,原因也挺多的,先这样吧/oh,备战 NOIP。大约是正赛经验不够丰富吧,做出如下反思:
-
正式比赛中没有冷静下来想题,完全处于一个一眼秒/骗分的状态,对自己的观察和推导不够自信,没有深入往下,确实尝试了很多种解法但是每种都没有深入,需要调整下一场正赛心态。
-
没有尽全力拿部分分(没有认真思考只是扫了一眼),部分题目坚持了错解导致得分极低的情况,死磕某道题。事实上相信在 4h 够用的情况下需要放松身心理解题意后揣测而不是主观主导自己的思维框架。
-
做题经验不够丰富/充分,套路化的双串转单串匹配(T3)或使用前缀后缀同步匹配的二维数点(T3)都是可行解法,双向转单向容斥/贡献延后 DP(T4)都是可行解法(尝试从多角度做出转化,抓住题目性质),见过的 trick 不够多吧,短时间内可能难以修正。
-
计数相关练习欠缺。
消极的话自己藏起来吧。
NOIP
Day -1
simonG 及 ct 等学长来分享经验。其中 ct 曾言,真正退出 OI 离开自己热爱的东西时感觉自己也不剩什么了,生活中特别热爱的东西。后来听 Little_corn 说他 CS2 非常 nb 还有枪皮,事实证明人很擅长否定自己的生活。现在回首,确实挺欣慰的,毕竟自己生活中还有音乐的存在,可以偶尔自行演奏解乏,学 OI 的路上留给后人一车 blog。感觉这个 blog 还挺热闹的,不少文章都有 \(\geq 5\) 评论,特此感谢 Little_corn,cjrqwq 等人指出更优做法并对部分文章内容加以探讨,使其更加完善。
Day 0
\(\text{The way,}\)
\(\text{To celebrate.}\)
\(\text{I’ll be waiting}\)
\(\text{Till we make it}\)
\(\text{The day,}\)
\(\text{To celebrate.}\)
\(\text{I’ll be waiting}\)
\(\text{Till we make it.}\)
\(\text{Oh——}\)
\(\text{We will see,}\)
\(\text{Come with me take the journey.}\)
\(\text{Oh——}\)
\(\text{We will see,}\)
\(\text{Come with me take the journey.}\)
——HOYO-MiX / Anthony Lynch《踏上旅途 Take the Journey》
下午到希尔顿酒店,放东西,吃围餐。酒店双床房疑似短缺,又喜获神秘大床 + 折叠床房,承蒙舍友 Soh_paraMEEMS 的照顾体谅,因身体条件不适使用了大床。一直受 Soh _paraMEEMS 照顾谦让,在此表示诚挚感谢与抱歉。
larsr 和 _Cheems 在反复测试茶水的表面张力(?。晚上去酒店自习室自习,没有带电脑,大悲。这周开始时才感觉到有点不舒服,到酒店了直接加剧,很快就喉咙疼得说不出话来了。爸妈远程叫我美团买头孢克洛和布洛芬,睡前吞了两片头孢,喝两支双黄连然后就躺下了。
Soh_paraMEEMS 九点多回来。我挺难受的躺床上什么也不想复习,然后直接看书。看到 \(22:10\) 左右 para 差不多也啥都干完了,然后就直接睡了。夜里醒了一次然后就睡不着了,慢慢迷糊了一下精神天就亮了。
Day 1
\(\text{6:20}\) 酒店电话起床,迷迷糊糊坐了 \(\text{15min}\) 才想起来要起床。吃早餐,上大巴,去中山纪中。
吃完药好点但还是很难受,在下面咳了一会儿才上考场。开考前 \(\text{30min}\) 和 _Cheems 苦于本栋找不到厕所(满人),询问保安速通隔壁楼进行一个厕所的上,回来大概还有 \(\text{15min}\)。
开考,此时感觉自己异常平静,大概是疼傻了。看了看所有题,T3,T4 容易看懂(?。回来看 T1,想到点什么神秘贪心,试了试拆了拆,大概调了 \(\text{50min}\) 才通过 candy6.in 和 candy7.in。以为自己通过了,然后就丢掉没管了。赛后发现自己可能有一部分假了,破防。
我赛时 T1 干了什么
感觉可以把最终答案刻画成每两个相同商品打包成一组,然后加上若干个独立的 \(x_i\)。每个 \(x_i\) 最多会被选 \(1\) 次,而打包可以选任意次。其价值只有 \(1,2\) 两种。
可以直接找最小的 \(z_i=x_i+y_i\) 然后最后选若干次这个。前面先把 \(x_i\le \frac{\min z_i}{2}\) 的选完,因为任意出现一对 \(x_i+x_j\geq \min z_i(i\neq j)\) 都可以直接选 \(z_i\) 替代。然后这样不优仅当容积利用不充分。考虑试着撤掉一个最大的 \(x_i\) 是否能使答案更大。
我认为这个思路存在问题在于,出现任意一对都可以直接选 \(z_i\) 替代,所以其可能能够容纳一个 \(x_i>\frac{\min z_i}{2}\) 的商品。然而我在场上并没有加入如上判断就通过了所有大样例,现在很慌。且在 Luogu 上不判断该情况也可以通过此题。
希望不要有人想到卡这个东西。
继续看 T2,神秘数数题,看不懂题,不全选 \(V=1\) 就行了吗(\(V\) 是占用空间)。哦原来是使得策略在当前方案下最优啊,看了半天样例解释才看明白。然后思考怎么做,发现样例解释给了很好的启发:按照 \(a\) 降序排序,存在一个三元组 \((x,y,z)(x<y<z)\) 使得 \(a_x\) 是第一个不选的 \(V=2\),\(a_y,a_z\) 是最后两个选的 \(V=1\),注意要特判一下 \(z\) 不存在的情况可能也合法。
其非法充要条件为实际选的顺序为 \((y,x,z)\),又由于性价比相同时一定会先选 \(V=2\),所以非法当且仅当 \(a_x>\frac{a_y}{2}>a_z\) 且 \(a_x>a_y+a_z\)(正难则反),即选 \(y,z\) 严格劣于选 \(x\)。其情况当且仅当前面已经选了 \(m-2\) 的容积,只剩 \(2\) 的容积了。这个显得 \(m=2\) 的部分分比较有启发性。
\(z\) 对于 \(y\) 的数量可以简单后缀和预处理,\([1,y)\) 和 \((z,n]\) 都是随便选,考虑 \(O(n^2)\) 固定 \(x,y\),然后 \(z\) 可以二分确定,总的变成了 \(O(n^2\log n)\)。如果顺序推 \(y\) 指针可以直接优化掉找第一个合法 \(z\),回到 \(O(n^2)\)。
最后需要处理 \((x,y)\) 间存在的不确定个数的已选 \(1\) 对已选容积做出贡献,如果暴力枚举其个数 \(k\) 可以用组合数做到 \(O(n^3)\),原地起飞。选手调了半天这个做法,到 \(11:00\) 发现自己毫无进展,强制自己 \(\text{20min}\) 打了个指数暴力,然后跑去拼好分了。
发现自己后面的题也不怎么会,凹了一会 T3 发现假了,打了个 \(\text{树高}=2\) 然后跑路。T4 感觉挺友好,又因为练了一点 DS 尝试分配了 \(\text{20min}\) 凹了一下,发现点数是 \(O(n^2)\) 的,这样记录还要对于每个 \(i\) 区间 \(\text{checkmax}\),预处理就是 \(O(n^2\log n)\) 的,我也不知道这玩意能过个啥。查询不想写什么 ST 表了直接暴力查,\(O(qn^2)\) 原地起飞,预计得分 \(\text{5pts}\)。
然后最后一个小时回去调 T2。一开始没想到中间还能塞 \(1\),\(\text{40min}\) 后左右 \(O(n^3)\) 大样例终于过了,然后思考怎么优化,发现不会优化。因为怕错所以开始写数据点分治,写着写着只剩 \(\text{7min}\) 左右结束考试。拼尽全力想怎么优化,想了一个假的优化然后紧急撤回,最后检查文件遗憾离场。感觉卡满多测可能 \(O(n^3)\) 都拿不满,破防。多测数据范围何意味,\(\sum n\) 这么大给打部分分的选手是何居心。感觉 \(O(n^2)\) 都会被最后几个点卡,还要剪枝一下枚举。不敢估分,浮动范围挺大。
发现我要解决这样的问题:\(a\) 个可选 \(V=1/V=2\),\(b\) 个可选 \(V=0/V=1\)(\(V=0\) 是确定是 \(2\) 但是选不到的),要求这些 \(\sum V=sum\),求方案数。单独只有 \(a\) 时可以直接求出 \(1,2\) 的个数。可以对 \(b\) 个整体位移,变成 \(\sum V=sum+b\),然后就都变成 \(V=1/V=2\) 的问题,可以组合数后直接算出,做到 \(O(n^2)\)。
赛后 T2 通过代码(根据赛时改动)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=998244353;
const int N=5e3+5;
int n,m,a[N];
LL pw2[N],suf[N];
LL inv[N],fac[N],facinv[N];
void init(){
pw2[0]=1;
for(int i=1;i<=N-5;i++)
pw2[i]=pw2[i-1]*2%MOD;
inv[0]=inv[1]=1,
fac[0]=fac[1]=1,
facinv[0]=facinv[1]=1;
for(int i=2;i<=N-5;i++){
inv[i]=(MOD-MOD/i)*inv[MOD%i]%MOD;
fac[i]=fac[i-1]*i%MOD;
facinv[i]=facinv[i-1]*inv[i]%MOD;
}
}
inline LL C(int x,int y){return fac[x]*facinv[x-y]%MOD*facinv[y]%MOD;}
inline int FiND(int x){
int l=1,r=n+1,res=n+2;
while(l<=r){
int mid=(l+r)>>1;
if(a[mid]<x)res=mid,r=mid-1;
else l=mid+1;
}
return res;
}
inline LL get(int sum,int Len){
if(sum<0)return 0;
if(!Len&&!sum)return 1;
int cnt2=sum-Len;
if(cnt2<0||cnt2>Len)return 0;
return C(Len,cnt2);
}
int V[N],rk[N];
LL f[N*2];
inline bool cmp(int x,int y){
if(a[x]*V[y]!=a[y]*V[x])return a[x]*V[y]>a[y]*V[x];
else if(a[x]!=a[y])return a[x]>a[y];
return x<y;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
init();
int Cn,Tn;cin>>Cn>>Tn;
while(Tn--){
cin>>n>>m;suf[n+2]=0;suf[n+1]=1;
LL ans=0;
for(int i=1;i<=n;i++)
cin>>a[i];
a[n+1]=a[n+2]=0;
if(m==1){cout<<pw2[n]<<'\n';continue;}
sort(a+1,a+1+n,greater<int>());
for(int i=n;i>=1;i--)
suf[i]=(suf[i+1]+pw2[n-i])%MOD;
for(int x=1;x<n;x++){
int pos=n+1;
for(int y=x+1;y<=n;y++){
if(!(a[y]<a[x]&&a[x]<2*a[y]))continue;
int len=y-x-1;
while(pos>1&&a[pos-1]<a[x]-a[y])pos--;
LL ch1=get(m-2+len,x-1+len),ch2=suf[pos];
(ans+=ch1*ch2%MOD)%=MOD;
}
}
cout<<(pw2[n]-ans+MOD)%MOD<<'\n';
}
return 0;
}
在赛场上想,考完 S 后我还会认为自己是没发挥好,事实上是我的水平就是如此。实际上正赛和一般模拟赛的区别还是很大的,不会有显然的经典题和数据结构,会有题面阅读难度,会面对一些全新的 idea 和考点。这对于日常模拟赛来说是截然不同的一种体验,因此在训练 1 年水平稍微得到强化后,赛场能力还是显得薄弱。甚至可能为了某些题的正解,不如前几年以暴力拿分为主要目的的初二初三的我。
NOIP 2024 时曾许愿 2025 不留遗憾,现在看来挺难的了。考完意外地心里没什么波澜,像是打完了一场日常模拟赛,云无留迹就过去了。我的 OI 生涯是让自己成为渐行渐远的路人的一个漫长过程。凭借着过去自己的理想和现在自己的强烈目的性在燃烧,然后陨落。也许就应该这样吧,也许也应该这样吧。
Day 5
出分了,\(95+60+16+10=181\),意外地得到了一些没有预想的分数,还算是给自己这段时间的训练一个圆满的交代。
UPD:被卡 Luogu \(7\) 钩线了,气笑了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号