网络流学习笔记
网络流学习笔记
由于本人太菜了,至今不会网络流,写了篇很菜的学习笔记 qwq。
一些概念
网络:网络是指一种特殊的有向图 \(G=(V,E)\),存在容量和源汇点。
这里,我们记源点 \(s\),汇点 \(t\),边 \([u,v]\) 的容量为 \(c(u,v)\)。
可以想象一下,将有向图想象成一个庞大的水管系统,从一个端点倒水,水会从另外一个端点流出。
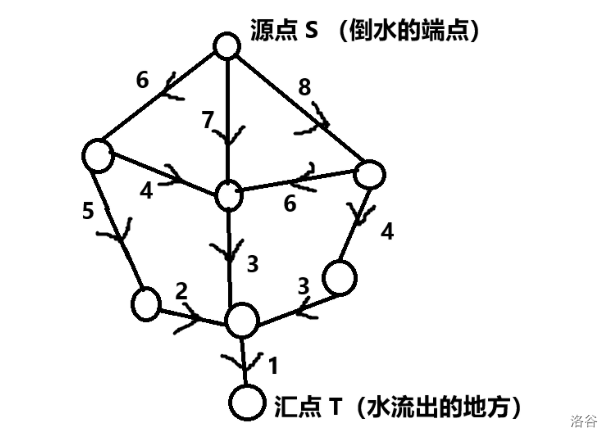
如图就是一张网络。(图丑勿喷)
流:对于一个网络 \(G=(V,E)\),流是一个从边集 \(E\) 的整数集或实数集的函数(记流函数 \(f(u,v)\)),满足:
1. 对于每条边,流经该边的流量不得超过该边的容量:\(0\leq f(u,v) \leq c(u,v)\)。
2. 除了 \(s,t\) 之外,任意节点 \(u\) 的净流量为 \(0\)。
这里同样可以想象,将水从源点倒入,显然只有汇点可以有水流出,其他的点都必须将流入的水全部排出到其他节点,这就是流守恒性。同时,水管中流的水不可以比容量大,这就是容量限制。
割:对于一个网络 \(G=(V,E)\),割是指将点集 \(V\) 分为两个集合 \(S\) 和 \(T\),其中源点 \(s \in S\),汇点 \(t \in T\)。割的容量定义为所有从 \(S\) 到 \(T\) 的边的容量之和。
形象地说,就是将网络中的一些水管直接切断,使得源点和汇点不再连通。切断的水管的容量之和就是割的容量。
以上的定义主要来自 oi-wiki,加上个人的理解。
常见问题
最大流问题:求从源点 \(S\) 到汇点 \(T\) 的最大流量。
最小割问题:找到一个割 \((S,T)\),使得割的容量最小。
费用流问题:每条边 \((u,v)\) 除了有容量 \(c(u,v)\) 之外,还有一个费用 \(cost(u,v)\),表示单位流量流经该边所需要的费用。在保证最大流的前提下,求最小(或最大)的总费用。
最大流
祭出洛谷模板题中的样例:
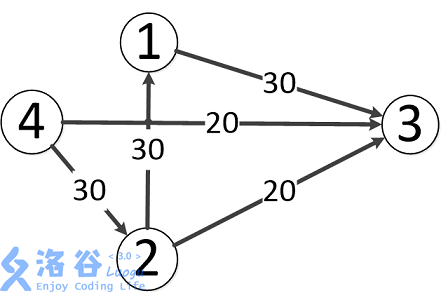
其中,\(s=4\),\(t=3\)。
不难算出,该网络中的最大流为 \(50\):
- \(4\to 2\to 3\),该路线可通过 \(20\) 的流量。
- \(4\to 3\),可通过 \(20\) 的流量。
- \(4\to 2\to 1\to 3\),可通过 \(10\) 的流量(边 \(4\to 2\) 之前已经耗费了 \(20\) 的流量)。
计算得 \(20+20+10=50\)。
不用上面自己的图是因为太难算了自己没算出来。
Edmonds-Karp 算法 (EK 算法)
在明白 EK 算法的实现过程之前,需要先了解:
增广路:在残留网络中,从源点 \(s\) 到汇点 \(t\) 的一条路径,其中路径上的所有边的剩余容量都大于 \(0\)。
简单来说,就是还没有被榨干的水管 /doge。
反向边:对于每条边 \((u,v)\),我们都建立一条反向边 \((v,u)\),容量为 \(0\)。当正向边 \((u,v)\) 的流量增加时,反向边 \((v,u)\) 的容量也增加,增加的值等于正向边增加的流量。
反向边的作用是:允许我们撤销之前的流量选择,从而找到更优的流量分配方案,具体在后面讲 EK 算法还会再说。
EK 算法是一种基于增广路的求解最大流的算法。它的核心思想是:每次寻找从源点到汇点的最短增广路,然后沿着增广路更新流量,直到找不到增广路为止。
算法步骤:
- 寻找增广路:使用 BFS 寻找从源点到汇点的最短增广路。
- 更新流量:沿着增广路更新流量,正向边减去流量,反向边加上流量。
- 重复步骤 1 和 2:直到找不到增广路为止。
时间复杂度:\(O(V \times E^2)\),其中 \(V\) 是顶点数,\(E\) 是边数。
实现代码
namespace EK{ //Edmonds-Karp算法求最大流
vector<int> pre;
vector<ll> dis;
bool BFS(){
vector<bool> vis(n+1,0);
queue<int> q;
q.push(s),vis[s]=1,dis[s]=INF;
while(!q.empty()){
int u=q.front();q.pop();
for(auto v:G[u]){
if(val_G[u][v]==0) continue; //找增广路只需要找残余网络中剩余容量大于0的边
if(vis[v]) continue; //如果结点已经访问过,就不再访问
dis[v]=min(dis[u],val_G[u][v]); //更新到达结点v的流量(求最小值)
pre[v]=u; //记录结点v的前驱结点,方便修改边权
q.push(v),vis[v]=1;
if(v==t) return 1; //如果可以从源点到达汇点,说明还存在增广路
}
}
return 0;//无法从源点到达汇点,说明不存在增广路
}
ll solve(){
dis.resize(n+1,0);
pre.resize(n+1,0);
ll res=0;
while(BFS()){
int x=t;
while(x!=s){
int v=pre[x]; //找到结点x的前驱结点
val_G[v][x]-=dis[t]; //正向边减去流量
val_G[x][v]+=dis[t]; //反向边加上流量
x=v;
}
res+=dis[t];
}
return res;
}
}
Dinic 算法
显然,EK 算法的时间复杂度是不够优秀的,每次都有可能遍历整个残量网络。
Dinic 算法是一种比 EK 算法更高效的最大流算法。通过分层图和多路增广提高效率。
算法步骤:
- 构造分层图:使用 BFS 构造从源点到各个顶点的分层图,记录每个顶点的层数。
- 多路增广:从源点开始,沿着分层图进行多路增广,每次尽可能地增加流量。
- 重复步骤 1 和 2:直到无法增广为止。
时间复杂度:\(O(V^2 E)\),对于某些特殊图可以达到 \(O(V^2 \sqrt{E})\)。
当前弧优化:在每次增广时,记录每个顶点已经访问过的边,下次增广时从上次访问的边开始继续访问,避免重复访问已经访问过的边。
实现代码
namespace Dinic{ //Dinic算法求最大流
vector<ll> pre,now,dis;
bool BFS(){
dis.assign(n+5,INF);
now.assign(n+5,0);
queue<int> q;
q.push(s),dis[s]=0;
now[s]=head[s];//当前弧优化
while(!q.empty()){ //BFS找到层次网络
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].val<=0||dis[v]!=INF) continue;
dis[v]=dis[x]+1; //更新层次
now[v]=head[v]; //更新当前弧
q.push(v);
if(v==t) return 1;
}
}
return 0;
}
ll DFS(int u,ll sum){ //DFS找到增广路
if(u==t)return sum;
ll k,res=0;
for(int i=now[u];i&∑i=e[i].nxt){
now[u]=i;
int v=e[i].to;
if(e[i].val<=0||(dis[v]!=dis[u]+1))continue;
k=DFS(v,min(sum,e[i].val)); //找到增广路上的最小流量
if(k==0)dis[v]=INF;
e[i].val-=k,e[i^1].val+=k; //正向边减去流量,反向边加上流量
res+=k,sum-=k;
}
return res;
}
ll solve(){
pre.assign(n+5,0);
now.assign(n+5,0);
ll res=0;
while(BFS()){ //每次找到一条增广路,就更新一次层次网络
res+=DFS(s,INF); //每次找到一条增广路,就更新最大流
}
return res;
}
}
最小割
最大流最小割定理: 对于任意网络,最大流的值等于最小割的容量。
证明可以参照 oi-wiki。
根据定理,求出一个网络的最大流就可以求出该网络的最小割的容量。
费用流
在求最大流的同时添加了每条边的费用,使费用最小。
EK+SPFA 求费用流
EK 求最大流的过程就是通过 BFS 不断寻找增广路,每次找到一条之后更新,通过反向边进行反悔。
现在加入了费用的概念,不难联想到最短路算法。
此时会有一个大胆的想法:SPFA 和 Dij 都是基于 BFS 进行的,那么是不是只需要把 EK 中的 BFS 替换成 SPFA/Dij 就行了呢?
而前文提到求最大流一个很重要的步骤就是建立反向边反悔,而一条正向边的费用显然大于 \(0\),而反向边为了能够正确地进行反悔,其费用就需要取正向边的相反数。
于是这个网络出现了负边,Dij 死倒闭了。
那为什么把 BFS 换成 SPFA 求最小费用最大流就是对的呢?
-
如果两条边的流量相同,我们需要找到费用较小的那一条边,这一部分 SPFA 显然是对的。
-
如果流量较大的那条边费用较小,用最短路算法找增广路就一定会找到这条边,可以保证流量最大且费用最小。
-
如果流量较大的那条边费用较大,用最短路算法第一遍会找到费用较小的那条边,于是流量大的边成为了图中的一条增广路。按照 EK 的求解步骤,流量较大的边还是会被找到并更新。
因此就可以用 EK+SPFA 求最小费用最大流了!
实现代码
namespace EK{ //EK+SPFA求最大流最小费用
vector<ll> dis,F;
vector<int> pre,vis;
bool SPFA(){
dis.assign(n+1,INF),F.assign(n+1,INF);
pre.assign(n+1,0),vis.assign(n+1,0);
queue<int> q;
q.push(s);
dis[s]=0,vis[s]=1,F[s]=INF;
while(q.size()){
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].w&&dis[v]>dis[u]+e[i].c){
dis[v]=dis[u]+e[i].c;
F[v]=min(F[u],e[i].w);
pre[v]=i;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
return dis[t]!=INF;
}
pair<ll,ll> solve(){
ll max_flow=0,cost=0;
while(SPFA()){
for(int i=t;i!=s;i=e[pre[i]^1].to){
e[pre[i]].w-=F[t];
e[pre[i]^1].w+=F[t];
}
max_flow+=F[t];
cost+=dis[t]*F[t];
}
return {max_flow,cost};
}
}
网络流建图技巧例题
P1646 [国家集训队] happiness
模型:二元关系最小割模型
题目大意
有一个 \(n\times m\) 的同学矩阵,现在要分文理科,每个同学对于选择文科与理科有着自己的喜悦值。
而一对好朋友如果能同时选文科或者理科,那么他们又将收获一些喜悦值。
求最大喜悦总和。
解题思路
考虑每个同学必须选择文科/理科(废话),容易想到对这个矩阵建网络求最小割。
先建立一个源点 \(s\) 和一个汇点 \(t\),每个同学都建一个点,共 \(n \times m + 2\) 个点。
对于第一种关系:同学选文科 or 理科的喜悦值,分别将该同学节点向 \(s\) 或 \(t\) 建边。
对于第二种关系:两个相邻的同学同选文科 or 理科的喜悦值,直接将这两个同学之间建边。
边权要怎么定?
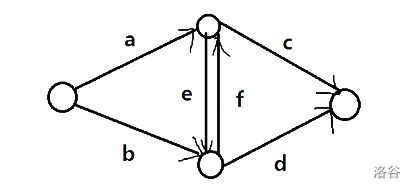
参照这张图,我们解方程。
首先令第 \(i\) 位同学选文科的喜悦值为 \(A_i\);第 \(i\) 位同学选理科的喜悦值为 \(B_i\);
第 \(i\) 和 \(j\) 位同学同选文科喜悦值为 \(C_{i,j}\);第 \(i\) 和第 \(j\) 位同学同选理科的喜悦值为 \(D_{i,j}\)。
然后对于每个点对 \((i,j)\) 列出方程:(按照同文、同理、一文一理、一理一文的顺序)。
\( \begin{cases} c + d = B_i + B_i + D_{i,j} \ \ \ \ (1) \\ a + b = A_j + A_j + C_{i,j} \ \ \ \ (2) \\ b + c + e = B_i + A_j + C_{i,j} + D_{i,j} \ \ \ \ (3) \\ a + d + f = A_i + B_j + C_{i,j} + D_{i,j} \ \ \ \ (4) \\ \end{cases} \)
理解一下,这些边的贡献等于割掉这些边后会失去的贡献。
解方程:\((3)+(4)-(1)-(2)\) 得到 \(e+f=C_{i,j}+D_{i,j}\)。
\(e=f\),所以 \(e=f=\frac{C_{i,j}+D_{i,j}}{2}\)
由于方程的解需要对称,注意到当 \(a=A_i+\frac {c_{i,j}}{2}\) 时,解得:
\( \begin{cases} a = A_i+\frac {c_{i,j}}{2} , b = A_j+\frac {c_{i,j}}{2} \\ \\ c = B_i+\frac {d_{i,j}}{2} , d = B_j+\frac {d_{i,j}}{2}\\ \end{cases} \)
根据这个方程建边,跑 Dinic 求出最小割,最后用总和减去最小割容量就是答案。
P4043 [AHOI2014/JSOI2014] 支线剧情
模型:有源汇有上下界最小费用流
题目大意
一个点游戏中从起始剧情点 \(1\) 开始,所有剧情点都是从 \(1\) 号可达,并且无法回到已经经过的剧情点。
每条边(支线剧情都有一个时间花费)都代表了一段剧情过渡。
由于游戏剧情不可逆,且无法回退,只能退出后重新从1开始,所以需要规划若干次游戏过程(路径),使得最终能够观看到所有的支线剧情,同时使得所有路径的总时间最小。
解题思路
将原问题转化为一个上下界的最小费用流问题。
由于所有边都至少要遍历一遍,所以先固定地把这条边计入答案,同时维护顶点的度数变化。
对于每条原始边,从 \(i\) 到 \(v\) 加一条无限容量、费用 \(w\) 的边。
为了保证所有点都能连通源点,额外添加从所有点到 \(1\) 号(源点)的边(容量无限,费用 \(0\))。
同时对于每个点:
- 如果 \(d_i\) 大于 \(0\)(流入较多),从源点 \(s\) 到 \(i\) 加边;
- 如果 \(d_i\) 小于 \(0\)(流出较多),从 \(i\) 到汇点 \(t\) 加边。
为了使流环路收敛,构造一条从 \(t\) 到 \(s\) 的边(无限容量、费用 \(0\)),实际上是构成了一个流的循环结构。
EK + SPFA 求出最小总费用,将这个最小费用加到先计算的 ans 上就是最终的最小总时间。
P2766 最长不下降子序列问题
题目来源:网络流与线性规划24题
模型:最多不相交路径
题目大意
- 求最长的不下降子序列的长度 \(s\)(子序列中元素按照原序列的顺序且允许相等)。
- 在每个元素只能使用一次的条件下,求最多可以选出多少个长度为 \(s\) 的不下降子序列(同一元素最多出现在一个子序列中)。
- 允许序列中的首元素 \(x_1\) 和末元素 \(x_n\) 可重复使用(其他元素仍只能用一次)的情况下,求最多能取出多少个不同的长度为 \(s\) 的不下降子序列,其中两个子序列的下标序列不同即认为不同。
解题思路
第一问是一个简单 dp,计算求解完之后将求得的答案和 f 数组保留,后面两问要用到。
第二问:
注意到 \(a_j\) 加 \(a_i\) 可以构成一个不下降子序列,当且仅当 \(j \le i\),\(a_j \leq a_i\)。
开始建图:定义源点 \(s=0\),汇点 \(t=2\times n +1\)。
将每个点拆成两个点,\(i\) 向 \(i+n\) 连边,容量为 \(1\)。
如果 \(f_i=1\),则 \(s\) 向 \(i\) 连边,容量为 \(1\)。
如果 \(f_i=max_LIS\),则 \(i+n\) 向 \(t\) 连边,容量为 \(1\)。
跑一边最大流就是答案。
第三问:
和第二问类似,只需要把 \(1\) 和 \(n\) 相关的边的容量改为 INF 即可。
最后还需要判断一下一种特殊情况:
如果序列严格递减,对于每个 \(i\) 都有 \(f_i=1\),恰好 \(s=1\)。
这个时候由于我们的建图策略,\(s\) 到 \(i\) 有一条 INF 的边,\(i\) 到 \(i+n\) 有一条 INF 的边,\(i+n\) 到 \(t\) 有一条 INF 的边。
此时最大流为 INF(雾。
但是我们知道,答案应该是 \(n\),特判一下就好了。
看完这些例题,像我这样的萌新肯定会产生疑惑:这些鬼魅的建图为什么都是对的?
这个时候建议手模一下这个建图,自己算一下样例,你就会发现其精妙所在。
虽然有可能证明不出来,但是差不多也能理解其正确性了。
那像我这样的萌新还是会产生疑惑:这些绝妙思路怎么才能自己想出来呢?
建议大家可以再看一下 这篇博客。
里面总结了各种网络流的建图技巧和模型以及分别的例题,属于史诗级巨作。
聪明的你,如果可以把里面每一个模型都理解透彻,那你就可以成为网络流大神了!
后面我可能还会再做一些不同模型的例题qwq。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号