141. [链表][双指针][哈希表]环形链表

141. 环形链表

方法一：哈希表

最容易想到的方法是遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过。

具体地，我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。重复这一过程，直到我们遍历完整个链表即可。

public class Solution {
    public boolean hasCycle(ListNode head) {
        HashSet<ListNode> seen = new HashSet<>();
        while(head != null){
            if(seen.contains(head)){
               return true;
            }
            seen.add(head);
            head = head.next;
        }
        return false;
    }
}

从这个方法中我衍生了一些思考，为什么ListNode可以作为HashSet的泛型？自定义的一个 \(Object\) 可以计算 hashCode吗？

在 java.lang.Object中可以看到：

public class Object {
    // ...
    // Indicates whether some other object is "equal to" this one.
    public native int hashCode();
    // ...
}

可以看出，自定义 Object 确实是可以计算 hashCode的，这保证了我们的自定义类可以作为HashSet的key。

native关键字是Java与C/C++联合开发的时候用的。使用native关键字说明这个方法是原生函数，也就是这个方法是用C/C++语言实现的，并且被编译成了DLL，由Java去调用。这些函数的实现体在DLL中，JDK的源代码中并不包含，你应该是看不到的。对于不同的平台它们也是不同的。这也是Java的底层机制，实际上Java就是在不同的平台上调用不同的native方法实现对操作系统的访问的。

总结一下，Java是跨平台的语言，既然是跨了平台，所付出的代价就是牺牲一些对底层的控制，而Java要实现对底层的控制，就需要一些其他语言的帮助，这个就是native的作用了 。

方法二：快慢指针

public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head == null || head.next == null){
            return false;
        }
        ListNode slow = head, fast = head.next;
        while(slow != fast){
            // 只要快指针先变得到null，说明肯定不存在环
            if(fast == null || fast.next == null){
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}

补充知识：

Floyd 判圈算法 (Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法 (Tortoise and Hare Algorithm)。该算法由美国科学家罗伯特·弗洛伊德发明，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

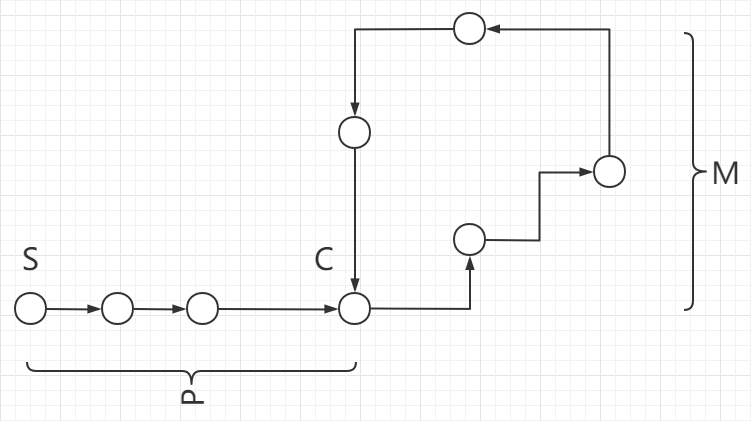
初始状态下，假设已知某个起点节点为节点S。现设两个指针slow 与 fast，将它们均指向S。

接着，同时让slow 与 fast往前推进，但是二者的速度不同：slow 每前进1步，fast前进2步。只要二者都可以前进而且没有相遇，就如此保持二者的推进。当fast无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。反之当slow 与 fast再次相遇时，就可以确定从S出发一定会进入某个环，设其为环M。

如果确定了存在某个环，就可以求此环的起点与长度。

计算环的长度

上述算法刚判断出存在环M时，显然slow 与 fast位于同一节点，设其为节点T1。显然，仅需令fast不动，而slow不断推进，最终又会返回节点T1，统计这一次slow推进的步数，显然这就是环M的长度。

计算环的起点

为了求出环M的起点，只要令fast仍位于节点T1，而令slow返回起点节点S。随后，同时让slow 与 fast往前推进，且保持二者的速度相同：slow 每前进1步，fast前进1步。持续该过程直至slow 与 fast再一次相遇，设此次相遇时位于同一节点T2，则节点T2即为从节点S出发所到达的环M的第一个节点，即环M的一个起点。

链表起点为节点S，环起点为节点T2，slow 与 fast相遇时位于同一节点T1，设节点S和节点T2之间的距离为\(p\)，节点T2和节点T1之间的距离为\(m\)，环长为\(c\)，这里两点之间的距离是指从一点走多少步可以到点另外一点。

当slow 与 fast相遇时：

• slow走的步数，\(step = p + m + a * c\)，a表示相遇时slow走的圈数
• fast走的步数，\(2 * step = p + m + b * c\)，b表示相遇时fast走的圈数

两者相减：\(step = (b - a) * c = p + m + a * c\)，由此可知t走的步数是环M的倍数，即 p + m 刚好是环长度 \(c\) 的倍数。

slow 与 fast在T1处相遇，为了计算环M的起点，令fast仍位于节点M，而令slow返回起点S，随后，同时让slow 与 fast往前推进，且保持两者的速度相同：slow每前进1步，fast前进1步。持续该过程直至slow 与 fast再一次相遇，则它们此次相遇时一定位于环的起始节点T2。为什么它们此次相遇时一定在环起始节点呢？

slow走了\(p\)步到达P，fast在环M上\(p\)步在哪呢？fast从T1处出发走了\(p\)步，相对于环起始位置，slow走过的距离是 \(m + p\)，而\(m + p\)刚好是环长度\(c\)的倍数，即fast此时也位于环起始节点处，即slow 与 fast在T2处相遇。据此就可以计算出环起始节点的位置。
------------恢复内容结束------------