二分查找详解

二分查找算法

引言

当我们要在一个有序的数据序列里面查找一个数据的时候，我们所能想到的最简单的方法就是简单遍历。
我们假设数据大小是 n，那么简单遍历的最好情况是1次比较就找到目标值，而最坏的情况是比较n次。算法时间复杂度为O（n）

数据量小的时候简单遍历查找是可行的，而当数据很大的时候，这个过程会变得非常缓慢。

简单查找逐个地检查数字，如果列表包含100个数字，最多需要猜100次。如果列表包含40亿个数字，最多需要猜40亿次。换言之，最多需要猜测的次数与列表长度相同，这被称为线性时间（linear time）。

二分查找则不同。如果列表包含100个元素，最多要猜7次；如果列表包含40亿个数字，最多需猜32次。厉害吧？二分查找的运行时间为对数时间（或log时间），下表总结了我们发现的情况。

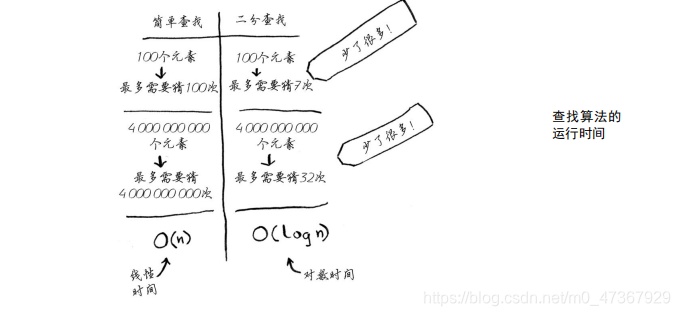
那么这个差距到底有多夸张呢？让我们看看下面这个例子：

Bob要为NASA编写一个查找算法，这个算法在火箭即将登陆月球前开始执行，帮助计算着陆地点。

这个示例表明，两种算法的运行时间呈现不同的增速。
Bob需要做出决定，是使用简单查找还是二分查找。使用的算法必须快速而准确。一方面，二分查找的速度更快。Bob必须在10秒钟内找出着陆地点，否
则火箭将偏离方向。另一方面，简单查找算法编写起来更容易，因此出现bug的可能性更小。Bob可不希望引导火箭着陆的代码中有bug！为确保万无一失，Bob决定计算两种算法在列表包含100个元素的情况下需要的时间。

假设检查一个元素需要1毫秒。使用简单查找时，Bob必须检查100个元素，因此需要100毫秒
才能查找完毕。而使用二分查找时，只需检查7个元素（log2100大约为7），因此需要7毫秒就能查
找完毕。然而，实际要查找的列表可能包含10亿个元素，在这种情况下，简单查找需要多长时间
呢？二分查找又需要多长时间呢？请务必找出这两个问题的答案，再接着往下读

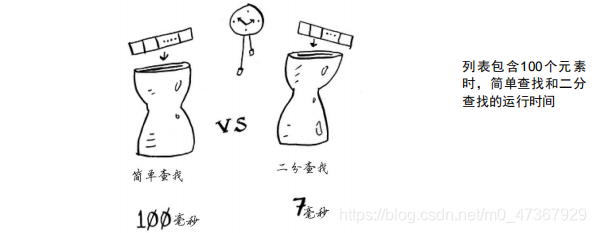
Bob使用包含10亿个元素的列表运行二分查找，运行时间为30毫秒（log21 000 000 000大约为30）。他心里想，二分查找的速度大约为简单查找的15倍，因为列表包含100个元素时，简单查找需要100毫秒，而二分查找需要7毫秒。因此，列表包含10亿个元素时，简单查找需要30 × 15 = 450毫秒，完全符合在10秒内查找完毕的要求。Bob决定使用简单查找。这是正确的选择吗？
不是。实际上，Bob错了，而且错得离谱。列表包含10亿个元素时，简单查找需要10亿毫秒，相当于11天！为什么会这样呢？因为二分查找和简单查找的运行时间的增速不同

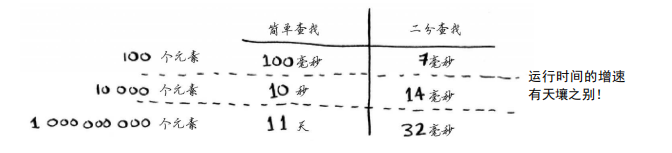
也就是说，随着元素数量的增加，二分查找需要的额外时间并不多，而简单查找需要的额外时间却很多。因此，随着列表的增长，二分查找的速度比简单查找快得多。Bob以为二分查找速度为简单查找的15倍，这不对：列表包含10亿个元素时，为3300万倍。

大O表示法

所以我们不能这样比较估计两个算法的运行时间，因为它并不是简单的倍数关系。所以我们引入大O表示法来表示算法的时间复杂度，估计算法的上界。

大O表示法指出了算法有多快。例如，假设列表包含n个元素。简单查找需要检查每个元素，因此需要执行n次操作。使用大O表示法，
这个运行时间为O(n)。

单位是秒吗？并不是的——大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

再来看一个例子。为检查长度为n的列表，二分查找需要执行log n次操作。使用大O表示法，这个运行时间怎么表示呢？O(log n)。一般而言，大O表示法像下面这样。

二分查找的实现过程图解

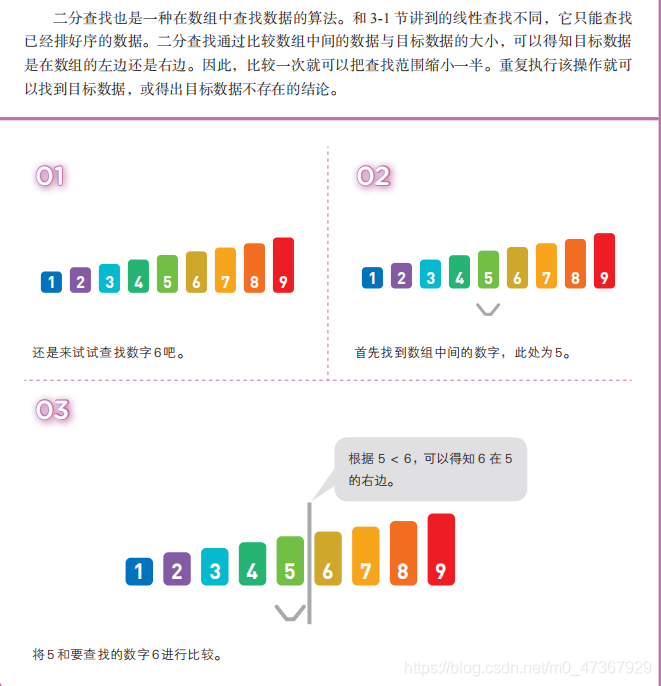
解说

二分查找利用已排好序的数组，每一次查找都可以将查找范围减半。查找范围内只剩一个数据时查找结束。数据量为 n 的数组，将其长度减半 log2n 次后，其中便只剩一个数据了。也就是说，在二分查找中重复执行“将目标数据和数组中间的数据进行比较后将查找范围减半”的操作 log2n 次后，就能找到目标数据（若没找到则可以得出数据不存在的结论），因此它的时间复杂度为 O(logn)。

二分查找算法的递归和非递归代码实现

//非递归
int SearchBan(int A[],int key)//数组参数，和目标值参数
{
    int low=1 ,high=ST.length,mid;
    while(low<=high)
    {
        mid=(low+high)/2;
        if(key==A[mid])
        {
            return mid;
        }
        else if(key<A[mid])
        {
            high=mid-1;
        }
        else low=mid+1;
    }
    return 0;

}

//递归实现
int SearchBan(int A[],int low,int high,int key)//数组参数，和目标值参数
{
        mid=(low+high)/2;
        if(key==A[mid])
        {
            return mid;
        }
        else if(key<A[mid])
        {
           return SearchBan(A,low,mid-1,key);
        }
        else return SearchBan(A,mid+1,high,key);
    return 0;

}

二分查找算法的局限性

• 二分查找法依赖的是顺序表结构，简单点来说就是数组。主要原因是二分查找方法需要按照下标随机访问元素。如果使用其他数据结构，时间复杂度就会提高。
• 二分查找针对的是有序数据。所以二分查找只能在插入、删除操作不频繁，一次排序多次查找的场景中。
• 数据量太小不适合二分查找，如果要处理的数据量很小，顺序遍历就够了。不过，如果元素直接的比较操作非常耗时，例如字符串之间的比较，不管数据量大小，都推荐使用二分查找算法。
• 数据量太大也不适合用二分查找，因为二分查找依赖于顺序存储结构，要求内存空间连续，如果数据量很大的情况下，可能存在空间不够分配的困难。