0-1背包问题详解

引言

小偷问题：

假设你是个贪婪的小偷，背着可装4磅（1磅≈0.45千克）重东西的
背包，在商场伺机盗窃各种可装入背包的商品。你力图往背包中装入价值最高的商品，你会使用哪种算法呢？同样，你采取贪心策略，这非常简单。
(1) 盗窃可装入背包的最贵商品。
(2) 再盗窃还可装入背包的最贵商品，以此类推。
只是这次这种贪心策略不好使了！例如，你可盗窃的商品有下面三种。

如果用贪心法，那么先把价值最高的音响放进去，这样直接背包容量就满了，那么贪心出来的最高价值就是3000美元，可是这样做真的是最优解吗？显然不是的，吉他+笔记本电脑总价值为3500，而且容量也没有超出，这才是最优解，说明这个时候贪心的方法不再适用了。

动态规划

那么我们开始介绍新的解决这类问题的方法，这就是动态规划。
动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。

• 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
• 与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，.进行进一步的求解)
• 动态规划可以通过填表的方式来逐步推进，得到最优解。
  
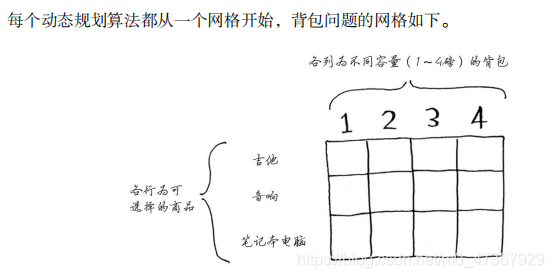
  网格的各行为商品，各列为不同容量（1～4磅）的背包。所有这些列你都需要，因为它们将帮助你计算子背包的价值。网格最初是空的。你将填充其中的每个单元格，网格填满后，就找到了问题的答案！你一定要跟着做。请你创建网格，我们一起来填满它。

1. 吉他行
   意味着你将尝试将吉他装入背包。在每个单元格，都需要做一个简单的决定：偷不偷吉他？别忘了，你要找出一个价值最高的商品集合。
   第一个单元格表示背包的容量为1磅。吉他的重量也是1磅，这意味着它能装入背包！因此这个单元格包含吉他，价值为1500美元。下面来开始填充网格。
   
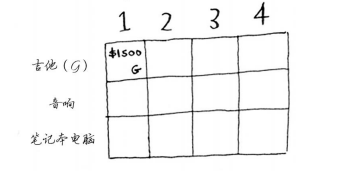
   吉他重量为1磅，所以后面的容量装下吉他是肯定够的，所以把吉他价值1500填入表格中。
   
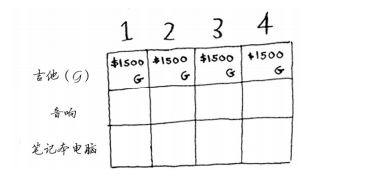
   此时你很可能心存疑惑：原来的问题说的是4磅的背包，我们为何要考虑容量为1磅、2磅等的背包呢？前面说过，动态规划从小问题着手，逐步解决大问题。这里解决的子问题将帮助你解决大问题。请接着往下读，稍后你就会明白的。

2. 音响行
   我们来填充下一行——音响行。你现在出于第二行，可偷的商品有吉他和音响。在每一行，可偷的商品都为当前行的商品以及之前各行的商品。因此，当前你还不能偷笔记本电脑，而只能偷音响和吉他。我们先来看第一个单元格，它表示容量为1磅的背包。在此之前，可装入1磅背包的商品的最大价值为1500美元。
   
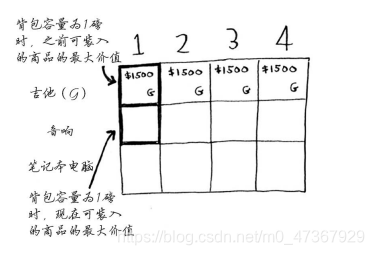
   该不该偷音响呢？
   背包的容量为1磅，能装下音响吗？音响太重了，装不下！由于容量1磅的背包装不下音响，因此最大价值依然是1500美元。

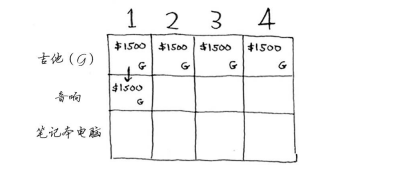
接下来的两个单元格的情况与此相同。在这些单元格中，背包的容量分别为2磅和3磅，而以前的最大价值为1500美元。
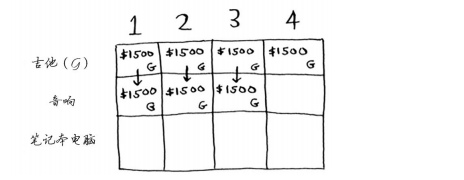由于这些背包装不下音响，因此最大价值保持不变。背包容量为4磅呢？终于能够装下音响了！原来的最大价值为1500美元，但如果在背包中装入音响而不是吉他，价值将为3000美元！因此还是偷音响吧。

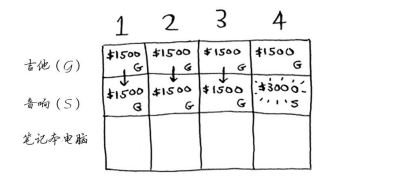
你更新了最大价值！如果背包的容量为4磅，就能装入价值至少3000美元的商品。在这个网格中，你逐步地更新最大价值。

3.笔记本电脑行
下面以同样的方式处理笔记本电脑。笔记本电脑重3磅，没法将其装入容量为1磅或2磅的背包，因此前两个单元格的最大价值还是1500美元。

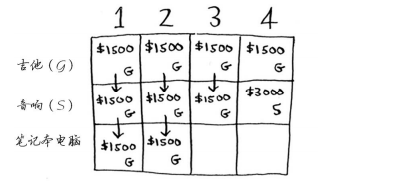
对于容量为3磅的背包，原来的最大价值为1500美元，但现在你可选择盗窃价值2000美元的笔记本电脑而不是吉他，这样新的最大价值将为2000美元！

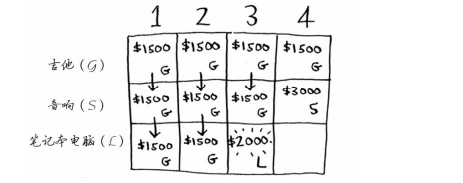
对于容量为4磅的背包，情况很有趣。这是非常重要的部分。当前的最大价值为3000美元，你可不偷音响，而偷笔记本电脑，但它只值2000美元。

根据之前计算的最大价值可知，在1磅的容量中可装入吉他，价值1500美元。因此，你需要做如下比较。

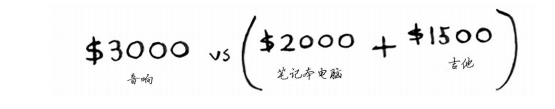
你可能始终心存疑惑：为何计算小背包可装入的商品的最大价值呢？但愿你现在明白了其中的原因！余下了空间时，你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元，因此偷它们是更好的选择。

最终的网格类似于下面这样：

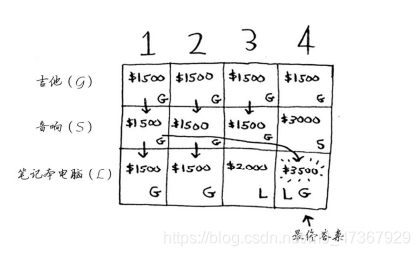
答案如下：将吉他和笔记本电脑装入背包时价值最高，为3500美元。你可能认为，计算最后一个单元格的价值时，我使用了不同的公式。那是因为填充之前的单元格时，我故意避开了一些复杂的因素。其实，计算每个单元格的价值时，使用的公式都相同。这个公式如下：

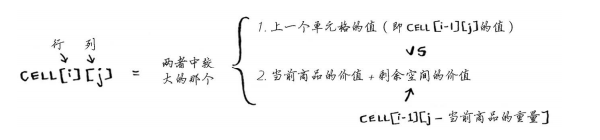
你可以使用这个公式来计算每个单元格的价值，最终的网格将与前一个网格相同。现在你明白了为何要求解子问题吧？你可以合并两个子问题的解来得到更大问题的解。

思路已经了解了，来试试你能不能把代码写出来吧！，当然我在后面贴出了实现代码，不过还是要自己先写写，遇到问题可以再回来参考啊。

代码实现

#include <iostream>

#define MaxN 20
using namespace std;
int w[MaxN]={0,1,3,4};
int v[MaxN]={0,1500,2000,3500};
int dp[MaxN+1][MaxN+1];
int n=3,c=4;
int x[MaxN];
int maxv;
void knapsack()
{
    for(int i= 1;i<=n;i++)
    {
        dp[0][i]=0;
    }
     for(int i= 1;i<=n;i++)
    {
        dp[i][0]=0;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=c;j++)
        {
            if(j<=w[i])
            {
                dp[i][j]=dp[i-1][j];
            }
            else{
               dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
            }
        }
    }
}
int main()
{
    knapsack();
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=c;j++)
        {
            printf("%6d",dp[i][j]);
        }
        printf("\n");
    }
    return 0;
}