6.1 常用程序结构模式 - 可重入 VI 和递归算法
重入执行是子 VI 的一个属性。默认情况下,VI 是不会被设置这个属性的;需要设置它时,可以在 VI 属性对话框中,选中 "重入执行" 选项。设置了这一属性的 VI,称为可重入 VI。
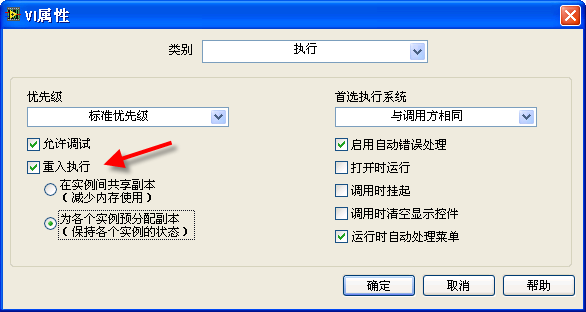
子 VI 被设置为可重入,那么在程序的不同地方调用这个子 VI 时,它会在内存中为每一处的调用各生成一个新的 VI 实例
为各个实例预分配副本" 表示每处调用生成的实例 VI 都拥有各自独立的数据区,数据互不干扰
"在实例间共享副本" 是 LabVIEW 8.5 之后出现的选项,它是指这些实例 VI 使用同一块数据区。
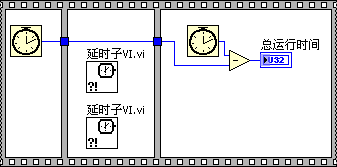
如果延时子 VI 是非可重入的,则由于两处调用只能先后分别运行,程序总运行时间为 2 秒。若延时子 VI 是可重入的,则两处调用可以同时运行,程序总运行时间为 1 秒。
递归算法
递归是指一个 VI 直接调用自身,或者间接调用自身,比如:VI_1 调用 VI_2,VI_2 又调用 VI_1
递归的策略是把一个大的复杂的问题转换为一个小的和原问题相似的问题,再进一步把问题拆成更小的问题,最终解决整个问题。
理论上,任何需要使用递归调用的地方,都可以用循环结构来代替。
计算阶乘
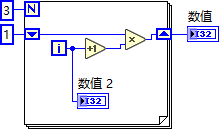
调用自身VI( VI 的可重入属性设置为 "让各个实例间共享空间" )
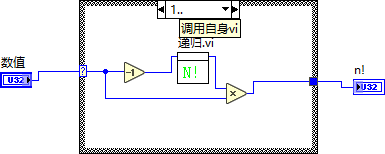
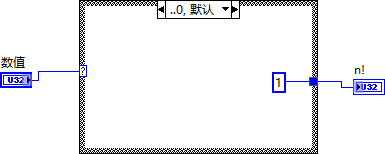
计算斐波纳契数列
F (0)=0F (1)=1F (n)=F (n-1) + F (n-2) |(n≧2)
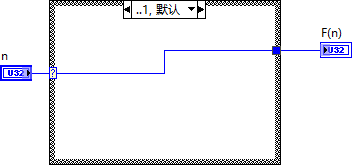
当输入 n 大于等于 2 时,VI 调用自身两次,一次输入 n-1,另一次输入 n-2;然后把两个子 VI 输出的结果相加,输出结果
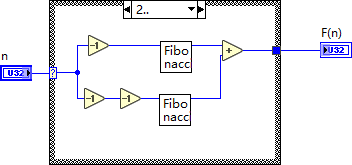
另一个提高效率的思路是:保证每计算一个步,只递归调用本身一次,这样也可以避免重复计算。
这个思路来编写程序,程序有两个输入 a 和 b 分别记录前两次的运算结果(没看懂)。
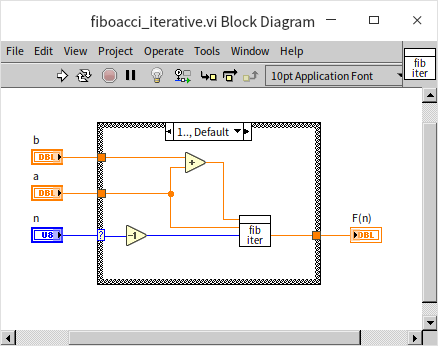
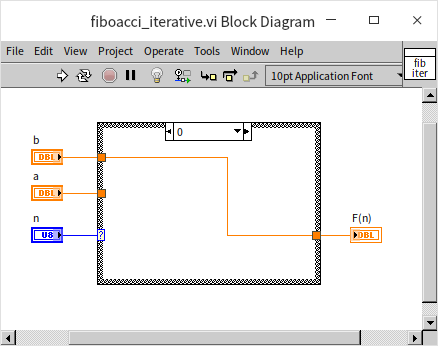
带缓存的递归
缓存可以使用任何数据结构来构建。计算斐波纳契数列时需要针对从 0 开始的每一个整数进行计算,所以非常适合使用数组来做缓存
很多时候,递归算法的输入数据并不是连续的整数,一个更通用的缓存设计是使用 Map 数据结构。Map 中文的直接翻译是“映射”,
很多类似的名词比如:关联数组、字典、散列表、查找树等,它们所指的都是一类接口相似的数据结构,在结构中保存的每条数据是由一个“键”和一个“值”组成的一对数据。使用者可以在结构中,使用“键”来快速查找到“值”。在使用 Map 做缓存时,可以使用程序的输入数据作为“键”,程序的运行结果作为“值”。
添加了缓存的计算斐波纳契数的程序框图
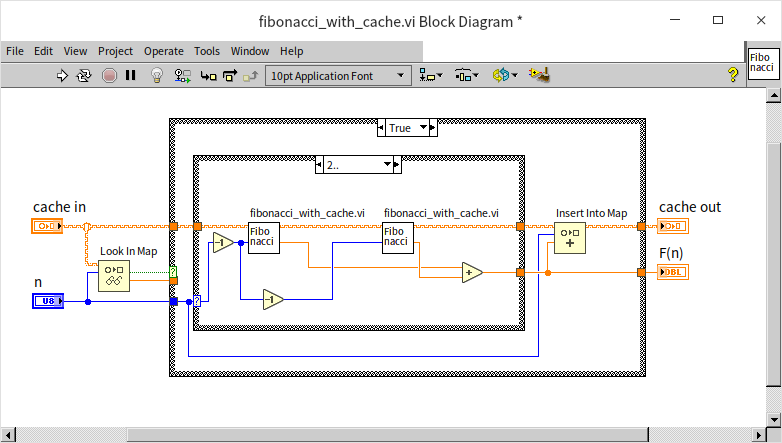
编写递归程序的步骤
- 明确一个递归结束的条件,也就是归纳法的基本情况。如果递归调用的结束条件设置不当,可能会引起程序死循环甚至崩溃。
- VI 中先放置一个条件结构,检查当前输入是否满足递归结束条件。如果满足返回基础条件设定的结果。
- 输入值若不满足递归结束条件,则想办法把问题拆分成可以用更小或更简单的相似问题,然后使用更小或更简单的输入调用算法 VI 自身,得到子问题的结果。
- 对子问题的结果进行归并处理,得到当前问题的结果。
- 没有递归编程经验可能会比较难以理解程序代码。
- 任何需要使用递归算法的地方,都可以用循环来代替。递归算法的运行效率通常低于循环算法。
- 参与递归调用的 VI 必须被设置为 "让各个实例间共享空间" (Shared clone reentrant execution) 的可重入 VI。这一设置在 VI 属性对话框的 "执行" 页面:
普通 VI 为什么不能被递归调用
不能把一个 VI 当作自身的子 VI。(普通 VI(非可重入的 VI))
VI 每次被调用的时候都从同一片数据区读取数据,这是处于效率的考虑。因为这个设置,在每一个时间,同一个子 VI 只能被运行一次。因为 LabVIEW 需要借此来保证多线程时的数据安全。
关于多线程和内存管理的问题,本书会在 LabVIEW 的运行机制 和 多线程编程 章节内做更详细讨论。
LabVIEW 在静态调用 “为每个实例预分配空间” 的可重入子 VI 时,把数据区设置在了调用它的父 VI 中。也就是说,子 VI 的数据区是在程序运行前,就开辟好了的。
而在递归调用时,是无法在程序运行前就确定子 VI 要被调用多少次的,调用次数是动态的,LabVIEW 无法知道需要为它准备多少个独立的数据区,所以也就不可以静态递归调用。(让各个实例间共享空间总的来说,如果起名为 “动态分配空间” 可能会更好理解一些。)
练习
- 编写一个 VI 使用递归算法计算列出输入数组的全排列。比如,输入的数组是[1, 2, 3],输出一个二维数组,每一行代表这三个输入数据的一种排列方式: [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号