什么是图数据上的规则

规则

图规则并不是深入研究图论，图规则的相关工作更像是数据库领域的一个分支。

规则的诞生和使用最早是应用在数据库领域中，比如创建表时使用的‘完整性约束’，为了说明插入该表中的数据必须满足一定的约束（某个属性非空等等）；此外，规则也被广泛的应用在数据挖掘等领域中。关系型数据库应用广泛，很多关于规则的研究也集中在关系型数据库中。在关系型数据库中，规则有一个更加形式化的定义：R(X->Y)。R代表一张表，X和Y都是可以看作是两个集合，其中的元素是要做出真假判断的‘谓词’。
假如一张表的schema是 R(id,name,age,city)，t1和t2是R中的两条数据，X中包含的谓词有 t1.id=t2.id,t1.name=t2.name; Y中包含的谓词有t1.age=t2.age,t1.city=t2.city。 这就是一条能够判断R的数据之间age和city关系的规则，利用规则可以做数据库上的重复数据查找，补充缺失数据等等。

类似于上述关系型数据库的规则，图规则是作用在图数据上的规则。但是呢，相比于关系型数据库上的规则的广泛使用（这是可以写到数据库教材里面的内容），图数据上关于规则的研究则刚刚兴起。
相比于关系型数据模型，图数据之间拥有更加直接和广泛的联系，这更加符合真实世界中事物之间的关系。

图数据的定义

类似于数据结构中的图，这里使用的图的定义是一个四元组 G = {E,V,L,F}: E和V分别代表节点和边（不失一般性，这里只考虑有向图）；L表示节点和边的label；F则是节点上的attributes。关于label和attribute，我觉得label更像是在描述节点之间的关系，比如人物关系图中两个节点 a,b。如果a是b长辈，那么a指向b的边就可以用label来表示这种关系。 attribute则更像是数据库中的数据，只存在于节点上，类似于关系型数据库中的属性。但是和关系型数据不同的是，图数据并没有一个schema，因此，不同的节点可能有不同的attributes，这样也导致关系型数据和图数据上的规则的语义的不同。

可以想见，在图数据上使用规则，一方面是要找到施用规则的节点，另一方面，则是要将规则中的值的约束体现出来。

图规则

图规则是图的拓扑关系和节点之间属性值关系的结合。

图模式 （Graph Pattern）和图匹配（Graph Matching）

Graph Pattern是为了确定图数据的节点，它的定义类似于子图。
关于图Q的Patter定义如下： Q[x] = (V',E',L),V'和E'分别是Pattern中的节点和边，L则表示V'和E'中每个节点和边的label。关于Pattern中的label，这里有一个通配符，让'_'表示一个能够和任意label匹配的label，x是一个向量，是代表节点的变量。
Pattern相对于图来说，表示的图中节点的拓扑关系。Pattern在图中的实例化叫做match，相当于在图中找到了这种拓扑关系表示的真实案例，这里涉及到的概念是图之间的同态，节点和边都要相互对应，此外还要label的对应。可以看出，label主要是被 pattern match 所用到，可以带有语义地确定图中的某个拓扑结构。
Pattern和规则是紧耦合的，规则对于图来说是不是合适，和Pattern在图中能够找到match很有关系。试想，如果提出一条规则，但是这个规则中蕴含的节点之间的拓扑关系并不能在图Q中体现，那这条规则要如何作用呢？ 因此，一般来说，规则都是在真实的图中挖掘出来的。下面使用h(x)来表示pattern在图G上的匹配。
规则的作用方式是通过已知数据之间的关系来进行某些活动。 上面提到了图规则中的拓扑结构如何确定，规则中的“数据约束”通过最开始介绍‘谓词’进行逻辑推导实现。
图中每个节点都有自己的属性，这可以看作是节点的数据，针对这些数据，可以创建出“节点的特征”。 x,y代表节点，A，B代表属性：x.A=c和x.A=y.B是两种谓词，一种是使用常数绑定，另一种是通过变量的绑定。
有了上述的说明和定义，图规则的定义就很清晰了Q[x](X -> Y)。

图规则的应用

在大数据的场景下，能做的事情有很多：数据一致性检测、知识发现、欺诈检测... 在不同的领域中，根据目标的不同，可以应用带有不同特征的规则。
Eg. 银行欺诈账户检测 在银行开户时，银行会保留用户的家庭地址以及电话号码。如图1所示，一个欺诈团伙，如果能够找到三个有效地址和电话号码，那么就能够开9个银行账户，这样的pattern具有一定的特点，那么就可以根据这种模式进行欺诈账户筛选。
Eg. 数据一致性检验 数据库中可能有一些错误的信息，这些信息能够通过规则检测出来。 在图2的pattern中，可以应用这样的规则 Q2[x,y](y.type="video game" -> x.type="programmer")。当然，这里假定只有程序员才能够作出电子游戏。

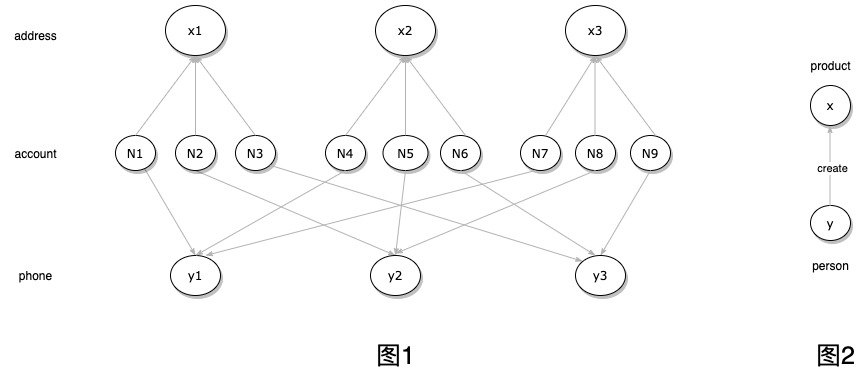
上面提到的场景对于涉及大数据的各个领域来说是很常见的。可以想见，规则的发现和应用是跟应用紧密联系的，一家公司，如果想要根据用户的数据来开发某种应用，这时候根据目的创造出来的规则一定是有意义的。

图规则的语义及种类

规则 \(\varphi\) 作用在图G上的语义是怎么样呢？这里给出一些定义： 对于 \(\varphi\) 在图G上的匹配h(x)以及规则中的lateral，如果lateral中的关系能够在h(x)对应的点中得到满足，那么就说h(x)满足该lateral；如果 h(x) 满足 Y 当且仅当 h(x)满足X，那么h(x)满足 \(\varphi\) 。当然，因为图数据的schemaless的特性，lateral中某个点涉及的属性并不一定能够在h(x)中体现，这时，如果该lateral存在于X中，h(x)满足X，如果上述lateral存在于Y中，那么该lateral就一定要在h(x)中体现。
如果\(\varphi\) 在G中的所有匹配都能够满足 \(\varphi\)，就说 G是满足 \(\varphi\) 的，如果G不满足\(\varphi\) ，说明规则检测出了G中的不一致和问题。
通过前面的例子可以看出，图规则的使用和面对的场景是有很大关系的。如果检测的只是图中节点数据之间的相等关系，那么上述两种谓词（lateral）就足够了；但是如果要添加实体匹配功能（判断两个节点指向的是不是同一个物体），就需要添加新的谓词，将节点的id拿出来显式使用。 而如果想要判断几个节点值之间的关系或者是不等关系可能就需要添加四则运算符号和不等号的语义了，比如，一个国家的总人口等于男性人口 + 女性人口。 这里涉及到的是三个节点，使用到了加法的语义。
总之，方法总是随着问题的出现而诞生的。

规则涉及的几个问题

满足问题Satisfiability

给定一些同类的规则集 \(\Sigma\) 判断对于这些规则，是否存在一个图G，使得图G满足每条规则，如果存在这样的图，称其为 \(\Sigma\) 的模型。 如果对于规则集 \(\Sigma\) 存在模型，说明规则集里面的规则都是合理且不冲突的。

推导问题Implication

给定一个同类的规则集 \(\Sigma\) 和另一条规则 \(\varphi\)，如果对于任意有限图G， 如果图G满足 \(\Sigma\)，就有G满足\(\varphi\)，称\(\Sigma\)能够推出 \(\varphi\)。 推导分析能够找出规则集合中的重复规则。

验证问题Validation

给定图G以及规则集合 \(\Sigma\)，判断图G是否能够满足\(\Sigma\)。