Codeforces Round 419 (Div. 2) 解题报告
对应场次为 CF816 九条可怜场
A. Karen and Morning

题目大意
给你一个时刻(形如hh:mm)你需要输出至少再经过多少分钟 这个时刻会变成一个回文串‘
Solution
看着很唬人 结果发现撑死 \(24 \times 60\) 次就转回来了 所以直接暴力枚举答案计算即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 1) + (xr << 3) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
string s;
int h, m;
bool check(int x, int y) {
int tmp = 0;
tmp += y / 10;
tmp += y % 10 * 10;
return tmp == x;
}
void main() {
cin >> s;
h = (s[1] - '0') + (s[0] - '0') * 10;
m = (s[4] - '0') + (s[3] - '0') * 10;
int ans = 0;
while (1) {
if (check(h, m)) {
write(ans);
return;
}
++ans;
++m;
if (m == 60) m = 0, ++h;
if (h == 24) h = 0;
}
}
}
int main() {
steven24::main();
return 0;
}
B. Karen and Coffee
aficionado ...迷
optimal 最佳的
brew 酿造,冲泡
acclaim 宣称,称誉
admissible 可接受的
fickle 反复无常的

题目大意
给你 \(n(1 \le n \le 2 \times 10^5)\) 个区间 给定一个整数 \(k(1 \le k \le n)\) 有 \(q(1 \le q \le 2 \times 10^5)\) 询问 每次询问区间 \(\left[l, r\right]\) 中有多少个点被至少 \(k\) 个区间覆盖
保证 \(1 \le l \le r \le 2 \times 10^5\)
Solution
解法一:魔怔的 DS 人
最开始没看到每次询问的 \(k\) 相同 所以用线段树维护区间加操作 然后建出主席树回答询问
解法二:魔怔的 DS 人 2.0
区间加 查询区间有多少个数大于 \(k\)
分块 同P2801 教主的魔法
解法三:前缀和+差分
区间加可以用差分实现
每次询问的 \(k\) 相同 所以直接使用前缀和数组记录 \(\left[1, i\right]\) 的答案个数即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 1) + (xr << 3) + (cr ^ 48), cr = getchar();
return xr * F;
}
void write(ll x) {
char ws[51];
int wt = 0;
do {
ws[++wt] = x % 10 + '0';
x /= 10;
} while (x);
for (int i = wt; i; --i) putchar(ws[i]);
}
namespace steven24 {
const int N = 2e5 + 0721;
int d[N], f[N];
int n, k, q;
void main() {
n = read(), k = read(), q = read();
for (int i = 1; i <= n; ++i) {
int l = read(), r = read();
++d[l], --d[r + 1];
}
for (int i = 1; i <= 200000; ++i) d[i] += d[i - 1];
for (int i = 1; i <= 200000; ++i) if (d[i] >= k) ++f[i];
for (int i = 1; i <= 200000; ++i) f[i] += f[i - 1];
while (q--) {
int l = read(), r = read();
write(f[r] - f[l - 1]), putchar('\n');
}
}
}
int main() {
steven24::main();
return 0;
}
C. Karen and Game
fixate 异常依恋

题目大意
给定一个 \(n \times m (1 \le n, m \le 100)\) 的矩阵 初始有一个全0矩阵 每次操作可以把一行或者一列所有数+1 问最少操作次数并输出方案 若无解输出-1
\(0 \le a_{i, j} \le 500\)
Solution
考虑倒过来做 即把给出的矩阵删成全0矩阵
那么如果按行考虑 设这行最小的数为 \(x\) 直接对这一行操作 \(x\) 次即可
然后再按列同理做一遍 如果都做完了还有剩的就无解
但是发现 如果行数 > 列数时 有可能先删列反而更优 比如下面这个:
5 3
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
所以行列哪个小先从哪个开始删即可
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
namespace steven24 {
const int N = 105;
int a[N][N];
int max_row[N], max_col[N];
int n, m;
void solve1() { //处理行的
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) max_row[i] = min(max_row[i], a[i][j]);
for (int j = 1; j <= m; ++j) a[i][j] -= max_row[i];
}
}
void solve2() { //处理列的
for (int j = 1; j <= m; ++j) {
for (int i = 1; i <= n; ++i) max_col[j] = min(max_col[j], a[i][j]);
for (int i = 1; i <= n; ++i) a[i][j] -= max_col[j];
}
}
void main() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) a[i][j] = read();
memset(max_row, 0x3f, sizeof max_row);
memset(max_col, 0x3f, sizeof max_col);
if (n < m) solve1(), solve2();
else solve2(), solve1();
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (a[i][j]) {
puts("-1");
return;
}
}
}
int ans = 0;
for (int i = 1; i <= n; ++i) ans += max_row[i];
for (int j = 1; j <= m; ++j) ans += max_col[j];
printf("%d\n", ans);
for (int i = 1; i <= n; ++i) for (int k = 1; k <= max_row[i]; ++k) printf("row %d\n", i);
for (int j = 1; j <= m; ++j) for (int k = 1; k <= max_col[j]; ++k) printf("col %d\n", j);
}
}
int main() {
steven24::main();
return 0;
}
//g++ test.cpp -o test -O2 -Wall -fsanitize=address,leak,undefined
D. Karen and Test

题目大意
给定一个长度为 \(n(1 \le n \le 2 \times 10^5)\) 的序列你需要对这个序列之中的每两个数之间从加开始加减交替进行操作
问最后剩下那个数是多少 放一下样例解释理解一下
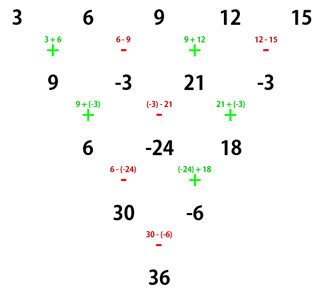
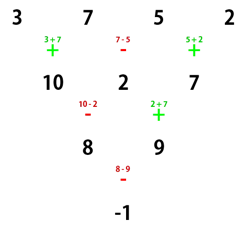
Solution
不难想到计算每个数的贡献 问题是怎么算
通过自己手动构造加减的三角阵 发先 \(n\) 每次+2 开头的符号就要改变
或者说 4/5/8/9 的加减三角阵是包含关系
所以本质上我们只需要求两种加减三角阵中元素的贡献
感觉比较好的方法就是手动打表了
然后就能发现以下式子

对于1/3的状况 我们把第一行暴力做掉就可以转化成以上两种情况了
写的时候特判没 return 蠢到家了
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
int xr = 0, F = 1;
char cr;
while (cr = getchar(), cr < '0' || cr > '9') if (cr == '-') F = -1;
while (cr >= '0' && cr <= '9')
xr = (xr << 3) + (xr << 1) + (cr ^ 48), cr = getchar();
return xr * F;
}
namespace steven24 {
const int N = 2e5 + 0721;
const int mod = 1e9 + 7;
ll fac[N], inv[N];
int a[N];
int n;
void init() {
fac[1] = inv[1] = 1;
fac[0] = inv[0] = 1;
for (int i = 2; i <= n; ++i) {
fac[i] = fac[i - 1] * i % mod;
inv[i] = (mod - mod / i * inv[mod % i] % mod) % mod;
}
for (int i = 2; i <= n; ++i) inv[i] = inv[i] * inv[i - 1] % mod;
}
ll C(int m, int n) {
if (m > n) return 0;
else return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
void main() {
n = read();
init();
for (int i = 1; i <= n; ++i) a[i] = read();
if (n == 1) {
printf("%d\n", (a[1] + mod) % mod);
return;
}
if (n & 1) {
for (int i = 1; i < n; ++i) {
if (i & 1) a[i] = (a[i] + a[i + 1]) % mod;
else a[i] = (a[i] - a[i + 1]) % mod;
}
--n;
}
ll ans = 0;
int op = 1;
for (int i = 1; i <= n; ++i) {
int m = (i - 1 >> 1);
ans = (ans + a[i] * op * C(m, (n - 2 >> 1)) % mod) % mod;
if (n % 4 == 0) op *= -1;
}
printf("%lld\n", (ans + mod) % mod);
}
}
int main() {
steven24::main();
return 0;
}
//g++ test.cpp -o test -O2 -Wall -fsanitize=address,leak,undefined
E. Karen and Supermarket

题目大意
超市里有 \(n(1 \le n \le 5000)\) 种商品 每个商品的价格为 \(c_i\)
另有 \(n\) 张优惠券 第 \(i\) 张可以让第 \(i\) 个商品的售价减少 \(d_i\) 但除了第一张以外 剩余的优惠券使用时必须同时使用第 \(x_i\) 张优惠券
可怜有 \(B\) 的预算 请问她最多可以买多少商品
Solution
发现每张券只绑定了一张其他的券 考虑建树
发现将预算放进状态里不好转移 但是把商品数放进状态里很好转移
设 \(f_{i, j, 0/1}\) 表示考虑 \(i\) 子树中的所有商品 选了 \(j\) 个 未使用/使用优惠券的最小花费
有:
- \(f_{x, j + k, 0} = \min(f_{x, j, 0} + f_{y, k, 0})\)
- \(f_{x, j + k, 1} = \min(f_{x, j, 1} + f_{y, k, 0})\)
- \(f_{x, j + k, 1} = \min(f_{x, j, 1} + f_{y, k, 0})\)
初始化: - \(f_{x, 0, 0} = 0\)
- \(f_{x, 1, 0} = c_i\)
- \(f_{x, 1, 1} = c_i - d_i\)
使用树上背包转移 复杂度为 \(\text{O}(n^2)\)
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5210;
ll f[N][N][2];
int siz[N];
int c[N], d[N];
int head[N], to[N << 1], nxt[N << 1], cnt;
int n, b;
inline void add_edge(int x, int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x, int fa) {
siz[x] = 1;
f[x][1][0] = c[x];
f[x][1][1] = c[x] - d[x];
f[x][0][0] = 0;
for (int i = head[x]; i; i = nxt[i]) {
int y = to[i];
if (y == fa) continue;
dfs(y, x);
for (int j = siz[x]; j >= 0; --j) { //注意写法 不然复杂度会退化
for (int k = 0; k <= siz[y]; ++k) {
f[x][j + k][1] = min(f[x][j + k][1], f[x][j][1] + f[y][k][1]);
f[x][j + k][1] = min(f[x][j + k][1], f[x][j][1] + f[y][k][0]);
f[x][j + k][0] = min(f[x][j + k][0], f[x][j][0] + f[y][k][0]);
}
}
siz[x] += siz[y];
}
}
int main() {
memset(f, 0x3f, sizeof f);
scanf("%d%d", &n, &b);
for (int i = 1; i <= n; ++i) {
int x;
scanf("%d%d", &c[i], &d[i]);
if (i != 1) {
scanf("%d", &x);
add_edge(x, i);
add_edge(i, x); //写到这才发现是有根树 但是懒得改dfs了所以就建了双向边
}
}
dfs(1, 0);
for (int i = n; i >= 1; --i) {
if (f[1][i][1] <= b || f[1][i][0] <= b) {
printf("%d", i);
return 0;
}
}
printf("0");
return 0;
}
F. Karen and Cards
看不明白题解 只能自己悟一悟

题目大意

Solution
首先按 \(a_i\) 排序使一维有序
然后考虑枚举 \(a\)
当 \(a \in \left(a_i, a_{i + 1}\right]\) 时 分两部分考虑
对于 \(\left[i + 1, n\right]\) 这段的 给的限制就是 \(b > \max b_i\) 且 \(c > \max c_i\)
对于 \(\left[1, i\right]\) 这段 考虑每个元素给的限制:
- 当 \(b > b_i\) 时 \(c\) 无要求
- 当 \(b \le b_i\) 时 \(c > c_i\)
首先对于后者 我们可以开一棵线段树 \(i\) 表示 \(b = i\) 时能取到 \(c_i\) 的最小值
这样每个限制条件形如对一段前缀区间赋值然后取 \(\max\)
看起来需要吉司机 但是不难发现形态一定是一个不断向下的阶梯状 所以直接在线段树上二分找到左端点即可
然后考虑前者条件 显然我们要查询 \(\max b_i + 1\) 之后的区间
对于 \(c\) 的限制 我们先临时给全局像上面一样赋一个 \(\max c_i\)
然后发现实际合法答案数就是总答案数-区间和(即不合法的答案数)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号