线段树合并

默认你会线段树了，要不然会来看这个？

众所周知，如果两棵线段树的形状相同、维护的信息相同，那么这两棵线段树就可以相加得到一棵新的线段树。所以说线段树具有可加性。

举个例子，如果要合并下面两棵树：

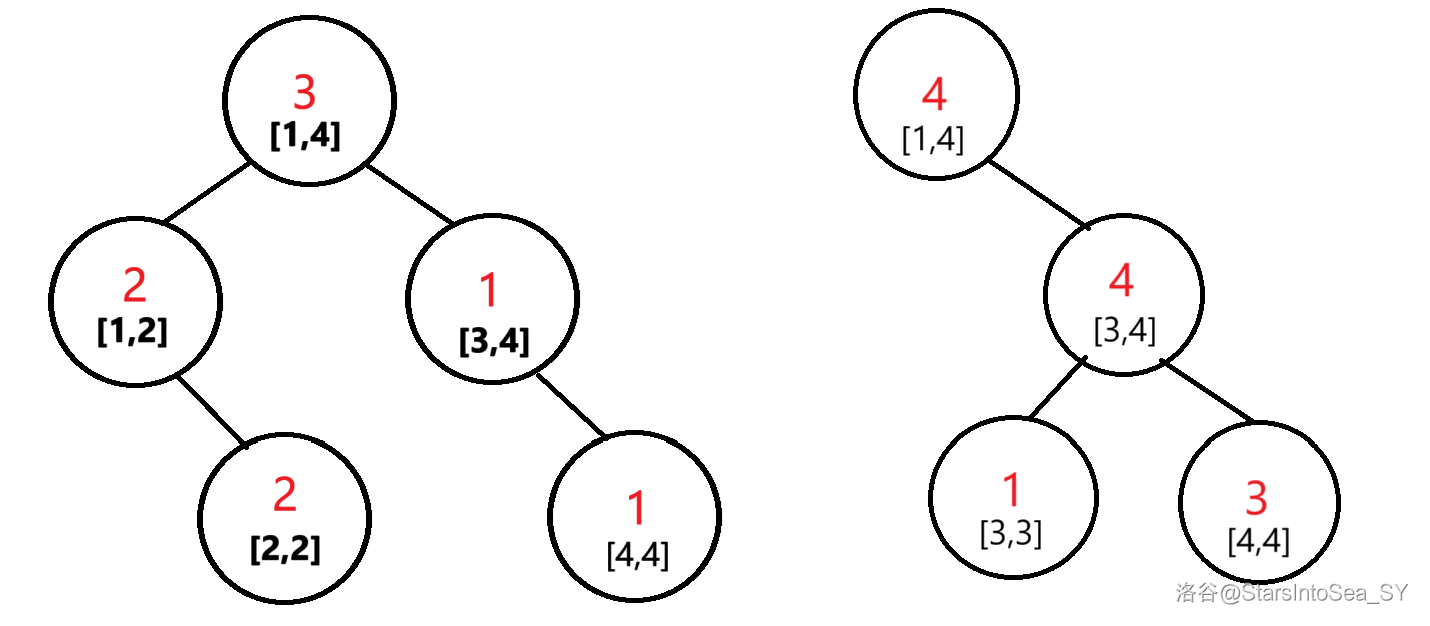
合并后是这样的：

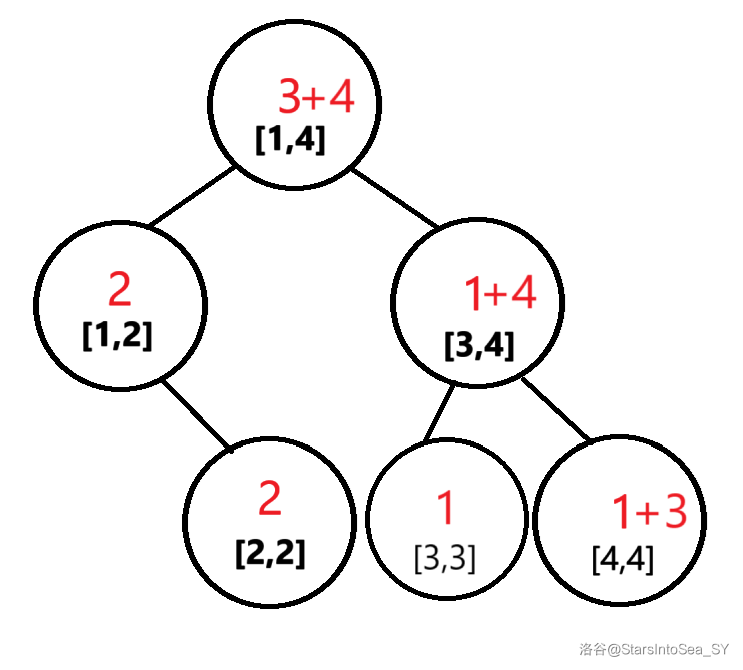
核心代码：

//把编号为 y 的线段树合并到编号为 x 的线段树中
int merge(int x,int y,int l,int r){
	if(!x||!y) return x|y; //如果这两个节点其中一个为空就返回另一个
	// do something
	if(l==r){
		//do something
		return x;
	}
	lc[x]=merge(lc[x],lc[y],l,mid);  //合并左子树
	rc[x]=merge(rc[x],rc[y],mid+1,r); //合并右子树
	//do something
	return x;  //返回当前节点
}
rt[x]=merge(rt[x],rt[y],1,n);

不难看出合并的时间复杂度是两棵线段树的并集大小。

在合并的过程中，有些点是通过运算后得到的（如果这个点在原树和被合并的树中存在），有些是通过直接连接边得到的（如果这个点在合并的原树中不存在）。因为后者连边的特性，被合并的树在合并后会受到原树的影响，因此，一旦一个树被合并就要直接抛弃，不要再次使用。

线段树合并常用在树上或图上的一些信息维护。

一般的线段树合并题都是权值线段树合并。

线段树合并通常需要前缀和和差分的思想。

线段树分裂很简单，就是合并的逆操作，仿照 FHQ-Treap 或者自己手动模拟就能写出来。

这东西光说是没用的，得看例题：

CF600E Lomsat gelral

板子题。

树上每个节点开一棵权值线段树统计自己子树内的颜色情况，先把自己加上去然后 dfs，把自己的儿子的线段树合并到自己身上统计答案。

P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

对树上的每个点都开一个权值线段树来记录这个点的救济粮情况。

一个点一个点加是不可能的，考虑树上差分。

比如要在 \(u\) 到 \(v\) 的路径上加救济粮，就是 \(u\) 节点的权值线段树对应位置 +1，\(v\) 节点 +1，\(LCA\) 和 \(LCA\) 的爹是 -1，然后 dfs 向上合并，把儿子的信息合并到爹身上，统计答案即可。

P3224 [HNOI2012] 永无乡

开一个并查集维护联通块。

每次访问一个点的联通情况时，直接用并查集找它的祖宗，这样只需要在祖宗的线段树中找答案就行。

需要合并时就把两棵线段树合并到新的祖宗上，合并时要启发式合并，不然复杂度会假。