题解：CF2117F Wildflower

CF2117F Wildflower

更洛谷的阅读体验

好题，爽！

思维题，爽！

Ad-hoc，爽！

我做出来了，爽飞了！

思路

首先我们发现由于每个点的权值只可能是两种情况，所以一旦出现三个及以上的叶子节点就肯定出现了相同的子树权值和，此时的答案为 0。

那么合法的树就只有两种形态，一种直接退化成链，另外一种只有一个节点有两个子节点，如下图。（有点丑见谅）

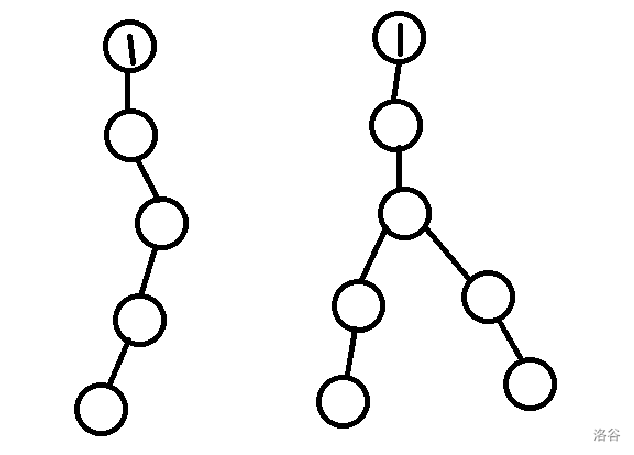
先看一条链的情况，容易发现此时怎么填都合法，假设有 \(n\) 个节点，每个节点有两种情况，答案显而易见的就是 \(2^n\)。

看第二种情况，我们发现出现分叉之前的节点和链的情况是一样的，只需要考虑两个分支怎么填。

我们假设剩下的这两条链长度相同，从最下面的两个叶子考虑，肯定是一个为 1 一个为 2，往上走只要有一个填了 1 就肯定会出现重复，这是显然的，可以自己手模一下。
也就是说，最终这两条链的子树权值和从下往上的数列一定是一个全是奇数一个全是偶数，就只有两种可能，和它上面的链的答案再拼起来，我们设分叉前的链长为 \(l\)，答案就是 \(2^{l + 1}\)。

考虑最后一种情况，即两个分支的长度不相等，如下图：

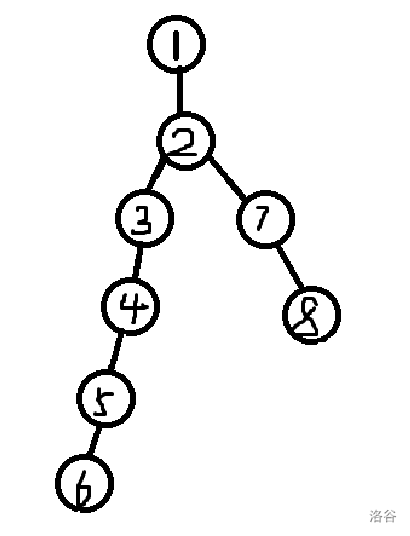
我们先从下往上同时填数直到较短链到达两个叶子的 LCA，目前已经填好权值的节点是 \(5\)、\(6\)、\(7\)、\(8\)，此时还是两种可能。

目前看来好像是没有问题的，和上一种情况一样，然后我们考虑节点 \(4\)。

设节点 \(x\) 的权值是 \(a_x\)，注意到当 \(a_5 = 2\)，\(a_6 = 1\)，\(a_7 = 2\)，\(a_8 = 2\) 时，\(a_4 \neq 1\)。因为此时 \(s_4 = s_7 = 4\)，不符合题意，所以从节点 \(4\) 到节点 \(8\) 的合法的情况只有 3 种。

形式化地，设较短链长为 \(len\)，这棵树的最大深度为 \(dep\_max\)，答案应为 \(2^{dep\_max - len - 1} \times 3\)。

我们按照上面的方法分类讨论即可。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int MN = 2e5 + 3, mod = 1e9 + 7;
int n, dep[MN], ans, len;
vector<int> rec;

int head[MN], tot;
int to[MN << 1], nx[MN << 1];
void add(int x, int y) {
    to[++tot] = y;
    nx[tot] = head[x];
    head[x] = tot;
}

void dfs(int x, int fa) {
    dep[x] = dep[fa] + 1;
    int fl = 0;

    for (int i = head[x]; i; i = nx[i]) {
        int y = to[i];
        if (y == fa) continue;
        fl++;
        dfs(y, x);
    }
    if (fl == 0) rec.push_back(dep[x]);
    else if (fl > 1) len = dep[x];
}

int power(int a, int b) {
    int res = 1;
    for ( ; b; b >>= 1, a = a * a % mod)
        if (b & 1) res = a * res % mod;
    return res;
}

void fir();
void solve() {
    cin >> n;
    fir();
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y);
        add(y, x);
    }

    dfs(1, 0);
    if (rec.size() > 2) return cout << "0\n", void();
    if (rec.size() == 1) {
        int x = rec[0];
        return cout << power(2, x) << "\n", void();
    }

    int mn = mod, mx = 0;
    for (int x : rec) {
        mn = min(mn, x);
        mx = max(mx, x);
    }

    if (mn == mx) return cout << power(2, len + 1) << "\n", void();
    else {
        int tmp = mn - len;
        int tl = mx - tmp - 1;
        ans = power(2, tl) * 3 % mod;
        cout << ans << "\n";
    }
}

inline void fir() {
    ans = tot = 0;
    len = 0;
    for (int i = 1; i <= n; i++) head[i] = 0;
    rec.clear();
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);

    int T;
    cin >> T;
    while (T--) solve();
    return 0;
}