题解：二分图最大匹配

P3386【模板】二分图最大匹配

喵

写在前面

这是一篇匈牙利算法求二分图最大匹配的题解。

我会尽量写的详细一些好让大家都能看懂。。。
所以会比较啰嗦，还请各位耐心看完。

图都是用鼠标画的，比较丑，还请多多包涵。(OvO----)=3

部分内容参考 oiwiki，之前学长上课用的课件与这篇文章。

What is 二分图？

二分图，又叫二部图。
二分图由两个集合构成，且集合内部没有边相连。

如下图，有两个集合 \(u\) 与 \(v\)，属于同一集合的两个点之间没有边相连，但是不在同一集合内的点是可以连边的。

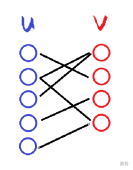
换言之，存在一种方案，可以把点分为两个集合且满足以上条件。

二分图的性质

• 若我们将二分图的两个集合中的点分别染成黑色和白色，那么每一条边都连着一个黑色的点和一个白色的点。
• 二分图里不存在奇环。

第一条很好理解，我们还是观察上图，发现每一条边都连着两个颜色不同的点。
当然我们从定义的角度出发，在同一集合内的点是不能连边的，故也不存在同时连接了两个颜色相同的点的边。

第二条，我们发现若想从一个集合出发再回到该集合，需要从这个集合出去再回来，这样的话就只能是偶数条边，故不可能存在奇环。

二分图的匹配

在二分图中选出一些边作为一个集合，使任意两条边不存在公共点，那么我们称其为一个匹配。

还是看图，这个就是一个匹配：

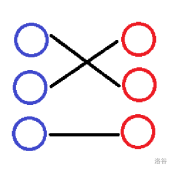
而在这张图里，我们发现有一些边是由公共点的，那它就不是一个匹配：

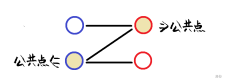
同时二分图的边满足所连接的两个端点都属于不同的两个集合中。

本题让我们求解二分图的最大匹配，即让这个匹配的边数最多，那么此时这个图就是该二分图最大匹配。

二分图最大匹配的求解

求最大匹配之前，我们先了解一些概念。

交替路

从一个未匹配的点出发，依次经过未匹配边、匹配边、未匹配边、匹配边。。。这样的路线叫交替路。

增广路

从一个未匹配的点出发，走交替路，到达了一个未匹配的点，那么这条路就是增广路。

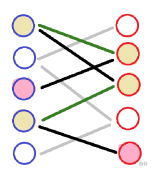
（黄色的是匹配点，粉色的是非匹配点同时是路的起点终点，绿色的是匹配边，黑色的是增广路上的非匹配边，灰色的边是其他边）
不考虑灰色的边，剩余的边构成增广路，可以看着图走一走。

增广路性质总结：

• 增广路一定由奇数条边构成。
• 增广路的起点和终点都是未匹配点。
• 路径上的相邻的点不在同一集合内。
• 在增广路上，非匹配边一定比匹配边多一。

PS：最大匹配是不存在增广路的，否则可以通过翻转得到更大的匹配（后面会专门说这部分的证明）。

那么我们就可以利用这个性质去求解最大匹配。

匈牙利算法

匈牙利算法就是通过找增广路来求最大匹配。

也有人说它的思想本质就是网络流的（不过我不会网络流）。

那么匈牙利算法是怎么实现的呢？

如果想看有意思的解释请点这里，我没那个实力就写写最普通的解释吧。。。

现在有一张二分图：

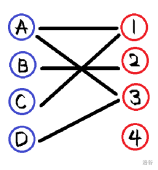
我们要给他们尽量多的配对这样就能求出最大匹配了。

那么我们从 \(A\) 点开始配对，让我看看。。。就 \(1\) 吧！

同样地，我们也可以将 \(B\) 与 \(2\) 配对，那么这张图就变成了这样（涂黄的为匹配点，绿边为匹配边）：

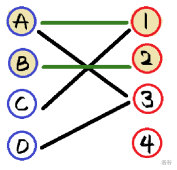
接着我们给 \(C\) 配对，但是我们发现一个问题，它能配对的点 \(1\) 已经有了配对，怎么办呢？

有了！我们看看 \(A\) 能不能换一个不就行了。

于是，\(A\) 去找了 \(3\)，现在 \(C\) 就能愉快的与 \(1\) 配对了！

（这一步就是在寻找增广路，\(C\) 是一个未匹配点，那么若我们能够找到一条以它为起点的增广路：\(C\)-\(1\)-\(A\)-\(3\)，说明存在更大的匹配，这时我们将增广路翻转就有了更大的匹配）。

操作后如下图：

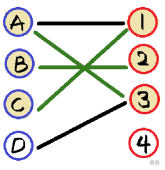
然后是 \(D\)，我们发现它想要的 \(3\) 已经配对了，那么只好和 \(A\) 商量能不能让它换一个。
（同样是配对失败寻找增广路）。

但 \(A\) 想配对的点已经都配好对了，于是 \(D\) 遗憾离场。

（没有以 \(D\) 为起点的增广路，\(D\) 配对失败）。

然后就有这张二分图的最大匹配啦！

（结合前面我们说的，就是找不到增广路了，那么此时就有最大匹配）。

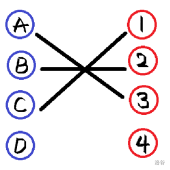
那么答案就是 \(3\)。

正确性证明

Q：为什么用匈牙利算法求解二分图最大匹配是正确的呢？

首先匈牙利算法是通过寻找增广路来寻找更大的匹配。

也就是说，如果我们用匈牙利算法求出了一个二分图的最大匹配，那么这个匹配里是没有增广路的。

此时问题转化为：如何证明二分图的最大匹配中不存在增广路。

我们回看上面最大匹配的图（我这里直接搬下来这样就不用来回翻了）：

（左图绿色为匹配边）
应该是不会在上图找到增广路的，有的话可能是我图画错了。

还是看有增广路的图，我们此时不考虑灰色的边，当它不存在。

（黄色的是匹配点，粉色的是非匹配点，但同时是路的起点终点，绿色的是匹配边，黑色的是增广路上的非匹配边）

显然这个匹配肯定不是最大匹配。

为什么？

用反证法。

我们先假设这个就是最大匹配，那么此时图上肯定不存在更大的匹配。

接下来证明这个假设是错误的。

也许你还记得增广路有这一条性质：

• 在增广路上，非匹配边一定比匹配边多一。

再结合增广路的定义，可以说增广路就是特殊的交替路。

此时我们就翻转一下。

即将匹配边变为非匹配边，非匹配边变为匹配边。

由于原来匹配边比非匹配边少一，那么翻转后就有匹配边比非匹配边多一。

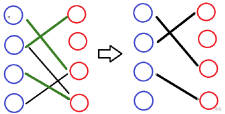
翻转过后如图：

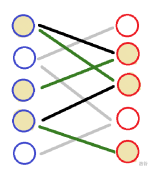
这张图上存在更大的匹配，上面的假设不成立。

即二分图的最大匹配中不存在增广路。

证毕。

实现思路

首先要存图。

这里我用的是 vector。

连好边之后我们可以从每一个左部点出发寻找与他相连的右部点，都跑一遍匈牙利去匹配 or 找增广路。成功的话就 ans++。

怎么样是不是很简单？

然后我们就可以写出下面的代码：

vector edge[MN]; //存图
int rec[MN]; //记录谁和谁匹配了

bool dfs(int x) {
    for (auto y : edge[x]) //遍历当前节点连的所有边（点）
        if (rec[y] == 0 || dfs(x)) { //边的另一端的点未匹配 or 找到了一条增广路
            rec[y] = x; //记录
            return true;
        }

    return false;
}

int main() {
    //略

    int ans = 0;
    for (int i = 1; i <= n; i++) //遍历所有左部点 
        if (dfs(x)) ans++;
}

然后。。。（没记错的话喜提 10pts）。

为什么？

不保证给出的图没有重边。

难道我们就要放弃 vector 了吗？

不。

我们发现如果输入了重边，在遍历的时候都会从同一个点出发。

这句话听起来像是一句废话。。。
但是我们可以利用这个根据每个左部点访问顺序给每一个右部点打上时间戳，如果当前轮次已经访问过了就直接返回 false。这样就避免了重边的影响。

由于我们遍历每一个左部点（有 \(n\) 个）时再枚举与其相连的右部点（最多 \(m\) 个），时间复杂度就是 \(O(nm)\)。

如果还是有疑惑的话，可以结合代码食用～

代码（不要直接跳到这里啊喂）

#include <bits/stdc++.h>
using namespace std;

int n, m, e, ans;
int tim[505]; //时间戳防重边
int rec[505]; //记录谁与谁配对
vector < int > edge[505]; //存边

bool dfs(int x, int t) { //当前节点, 时间戳
    if (tim[x] == t) return false; //当前轮次已访问直接返回

    tim[x] = t; //标记

    for (auto y : edge[x]) 
        //遍历到的右集合内节点未访问 or 可以找到增广路径
        if (rec[y] == 0 || dfs(rec[y], t)) {
            rec[y] = x; //匹配
            return true;
        }

    return false;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);

    cin >> n >> m >> e;
    for (int i = 1; i <= e; i++) {
        int x, y;
        cin >> x >> y;
        edge[x].push_back(y);
    }

    for (int i = 1; i <= n; i++)
        if (dfs(i, i)) ans++;

    cout << ans << endl;

    return 0;
}