状压DP学习笔记

前言：

最近学了这个神奇的东东，真的好难啊_{[仙女叹气]}~

感觉自己没大理解，就写笔记强迫自己学会吧QAQ

定义：

状态压缩动态规划，就是我们俗称的状压\(DP\)，是利用计算机二进制的性质来描述状态的一种\(DP\)方式。

自己的小理解：其实就是将状态压缩成二进制下的数（\(1/0\)）来表示两种不同情况从而进行暴力枚举\(DP\)……所以只适用于小范围的数据且对于 \(dp\) 状态有要求（只能有两种不同情况）

复习总结：

如何确定考察知识点为 状压 dp

最明显的就是数据范围，如果数据范围 \(n <= 20\) 而且题面隐隐有 \(dp\) 的味道，那大概就是状压没跑了。

定义状态

将状态压成二进制数，这不用说了。

要特别考虑的是 无后效性。

后效性是指如果在某个阶段上过程的状态已知，则从此阶段以后过程的发展变化仅与此阶段的状态有关，而与过程在此阶段以前的阶段所经历过的状态无关。利用动态规划方法求解多阶段决策过程问题，过程的状态必须具备无后效性。——摘自百度百科。

也就是说，如果我们定义 \(dp[i][sta]\) 为第 \(i\) 行状态为 \(sta\) 时的方案数，那么为了保证无后效性,

\(dp[i][sta]\) 只受第 \(i - 1\) 行的影响，同时只能影响第 \(i + 1\) 行。只有这样，才能保证 \(dp\) 的可行性。

如果 \(dp\) 状态不止两种怎么办

大多数情况只能放弃。。。说明你应该换个思路了。

但是有些题目有迷惑性，翻译成人话就是：题面的多种情况就是在扯淡。

例如「BZOJ3864 HDU4899」Hero meet devil

前置知识：

位运算；
\(DP\)；
以及一个聪明的小脑袋瓜；

位运算介绍：

一个神奇的东西……

推荐博客

状压\(DP\)里主要用到的几个技巧见下图：

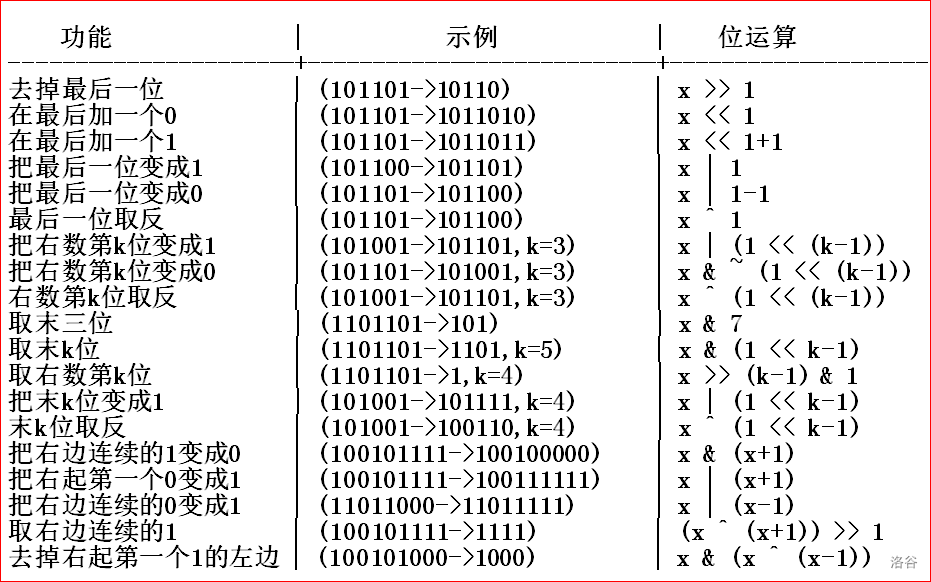
状压DP常用的二进制技巧

引入：

互不侵犯

题目

在 \(N×N\) 的棋盘里面放 \(K\) 个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到他周围的 \(8\) 个格子。

\(dp[i][j][k]\) 表示第 \(i\) 行状态为 \(j\) ,一共放了 \(k\) 个国王时的方案数。

当前方案数仅与上一行有关（每一行只需要判断与上一行是否攻击）

状态转移方程：

\(dp[i][j][k] += dp[i - 1][s][k - cnt(s)]\)

\(s\) 为上一行满足条件的状态，\(cnt\) 是上一行摆放的国王数量。

最终答案：

再次枚举每一个状态：

\(ans += dp[n - 1][s][k]\);

#include <cstdio>
#include <cmath>
#include <algorithm>
#define ll long long//不开long long见祖宗 
using namespace std;
int n,k,cnt[1 << 15];
ll ans,dp[15][1 << 15][100];//状态：1表示该位置放了国王，0没有放 
bool flag[1 << 15];
int Count(int x) {
	int res = 0;
	while(x) {
		res += x & 1;
		x >>= 1;
	}
	return res;
}
bool check1(int x) {
	for(int i = 0; i + 1 < n; i ++) {
		if((x & (1 << i)) && (x & (1 << (i + 1))))
			return 0;//如果有相邻的国王，不符条件 
	} 
	return 1;
}
bool check2(int x,int y) {
	for(int i = 0; i < n; i ++) {
		if(x & (1 << i)) { 
			if(y & (1 << i)) return 0;//上为1 
			if(i + 1 < n && (y & (1 << (i + 1)))) return 0;//左上为1 
			if(i - 1 < n && (y & (1 << (i - 1)))) return 0;//右上为1 
		}
	}
	return 1;
}
signed main() {
	scanf("%d %d",&n,&k);
	int m = 1 << n;
	for(int i = 0; i < m; i ++) {
		flag[i] = check1(i);
		cnt[i] = Count(i);
	}//预处理，避免重复 
	for(int i = 0; i < n; i ++) {
		for(int j = 0; j < m; j ++) {
			if(!flag[j]) continue;
			if(!i) dp[i][j][cnt[j]] = 1;
			else {
				for(int h = Count(j); h <= k; h ++) {//枚举此时的国王总数 
					for(int a = 0; a < m; a ++) {//枚举上一行的状态 
						if(!flag[a] || !check2(j,a)) continue;
						dp[i][j][h] += dp[i - 1][a][h - cnt[j]];
					}
				}
			}
		}
	}
	for(int i = 0; i < m; i ++) ans += dp[n - 1][i][k];//从0开始,共有n-1行
	printf("%lld\n",ans);
	return 0;
}

总结：

状压的入门题，思路挺好想的，只是要注意细节。

正文：

炮兵阵地

题目

给定一个 \(N * M\) 的初始状态，规定了哪些位置可以放炮兵。要求每个炮兵前后左右两格不能有他人。求最多可以放多少兵。

数据范围：\(1 \leq N \leq 100\), \(1≤M≤10\).

因为每一行的情况与前两行有关，就要定义三个状态，又因为当前状态可以有前一行转移而来，所以只用定义当前状态和前一行的状态，前前行的状态可以由前一行表示，所以定义：

\(dp[i][j][k]\)，表示第 \(i-1\) 行状态为 \(j\) ,第 \(i\) 状态为 \(k\)。

然后再循环枚举 \(dp[i - 1][h][j]\) (表示第 \(i-2\) 行状态为 \(h\)).

这样就可以确定三行的状态~

又因为很多状态是不符合题意的，直接用 \(dp\) 存储状态太浪费空间。所以可以提前预处理出满足条件的状态，用 \(map[]\) 存下来，重新定义 \(dp[i][j][k]\) 为第 \(i-1\) 行状态为 \(map[j]\) ,第 \(i\) 状态为\(map[k]\) 时的最大值。这样就轻松多啦~

其它讲解都在代码里啦~

#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,num,ans,cnt,sum[1050],map[1050],f[105],dp[2][1050][1050];
char s[15];
int c(int x) {//计算x状态中 1的个数 
	int res = 0;
	while(x) {
		if(x & 1) res++;
		x >>= 1;
	}
	return res;
}
int main() {
	scanf("%d %d",&n,&m);
	for(int i = 1; i <= n; i ++) {
		scanf("%s",s + 1);
		for(int j = 1; j <= m; j ++) f[i] = (f[i] << 1) + (s[j] == 'P');//预处理初始状态 
	}
	num = 1 << m;
	for(int i = 0; i < num; i ++) { //预处理满足条件的状态 
		if((i & (i << 1)) || (i & (i << 2)) || ( i & (i >> 1)) || (i & (i >> 2))) continue;//如果左右有相邻的情况，跳过 
		map[++cnt] = i;
		sum[cnt] = c(i);
		//记录满足条件的状态及其 1的个数 
		if((i & f[1]) == i) dp[1][0][cnt] = sum[cnt];//初始化第1行
		//如果当前状态与第一行的状态相符，直接赋值 (上一行没有所以状态为0)
	}
	for(int i = 1; i <= cnt; i ++) {//初始化第2行 
		for(int j = 1; j <= cnt; j ++) {
			if(!(map[i] & map[j]) && (f[2] & map[j]) == map[j]) dp[0][i][j] += dp[1][0][i] + sum[j];
			//如果 i状态和 j状态满足条件（同一位置不存在都有炮兵的情况） 当前行的值就可以加上 上一行的i状态的值 再加上 当前行j状态 1的数量 
		}
	}
	for(int i = 3; i <= n; i ++) {//从第三行开始 
		for(int j = 1; j <= cnt; j ++) {//枚举当前状态 
			if((f[i] & map[j]) != map[j]) continue;//如果当前情况不满足初始条件，跳过 
			for(int k = 1; k <= cnt; k ++) {//枚举上一行状态 
				if(map[j] & map[k]) continue;//如果两行不满足条件（同一位置都有炮兵），跳过 
				for(int h = 1; h <= cnt; h ++) {//枚举上上行的状态 
					if(!(map[k] & map[h]) && !(map[j] & map[h])) //判断是否满足情况 
						dp[i & 1][k][j] = max(dp[i & 1][k][j],dp[(i - 1) & 1][h][k] + sum[j]);//取最大值 
				}
			}
		}
	}
	for(int i = 1; i <= cnt; i ++) {
		for(int j = 1; j <= cnt; j ++) {
			ans = max(ans,dp[n & 1][i][j]);//枚举所有情况，取最大值 
		}
	}
	printf("%d",ans);
	return 0;
}

知识点小结：

另外，这里用到了一个状压小技巧。很多时候题目会给定初始状态，就限制了之后的状态枚举。这里就再次用到了二进制小技巧。

这里就以这道题为例：

for(int j = 1; j <= m; j ++) 
	f[i] = (f[i] << 1) + (s[j] == 'P');

如果当前点可以放炮兵，我们就在\(f[i]\)的值左移一位的基础上，再加1，最后\(f[i]\)的值就是当前行的最大值，枚举时的状态不能超过\(f[i]\).

其实这里就是在模拟二进制的形成，计算出满足题意的最大状态值。

Fish

题目

有 \(n\) 条鱼，编号从 \(1\) 到 \(n\)。每对鱼相遇的概率是一样的。如果两条标号为 \(i\) 和 \(j\) 的鱼见面，第一只吃了第二只的概率为 \(p[i][j]\)，则第二只吃掉第一只的概率为 \(1 - p[i][j]\)。求每只鱼最后存活在湖里的可能性。

概率 + 状压 \(dp\)

讲解都在代码里

#include<cstdio>
#include<algorithm>
using namespace std;
int n;
double p[25][25],dp[1 << 20];//dp[i],出现i状态的概率（1:这条鱼活着/0:它被吃啦） 
int c(int x) {//计算1的个数 
	int res = 0;
	while(x) {
		res += (x & 1);
		x >>= 1;
	}
	return res;
}
int main() {
	scanf("%d",&n);
	for(int i = 1; i <= n; i ++)
		for(int j = 1; j <= n; j ++)
			scanf("%lf",&p[i][j]);
	int num = (1 << n) - 1;
	dp[num] = 1;//初始状态，全部鱼都活着的概率为1
	for(int i = num - 1; i; i --) {//倒序枚举状态，鱼越吃越少，1的数量也越来越少……这残忍的现实！ 
		int cnt = c(i);//活着的鱼的数量 
		for(int j = 1; j <= n; j ++) {//枚举这一轮被吃到的鱼的序号 
			if((i & (1 << (j - 1)))) continue;//如果在当前状态下，j为1（鱼没有被吃了），跳过
			for(int k = 1; k <= n; k ++) {//枚举k条鱼吃掉的鱼的编号 
				if(!(i & (1 << (k - 1)))) continue;//如果在当前状态下，k为0（鱼已经被吃了,k吃不到j），跳过
				dp[i] += dp[i | (1 << (j - 1))] * p[k][j] / (1.0 * (cnt + 1) * cnt / 2.0);
				//否则，概率为 当前概率 加上 j位存活时的概率 * k条鱼吃掉j条鱼的概率 * 在所有活着的鱼中恰好选到j,k的概率。 
			}
		}
	}
	for(int i = 0; i < n; i ++) printf("%.6lf ",dp[1 << i]);//只有当前位为1的状态 
	return 0;
}

奖励关

题目

共有 \(K\) 轮，有 \(n\) 种物品，每一轮出现每一种物品的概率 \(\frac{1}{n}\)，物品可选可不选，对于选每一种物品，必须要在前面的轮先选给定的部分物品，每一种物品的价格可正可负。求 \(k\) 轮后按最优方案选择的期望价格。

数据范围：\(1\leq K \leq 100\) ,\(1 \leq n \leq 15\) \(1≤K≤100\),\(1≤n≤15\).

首先看题，概率 \(dp\) 没得跑。

再看数据范围，哦豁！状压 \(dp\)！

这道题不同的是需要倒推，因为正推的话有些情况在转移时选择宝物的概率并不是平均的（有宝物合集的限制），这样就会导致结果出现问题，且最终答案的状态表示十分麻烦（不要问我是怎么知道的！），因此选择倒推。

另外，因为 \(dp\) 的转移至于当前局和前一局有关，所以可以用滚动数组优化一下。

详细讲解都在代码里啦~

#include<cstdio>
#include<algorithm>
using namespace std;
int K,n,x,w[20],num[20];
double p,dp[2][1 << 15];
int main() {
	scanf("%d %d",&K,&n);
	p = 1.0 / n;//选择宝物的平均概率 
	for(int i = 1; i <= n; i ++) {
		scanf("%d",&w[i]);//分值 
		while(~scanf("%d",&x) && x)
			num[i] += 1 << (x - 1);//用二进制数存储 宝物集合 
	}
	int maxn = 1 << n;
	for(int i = K; i >= 1; i --) { //游戏轮数 
		for(int j = 0; j < maxn; j ++) {
			dp[i & 1][j] = 0;//初始化（清空上一次循环的值） 
			for(int k = 1; k <= n; k ++) {//枚举这轮抽到的宝物 
				if((j & num[k]) == num[k])//如果满足k宝物的 宝物集合要求,
					dp[i & 1][j] += max(dp[(i + 1) & 1][j | (1 << (k - 1))] + w[k],dp[(i + 1) & 1][j]);
					//满足最优策略，在拿k宝物和不拿之间选最大值 
				else dp[i & 1][j] += dp[(i + 1) & 1][j];//不满足的话，该状态及为上一次的状态，没有变化 
			}
			dp[i & 1][j] *= p;//最终期望要乘上随机选择一个宝物的概率 
		}
	} 
	printf("%.6lf",dp[1][0]);
	//因为是倒推的，所以最后答案为游戏开始时，未得到任何一个宝物的情况 
	return 0;
}

Survival

题目

有 \(n\) 个 \(Boss\),其中有 \(n-1\) 个小 \(boss\) 必须先全部打完才能打第 \(n\) 个大 \(BOSS\)，打一个小 \(boss\) 要耗体能 \(usei\)，打完后恢复一部分 \(vali\)，一开始体能为 \(100\)，在打的过程中也最多为\(100\)，问能打完全部的 \(BOSS\)? 能，输出 \(clear!!!\)。否则，输出 \(try\) \(again\).

很板的一道题

\(dp\) 的状态定义只有一维

讲解都在代码里……

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n, a[25], val[25], dp[1 << 21];
int main() {
    while (scanf("%d", &n) != EOF) {
        memset(dp, -1, sizeof(dp));
        for (int i = 0; i < n - 1; i++) scanf("%d %d", &a[i], &val[i]);
        scanf("%d", &a[n - 1]);
        dp[0] = 100;//初始生命值为100 
        for (int i = 1; i < (1 << (n - 1)); i ++) {//枚举状态 
            dp[i] = -9999; 
            for (int j = 0; (1 << j) <= i; j ++) {//枚举要打死的小怪 
                if (i & (1 << j) && dp[i - (1 << j)] >= a[j]) { //如果当前状态下小怪被打死而且打死小怪之前的生命值能够打死他 
                    int k = dp[i - (1 << j)] - a[j] + val[j];
                    k = min(100, k);//生命值不超过100 
                    dp[i] = max(dp[i], k);//取最大值 
                }
            }
        }
        if (dp[(1 << (n - 1)) - 1] >= a[n - 1])
            printf("clear!!!\n");//如果打完小怪后的生命值可以打死大怪 
        else printf("try again\n");
    }
    return 0;
}

Rectangular Covering

题目链接

给你一些点。需要用任意个矩阵来覆盖所有的点。每个矩形应至少覆盖两个点，一个点可以被几个矩形覆盖。求所有矩阵面积之和最小是多少。

dp[i] 表示覆盖状态为 i 时的最小矩阵和

先枚举所有任意两点能构成的矩形，能包含的点数状态 lim[i]，以及矩形面积 V[i]

然后枚举每个点的覆盖状态，通过预处理出来的矩形数组处理，求最小值。

其他的看代码处理。


#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = (1 << 15) + 5;
int n, num, x[20], y[20], cnt, lim[N], V[N], dp[N];
int _abs(int x) {
	return x < 0 ? -x : x; 
}
int main() {
	while(~scanf("%d", &n) && n) {
		for(int i = 0; i < n; i ++) scanf("%d %d", &x[i], &y[i]);
		memset(dp, 0x3f, sizeof(dp));
		num = 1 << n, cnt = 0;
		for(int i = 0; i < n; i ++) {
			for(int j = i + 1; j < n; j ++) {
				lim[++cnt] = 0;
				for(int k = 0; k < n; k ++) {
					if((x[k] - x[i]) * (x[j] - x[k]) >= 0 && (y[k] - y[i]) * (y[j] - y[k]) >= 0) lim[cnt] |= (1 << k);
				}
				if(x[i] == x[j]) V[cnt] = _abs(y[i] - y[j]);
				else if(y[i] == y[j]) V[cnt] = _abs(x[i] - x[j]);
				else V[cnt] = _abs(x[i] - x[j]) * _abs(y[i] - y[j]);
			}
		} 
		dp[0] = 0;
		for(int i = 0; i < num; i ++) {
			for(int j = 1; j <= cnt; j ++) {
				if((i | lim[j]) == i) continue;
				dp[i | lim[j]] = min(dp[i | lim[j]], dp[i] + V[j]);
			}
		}
		printf("%d\n", dp[num - 1]);
	}
	return 0;
}

Kefa and Dishes

题目链接

愤怒的小鸟

题目

咕咕咕咕……

总结：

其实状压 \(DP\) 做到最后都是套路~~

一般分为几个步骤：

理解题意，确定\(DP\)状态
思考全面，状态转移方程
顺应思路，明确最终结果

状态定义翻来覆去也就那几个，重点和难点在于转移方程的转移和正确性以及对位运算的灵活运用……

posted @ 2021-01-16 16:13 Spring-Araki 阅读(102) 评论(0) 收藏举报

刷新页面返回顶部

去没人的岛