题解 P4304 【[TJOI2013] 攻击装置】

纪念一下一遍过~

题目链接

题目分析：

大意：在给定位置限制的前提和攻击范围的前提下，求能放置的最多装置数。

将攻击范围更直观的表示出来，如下图：

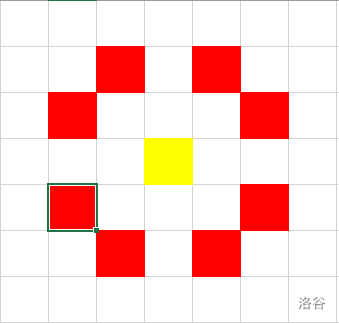
嗯。。。然而并没有神马用。

看题意将攻击坐标表示出来，肯定有用，尝试将横纵坐标的值加起来（为了方便，下文以和代替为横纵坐标之和）：

所以我们发现，攻击坐标的和的奇偶性恰好与原坐标相反，也就意味着和的奇偶性相同的两个点必然不会相互攻击，所以我们就可以利用源汇点将两种点区分开来。

那么建图方式就很显然了：

• 如果和为奇数，从源点向该节点建有向边，边权为\(1\)(题意求的是数量)；
• 反之，从该节点向汇点建有向边，边权为\(1\);

再考虑八个方向的攻击：

因为相互攻击的点不能同时选，所以在两个点之间建有向边，边权为 \(inf\)。

边权为极大值的原因：根据网络流的特性，最小割不能在边权为极大值的边上，所以为了保证割边一定与源点或汇点相连，赋为极大值。

最后，就是模板求最小割了。

完整代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define rt register int
#define int long long
const int N = 4e4 + 10, M = 1e6 + 10, inf = 1e10;
struct node {
	int to,nex;
}e[M];
int n,s,t,top,ed,dep[N],head[N],cur[N],tot = 1,f[M],q[N],ans;
int a[8][2] = {{-1,-2},{-2,-1},{1,-2},{2,-1},{-1,2},{-2,1},{1,2},{2,1}};
char map[205][205];
inline void add(int x,int y,int w) {
	e[++tot] = (node) {y,head[x]}, f[tot] = w, head[x] = tot;
	e[++tot] = (node) {x,head[y]}, head[y] = tot; 
}
inline bool bfs() {
	memset(dep,-1,sizeof(dep));
	dep[s] = 0, cur[s] = head[s], q[top = 1] = s; ed = 1;
	int now,ver;
	while(top <= ed) {
		now = q[top++];
		for(rt i = head[now]; i; i = e[i].nex) {
			ver = e[i].to;
			if(dep[ver] == -1 && f[i]) {
				dep[ver] = dep[now] + 1, cur[ver] = head[ver];
				if(ver == t) return 1;
				q[++ed] = ver;
			}
		}
	}
	return 0;
}
inline int find(int x,int limit) {
	if(x == t) return limit;
	int flow = 0, tmp, ver;
	for(rt i = head[x]; i && flow < limit; i = e[i].nex) {
		ver = e[i].to;
		if(dep[ver] == dep[x] + 1 && f[i]) {
			tmp = find(ver,min(limit - flow,f[i]));
			if(!tmp) dep[ver] = -1;
			f[i] -= tmp, f[i ^ 1] += tmp, flow += tmp; 
		}
	}
	return flow;
}
inline int dinic() {
	int flow;
	while(bfs()) ans -= find(s,inf);
	return ans;
}
inline void read(int &x) {
	x = 0;
	char s = getchar();
	while(s < '0' || s > '9') s = getchar();
	while(s <= '9' && s >= '0') {x = x * 10 + s - '0', s = getchar(); }
}
inline int pos(int x,int y) {
	return n * (x - 1) + y;
} 
signed main() {
	read(n);
	s = n * n + 1, t = s + 1;
	int tx,ty;
	for(rt i = 1; i <= n; i ++) {
		scanf("%s",map[i] + 1);
		for(rt j = 1; j <= n; j ++) {
			if(map[i][j] == '1') continue;
			ans ++;
			if((i + j) & 1) {
				add(s,pos(i,j),1);
				for(rt k = 0; k < 8; k ++) {
					tx = i +a[k][0], ty = j +a[k][1];
					if(tx < 1 || ty < 1 || tx > n || ty > n || map[tx][ty] == '1') continue;//注意要判断该节点是否能放置装置 
					add(pos(i,j),pos(tx,ty),inf);
				}
			}
			else add(pos(i,j),t,1);
		}
	}
	printf("%d",dinic());
	return 0; 
}