04 2018 档案
摘要:多次询问求仙人掌上两点间的最短路径。
阅读全文
摘要:"题目链接" 不同面额的钞票是可以分开考虑的。 ↑其实并不很明白具体(证明?),反正是可以像背包一样去做。 f[x][i][j]表示用前x种面额钞票满足 A有i元 B有j元 (C有sum i j)所需交换的最少数量(=(abs(ΔA)+abs(ΔB)+abs(ΔA+ΔB))/2)。 (i,j是在本来
阅读全文
摘要:"题目链接" 按照优先级移动,操作序列显然是唯一的。 普通的汉诺塔是将n 1个盘子移到中间柱,再将第n个盘子移到目标柱,再将n 1个移到目标柱上的递归过程。 对于本题移动方法还是基本一样的。考虑递推,从i 1个盘子推i个盘子。 p[i][x]表示将x柱上的前i个盘子移走,按顺序操作最终会到哪个柱子上
阅读全文
摘要:"题目链接" POJ输出不能用%lf! mmp从4:30改到6:00,把4:30交的一改输出也过了。 于是就有了两份代码。。 cpp //392K 500MS //用两点构成的矩形更新,就不需要管边界了 include include include include define gc() getc
阅读全文
摘要:"题目链接" "一个比较好的解释?" 模拟退火(Simulated Annealing,SA): (1)初始化一个温度(充分大)、初始解状态S、每个T值的迭代次数。 (2)对i=1,...,L,做(3)至(7)步。 (3)产生新解S'。 (4)计算Δt=C(S') C(S),其中C(S)为评价函数。
阅读全文
摘要:"题目链接" 只有两行,可能的路径数不多,考虑用线段树维护各种路径的连通性。 每个节点记录luru(left_up right_up),lurd,ldru,ldrd,luld,rurd,表示这个区间对应的连通信息。 合并时 横向道路需要用两个数组up[],down[]记录连通性;纵向道路在修改时直接
阅读全文
摘要:"题目链接" 树形DP,考虑子节点对父节点的贡献。 设f[x][i][j]表示当前为x,用i个x去合成上一层装备,花费为j的最大价值。 由子节点转移时 是一个分组背包,需要一个辅助数组g[i][j]表示前i棵子树花费为j能贡献给x的最大价值。 那么 $g[i][j] = max{g[i 1][j k
阅读全文
摘要:"题目链接" "参考" . $Description$ 将$1,2,\cdots,n(n\leq 300)$依次入栈/出栈,并满足$m(m\leq 90000)$个形如$x$要在$y$之前出栈的限制,问合法的出栈序列有多少种。 $Solution$ 没有限制就是个卡特兰数,但有了限制就要考虑好好DP
阅读全文
摘要:"题目链接" $Description$ 将长为$3n$的序列划分成$3$个子序列,要求至少有两个子序列的和都$\geq 500 n$,输出任一方案。保证有解。 $Solution$ 肯定是要将最大的$2n$个数分成两个满足条件的子序列。 直接贪心并没有什么可行的做法。。(反正我想不出来) 我们考虑
阅读全文
摘要:给定无向带权图,求其最小生成树数量,模31011。无重边无自环,且相同权值的边不会超过10条。
$n\leq 100,\ m\leq 1000$。
阅读全文
摘要:给定n*m的格状矩形,每个格子是一个房间或者是一个柱子。一开始时,相邻的格子之间都有墙隔着。
打破墙,使得所有房间形成一棵树。不能打破柱子周围和边界的墙。求方案数,模$10^9$。
$n,m\leq 9$。
阅读全文
摘要:给定长为$n$的字符串,$m$个三种操作:在$p$处插入字符$c$;将$p$处的字符改为$c$;求以两个位置$i,j$开头的字符串的$LCP$。
$m\leq150000$。
阅读全文
摘要:"题目链接" 新写了一篇题解,看这儿吧:https://www.cnblogs.com/SovietPower/p/9775319.html。 显然我们要求出$C(n,m)$为奇数的所有$(n,m)$。 有一个结论: $C(n,m)$是奇数时,有$n\&m==m$。 设$f[i]$为从$A[i]$开
阅读全文
摘要:"题目链接" 设当前为$i$,令$j=\lfloor a i\rfloor$,$1\sim j$ 即为对$i$有贡献的行星,这一区间的答案应为$$f[i]=M_i \sum_{k=1}^j\frac{M_k}{i k}$$ 因为误差不超过$5\%$即可,在这种条件下答案的范围应该非常宽。于是可以将要
阅读全文
摘要:"题目链接" 可以看出我们是要维护一个下凸壳。 先对斜率从小到大排序。斜率最大、最小的直线是一定会保留的,因为这是凸壳最边上的两段。 维护一个单调栈,栈中为当前可见直线(按照斜率排序)。 当加入一条直线l时,可以发现 如果l与栈顶直线l'的交点p在 l'入栈前与栈顶直线 的交点p'的左侧,那么l会覆
阅读全文
摘要:"题目链接" 容易看出是个最短路+DP。既然答案和天数有关,那么就令$f[i]$表示前$i$天最小成本。 这个转移很好想: $f[i]=\min(f[i],\ f[j]+cost(j+1,i)+K)$,$cost(j+1,i)$即第$j+1$天到第$i$天(使用同一道路)所需花费,即最短路,这个可以
阅读全文
摘要:"题目链接" 为什么这题网络流这么快, "海拔" 那题就那么慢。。 cpp //119968kb 544ms //路不是有向的,所以要建四条边。。既然如此就直接将反向边的流量设为w了。(or MLE...) include include include // define gc() getchar
阅读全文
摘要:"题目链接" 最小步数这类,适合用迭代加深搜索。 用空格走代替骑士。 搜索时记录上一步防止来回走。 不需要每次判断是否都在位置,可以计算出不在对应位置的骑士有多少个。而且每次复原一个骑士至少需要一步。 空格是不计算未复原骑士数的。 cpp //820kb 84ms include include i
阅读全文
摘要:"题目链接" $Description$ 求$$\sum_{i=1}^n\gcd(i,n)$$ $Solution$ $$ \begin{aligned} \sum_{i=1}^n\gcd(i,n) &=\sum_{d=1}^nd\sum_{i=1}^n[\gcd(i,n)=d]\\ &=\sum_
阅读全文
摘要:BZOJ 洛谷P4363 [Update] 19.2.9 重做了遍,感觉之前写的有点扯= = 首先棋子的放置情况是阶梯状的。 其次,无论已经放棋子的格子上哪些是黑棋子哪些是白棋子,之前得分如何,两人在剩下的棋盘上操作,结束时棋盘的状态也就是得分仍是确定的。 (记忆化不和先前的得分有关系啊,想清楚。)
阅读全文
摘要:$f[i]$为$Fibonacci$的第$i$项,求$$\prod_{i=1}^n\prod_{j=1}^mf[\gcd(i,j)]\mod (10^9+7)$$
阅读全文
摘要:md一个都没用到 fhqTreap还不知道哪写挂了。。
阅读全文
摘要:"题目链接" m个方程,n个未知量,求解异或方程组。 复杂度比较高,需要借助bitset压位。 感觉自己以前写的(异或)高斯消元是假的。。而且黄学长的写法都不需要回代。 cpp //1100kb 324ms include include include include const int N=10
阅读全文
摘要: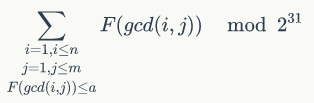 令$F(i)$表示$i$的约数和,求
阅读全文
令$F(i)$表示$i$的约数和,求
阅读全文
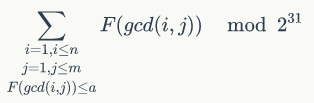 令$F(i)$表示$i$的约数和,求
阅读全文
令$F(i)$表示$i$的约数和,求
阅读全文
摘要:"题目链接" 题目是求最长反链,反链指点集内任意两点不能互相到达。 根据Dilworth定理,在DAG中,$$最长反链 = 最小路径覆盖 = V 最大匹配数$$ 用Floyd求一遍传递闭包后,在所有可互相到达的点间连边。求二分图最大匹配。 也可以这么理解: 每一条边表示这两个点不能同时被选中,选出最
阅读全文
摘要:"BZOJ" "洛谷" 裸01分数规划。二分之后就是裸最大费用最大流了。 写的朴素SPFA费用流,~~洛谷跑的非常快啊,为什么有人还T成那样。。~~ 当然用二分也很慢,用什么什么迭代会很快。 [Update] 19.2.15 下午写的zkw费用流在BZOJ上T了= = 然而在洛谷上和以前写的跑的差不
阅读全文
摘要:一道看过的模板题还写了半个小时。。
阅读全文
摘要:写个模板题怎么写的心力憔悴。。
阅读全文
摘要:求$$\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)为质数]$$
阅读全文
摘要:"题目链接" "后缀自动机做法见这(超好写啊)" 。 后缀数组是可以做的: 本质不同的字符串的个数为 $子串个数 \sum_{ht[i]}$,即 $\frac{n(n+1)}{2} \sum_{ht[i]}$. 如果是每次往后边插入字符,会改变SA[]。但如果向前边插入字符,相当于只加入了一个后缀。
阅读全文
摘要:"题目链接" 错位排列$D_n=(n 1) (D_{n 1}+D_{n 2})$,表示$n$个数都不在其下标位置上的排列数。 那么题目要求的就是$C_n^m D_{n m}$。 阶乘分母部分的逆元可以线性处理,不需要扩欧。 cpp //13516kb 6784ms include include i
阅读全文
摘要:"题目链接" 没有$D$的限制怎么做?"最小"我们可以想到最小割,把同一纵轴上的点串起来,分别连到S,T,最小割就是答案。(在这把点权放到前一条边上) 有限制,即如果要割点$i$,对于相邻纵轴只能去割$[i D,i+D]$。 用INF边限制住这个区间,即由$i$向$i D$连,由$i+D$向$i$连
阅读全文
摘要:三个月前整理的,已经忘得差不多了。。现在粘到这吧。~~(word打公式好累啊 markdown是真的好用啊。。)~~ ~~靠截得不好我想重截~~ 就是下面这些。$n$也可以写做$id$,无所谓啦。 $2.\ \sum_{d\mid n}\mu(d)=[n=1]$ $3.\ \sum_{d\mid n
阅读全文
摘要:求第$k$个无平方因子数
阅读全文
摘要:题目链接 洛谷 题目要求将数分成分成$m$段,使得下面这个式子最小($\mu=\frac{\sum_ma_i}$是平均数,$a_i$为第$i$段的和): \(\frac{\sum_{i-1}^m(\mu -a_i)^2}{m}*m^2\) $m$可以乘进去,得: \(m\times\sum_{i=1
阅读全文
摘要:"题目链接" 操作序列的顺序显然是无关的,所以只需按特定顺序求出一个长度为$l$的操作序列,它对答案的贡献为$l!$。 我们从小到大枚举所有选择。若当前为第$i$个,如果有一段长度为$2^i$不是+1+1这样递增的,那么需要把它分为两段长度为$2^{i 1}$的然后交换(在此之前满足所有长度更小的如
阅读全文
摘要:"题目链接" 不难看出矛盾关系可以构成一棵树,如果取一个节点,那么它的父节点就不能取,树形DP就行了。 这不是没有上司的舞会吗。。 但是漏了一种情况,即这个关系可能形成一个环(从n条边和样例能看出来),且有多个连通块,每个连通块一定且仅在根节点处有一个环。 在环上选择一条边断开,把端点分别作为根节点
阅读全文
摘要:"题目链接" 求最大的存活概率,DP+记忆化。 用f[s][x][y][hp]表示在s状态,(x,y)点,血量为hp时的存活概率。 s是个三进制数,记录每个陷阱无害/有害/未知。 转移时比较容易,主要是在陷阱未知时需要知道当前状态这个陷阱为有害/无害的概率,并用这两个概率相加。 如何求某个状态下未知
阅读全文
摘要:"题目链接" $Description$ 设$sum_i$表示$i$的二进制表示中$1$的个数,求$$\prod_{i=1}^nsum_i\ mod\ 10000007$$ $Solution$ 因为$n$的二进制有$logn$位,所以我们考虑枚举x,求满足$sum_i=x$的$i$的个数,然后就可
阅读全文
摘要:"题目链接" $Description$ 求$[l,r]$中$0,1,\cdots,9$每个数字出现的次数(十进制表示)。 $Solution$ 对每位分别DP。注意考虑前导0: 在最后统计时,把0的答案减掉对应位的即可,在第$i$位的前导0会产生额外的$10^{i 1}$个答案。 cpp incl
阅读全文
摘要:"题目链接" $Description$ 求$[1,n]$中十进制表示包含"13"这个子串,且能整除13的数的个数。 $Solution$ 数位DP: dp[位][s(pre/have"13")][remainder],上界由DFS状态记录. cpp //15MS 1520K include int
阅读全文
摘要:"BZOJ" "洛谷" $Solution$ 很显然的建二分图后跑最大费用流,但有个问题是一个数是只能用一次的,这样二分图两部分都有这个数。 那么就用两倍的。如果$i$可以向$j'$连边,$j$也向$i'$连边,如果上一次走了$i j'$,那么这一次一定走$j i'$。 每次跑最大费用流,直至有一次
阅读全文

 浙公网安备 33010602011771号
浙公网安备 33010602011771号