数构作业：图总结
数构作业：图总结
一.思维导图
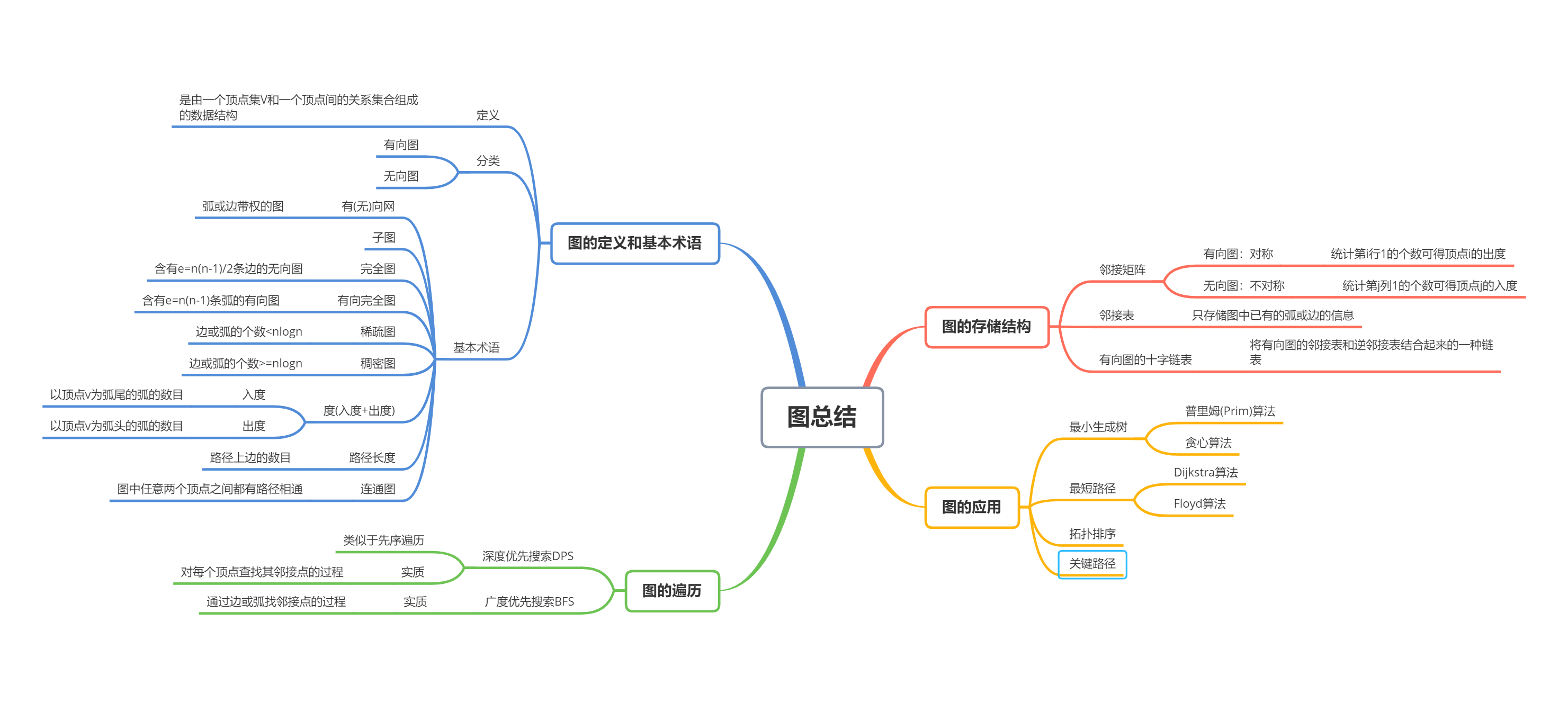
二.重要概念的笔记
1)图的表示
1.邻接矩阵
普通图：二维数组S[N][N] a[i][j]
特殊的无向图：一维数组S[(N(N+1)/2] a[i*(i+1)/2+j]
缺点：对稀疏图，浪费空间和时间，适合满图
2.邻接表
邻接表（一定要足够稀疏，才会省空间）
G[N]，每一行都是一个指针，指针指向一串链表，对应稀疏矩阵中的非0元素。
需要N个头指针 + 2E个结点（每个结点至少2个域），则E小于多少是省空间的？
N +2*2E<N*N
用邻接表表示有N个顶点、E条边的图，则遍历图中所有边的时间复杂度为:
O(N+E)
2)图的遍历
1.DFS
伪代码如下：
void DFS ( Vertex V ){
visited[V] = true;
for( V的每个邻接点W ){
if( !visited[W] )
DFS(W);
}
}
时间复杂度：
1)邻接矩阵存储 O(N^2)
2)邻接表存储 O(N+E)
优缺点：优点是内存消耗小；缺点是难以寻找最优解
2.BFS
伪代码如下：
void BFS ( Vertex V ){
visited[V] = true;
Enqueue(V,Q);
while(!IsEmpty(Q)){
V = Dequeue(Q);
for ( V的每个邻接点W ){
if ( !visited[W] ){
visited[W] = true;
Enqueue(W, Q);
}
}
}
时间复杂度同DFS：
1)邻接矩阵存储 O(N^2)
2)邻接表存储 O(N+E)
优缺点：优点是可以得到最优解；缺点是在树的层次较深并且子节点个数较多的情况下，消耗内存现象十分严重，因此，BFS适用于节点的子节点个数不多，并且树的层次不太深的情况
3)最小生成树之普里姆算法
void MiniSpanTree_P (MGraph G, VertexType u) {
//用普里姆算法从顶点u出发构造网G的最小生成树
k = LocateVex ( G, u );
for (j=0; j<G.vexnum; ++j )//辅助数组初始化
if (j!=k)
closedge[j] = {u,G.arcs[k][j].adj };
closedge[k].lowcost = 0;//初始，U＝{u}
for (i=0; i<G.vexnum; ++i) {
继续向生成树上添加顶点;
}
k = Min(closedge);//求出加入生成树的下一个顶点k
printf(closedge[k].adjvex, G.vexs[k]); //输出生成树上一条边
closedge[k].lowcost = 0;//第k顶点并入U集
for(j = 0; j < G.vexnum; ++j) //修改其它顶点的最小边
if (G.arcs[k][j].adj < closedge[j].lowcost)
closedge[j]={G.vexs[k], G.arcs[k][j].adj
}
三.疑难问题及解决方案
Dijkstra算法还有path数组
与求最短路相比，增加一个path数组，来记录最短路的路径
先将path[i]=-1，之后每次找出最短路的点p后将path[j]=p
用path[j]=i表示从i到j最短路的路径
for(int j=1; j<=n; j++){
if(!visited[j] && dis[p]+mapp[p][j]<dis[j]){
dis[j]=dis[p]+mapp[p][j];
path[j]=p;
}
}
算法代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxx = 999999999;
const int INF = 1e3 + 100;
int n, m;
int mapp[INF][INF];
int dis[INF];
int path[INF];
bool visited[INF];
void Dijkstra(int v0) {
for (int i = 1; i <= n; i++) {
dis[i] = mapp[v0][i];
visited[i] = 0;
path[i] = -1;
}
visited[v0] = 1;
for (int i = 1; i <= n; i++) {
int p, minn = maxx;
for (int j = 1; j <= n; j++) {
if (!visited[j] && dis[j] < minn) {
p = j;
minn = dis[j];
}
}
visited[p] = 1;
for (int j = 1; j <= n; j++) {
if (!visited[j] && dis[p] + mapp[p][j] < dis[j]) {
dis[j] = dis[p] + mapp[p][j];
path[j] = p;
}
}
}
return;
}
int main() {
while (cin >> n >> m) {
if (n == 0 && m == 0) break;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
mapp[i][j] = maxx;
}
}
int s, t, d;
while (m--) {
cin >> s >> t >> d;
mapp[s][t] = d;
}
Dijkstra(1);
for (int i = 2; i <= n; i++) {
if (i == 2) cout << dis[i];
else cout << " " << dis[i];
}
cout << endl;
for (int i = 2; i <= n; i++) {
cout << i;
int p = i;
while (path[p] != -1) {
cout << "-->" << path[p];
p = path[p];
}
cout << "-->" << "1" << endl;
}
}
return 0;
}
