多路查找树

多路查找树

1. 二叉树的问题分析

二叉树的操作效率较高，但是也存在一些问题：

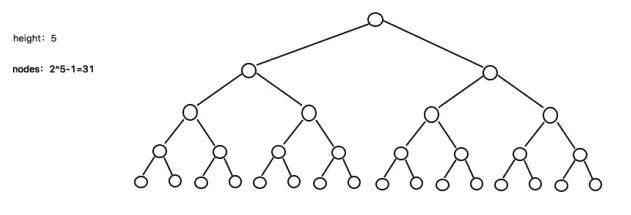
• 二叉树需要加载到内存中，若二叉树的节点较少没什么问题，但若二叉树的节点很多，则会出现下列的问题：
• 在构建二叉树时，需要多次进行I/O操作（海量数据存储在数据库或文件中），也即海量的节点在构建二叉树时速度有影响；
• 节点数量大，也会造成二叉树的高度很大，从而降低操作速度。

2. 多叉树

• 在二叉树中，每个节点都有数据项，且每个节点最多有两个子节点。若允许每个节点可以有更多的数据项和更多的子节点，就是多叉树（multiway tree）。
• 2-3树和2-3-4树都是多叉树，多叉树通过重新组织节点，减少了树的高度，从而能够对二叉树进行优化。
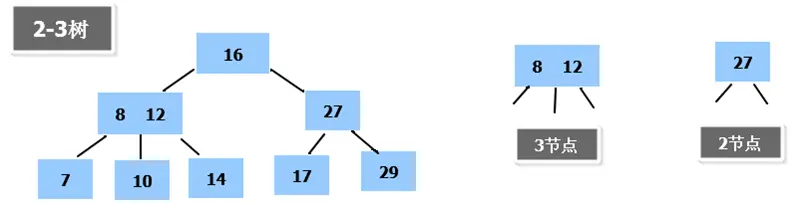
• 下图所示的一棵2-3树就是一棵多叉树：
  • 其中，2-节点定义为：包含1个数据项且有2个子节点；3-节点定义为：包含2个数据项且有3个子节点。

3. B树

3.1 B树的基本介绍

• B树通过重新组织节点，降低树的高度，并且减少I/O读写次数来提高效率；

• 文件系统及数据库系统的设计利用了磁盘预读原理，将一个节点的大小设为等于一个数据页（页的大小通常为4k），这样每个节点只需要一次I/O就可以完全载入；

  • 磁盘预读原理：当数据库需要频繁从磁盘上读取数据时，会产生较多的I/O等待，影响性能。为了避免这个情况，采用预读的机制，当读取的内存中还有若干页需要处理时，就开始触发磁盘预读，预读若干连续的数据页，从而提高效率。

• 将树的度M设置为1024，则在600亿个元素中最多仅需要4次I/O操作，就可以读取到想要的元素；

  • 树的度即为树中各个节点度的最大值，eg.对于二叉树而言树的度M就是2；
  • 由于一个节点仅需要一次I/O就可以完全载入，而\(1024^3 < 600亿 < 2014^4\)，因此最多仅需要4次I/O操作即可。

• B树和B+树广泛应用于文件存储系统以及数据库系统中。

• 下图中每个圆圈代表数据项，多个数据项连在一起表示的是存放这些数据项的节点。

3.2 2-3树

3.2.1 基本介绍

2-3树是最简单的B树结构，其满足以下特点：

• 2-3树的所有叶子节点都处在同一层（注：只要是B树就要满足该条件，也即B树的所有叶子节点都处于同一层）；
• 有1个数据项2个子节点的节点称为2-节点，2-节点要么没有子节点，要么就有2个子节点；
• 有2个数据项3个子节点的节点称为3-节点，3-节点要么没有子节点，要么就有3个子节点；
• 2-3树是由2-节点和3-节点组成的树；
• 注意：2-3树同样也满足类似BST的特性：
  • 对于2-节点，左子节点的元素 < 父节点元素 < 右子节点元素；
  • 对于3-节点，假设父节点元素分别为p1和p2，则有左子节点元素 < p1且p1 < 中间子节点元素 < p2且右子节点元素 > p2。

3.2.2 实际应用案例讲解

将数列{16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成2-3树，并保证数据插入的大小顺序。

插入规则：

1. 保证所有叶子节点都在同一层；
2. 整个2-3树只有2-节点和3-节点；
3. 当按照上述规则插入一个数据到某个节点时，若不能满足上面三个要求，就需要拆节点。先向上拆，如果上层满（即已经是有2个数据项的3-节点），则拆本层。拆后仍然需要满足上面3个条件；
4. 2-节点和3-节点相应的值的大小必须满足前述的特性。

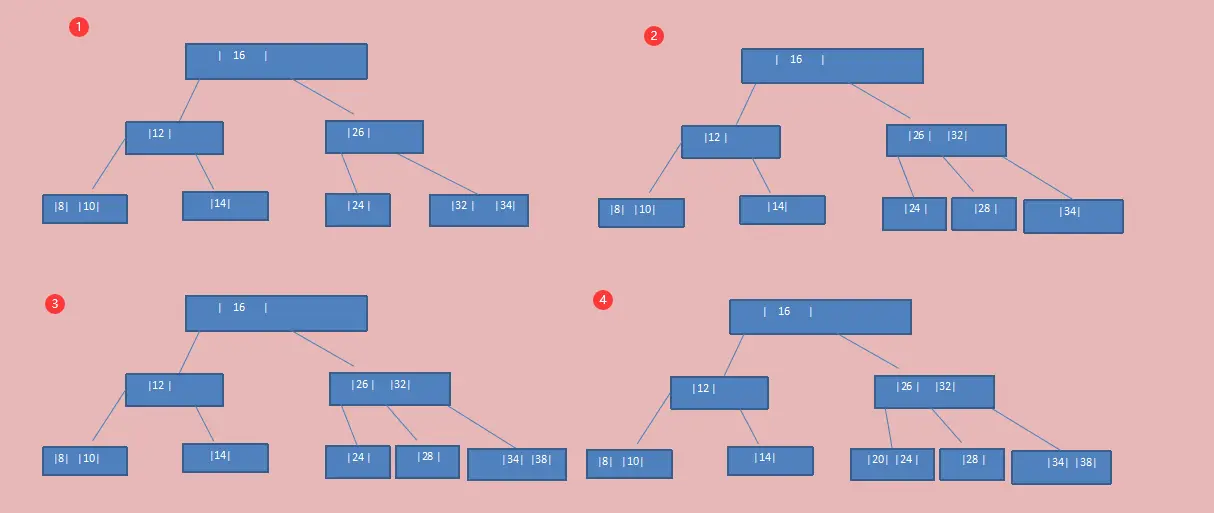
图解步骤：

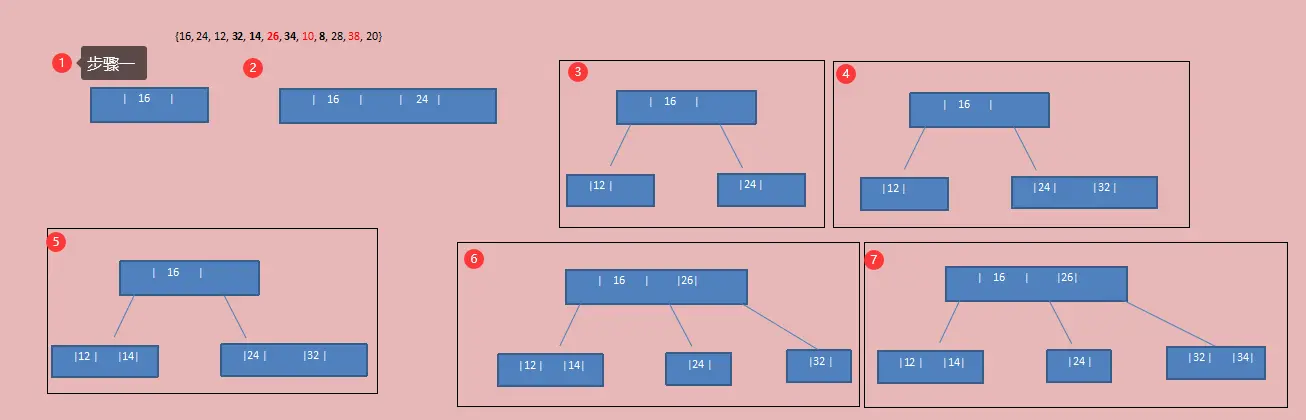
• 注意：上图中第6步插入数据26时，首先发现26 > 16，应放在{24，32}这个节点，但发现该节点已经是一个3-节点，再放入26就变成了4-节点，不满足要求，因此向上一层拆节点。此时若将24放入{16}这个节点，发现该节点并没有满足要求的中间子节点（即26 > 24），所以应将26放入上一层节点，{24}作为中间子节点使其满足16 < 24 < 26。

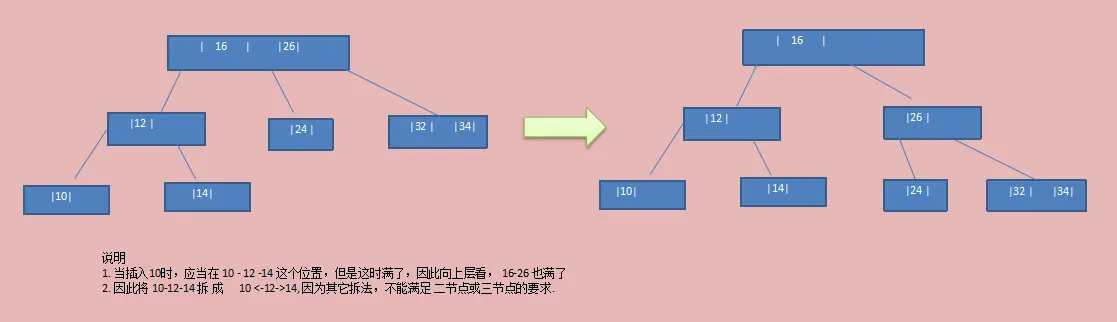
• 注意：当插入数据10时，本来应该上图第7步中{12，14}这个节点，但该节点已满，因此向上拆，但{16，24}这个节点也已满。所以拆本层的节点{12，14}，但拆完之后发现不满足所有叶子节点处于同一层这个要求。因此继续将{16，26}这个节点拆开。

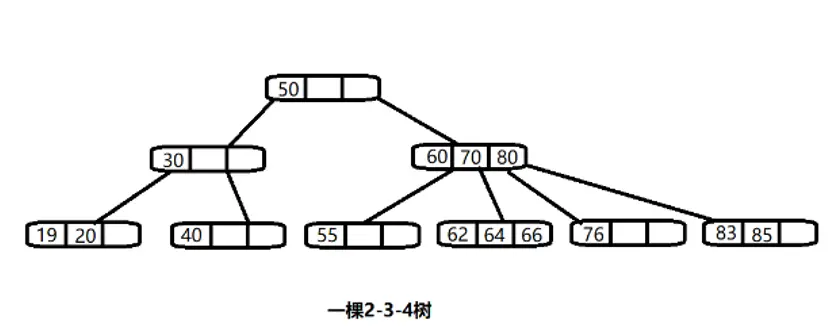
3.2.3 2-3-4树

除了2-3树，还有2-3-4树等其概念于2-3树类似，同样也是一种B树。

3.3 B树展开说明

B-Tree即B树，其中B表示Balanced，即平衡的意思。前面介绍的2-3树和2-3-4树都是B树的一种。在学习MySQL时，经常听到某种类型的索引是基于B树或者B+树的，B树的结构如下图所示：

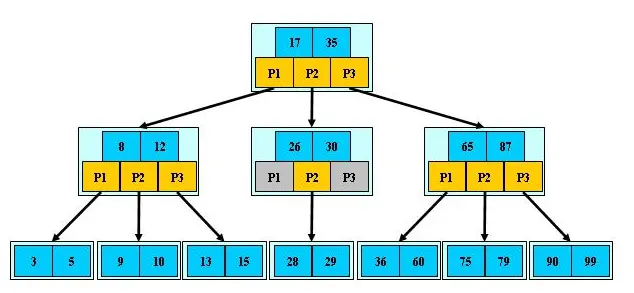
• B树的阶：即节点的最多子节点的个数，eg.2-3树的阶为3，2-3-4树的阶位4；
• B树的搜索，从根节点开始，对节点内的关键字序列（是一个有序序列）进行二分查找，若命中则结束，否则进入查询关键字所属范围的子节点进行查找。重复直至对应的指向子节点的指针为空，或者已经是叶子节点；
  • 注：上图中P1，P2，P3表示指向其孩子节点的指针。
• 关键字集合分布在整棵树中，即叶子节点和非叶子节点都存放数据。也即查找时既可以在非叶子节点命中也可以在叶子节点命中；
• 搜索有可能在非叶子节点结束，即查询的关键字在非叶子节点命中；
• 其搜索性能等价于在关键字全集内做一次二分查找。

4. B+树

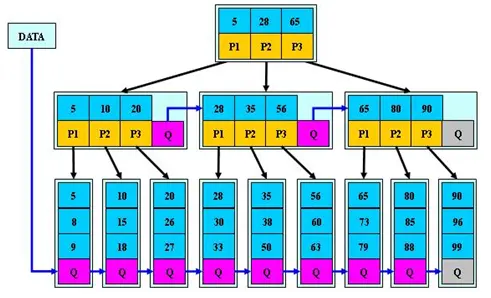
B+树是B树的变体，同样也是一种多路查找树，如下图所示：

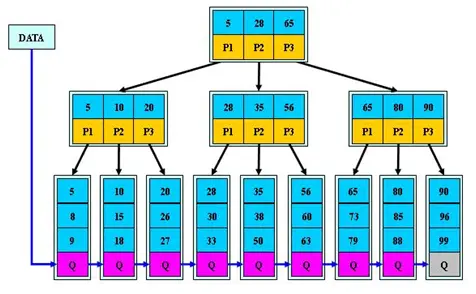
• B+树的搜索与B树基本相同，其性能也等价于在关键字全集中做一次二分查找；
• ❗B+树与B树的区别是：
  • B+树的所有关键字都存储在叶子节点的链表中，即数据只能在叶子节点（也称稠密索引），且链表中的关键字（数据）是有序的；非叶子节点相当于是叶子节点的索引（也称稀疏索引），叶子节点相当于是存储数据的数据层。
    • B+树只能在叶子节点命中，不可能在非叶子节点命中；而B树在查找时既可以在叶子节点命中也可以在非叶子节点命中；
    • 由于非叶子节点不存储数据，因此一般B+树的叶子节点和非叶子节点大小不同；而B树的每个节点大小一般是相同的，为一个数据页；
    • B+树的非叶子节点不存储数据，所有数据存储在叶节点导致其查询时间复杂度固定为\(O(logn)\)；而B树查询时间复杂度不固定，其与key在树中的位置有关；
  • B+树为所有叶子节点增加了一个链指针，即上图的Q；
    • B+树叶子节点两两相连，可以大大增加区间访问性，可以使用在范围查询等场景；而B树每个节点key和data在一起，无法区间查找；
  • 性能上，B+树比B树更适合实际应用中操作系统的文件索引和数据库索引。
• B+树和B树有各自的应用场景，不能说B+树完全比B树好，反之亦然。

5. B*树

B*树是B+树的变体，在B+树的非根节点和非叶子节点再增加了指向兄弟节点的指针，如下图所示：

• B*树定义了非叶子节点的关键字个数至少为：(2/3)*M，即块的最低使用率为2/3；而B+树的块的最低使用率为1/2；
• 也即B*树分配新节点的概率比B+树低，空间使用率更高。