Selectivity Estimation for Range Predicates using Lightweight Models

这次终于不用ai写总结了，总体来说这是一篇2018年的文章，用神经网络和树模型去拟合cost estimate，应该也是当时比较流行的算法

Introduction主要是喷了一波直方图在高维数据的表现不佳，因为数据库的feature之间可能存在相关性导致预估与实际的偏差较大，在这基础上提出的高维直方图在处理相关性上稍微好一些，但是需要更大的储存空间，也提出了一些直方图的优化思路比如说对于查询比较密集的区域建立更加频繁的桶，其余区域则建立比较稀疏的桶，但是总体来说直方图在高维的表现远不如一维

这时候就引出来树模型算法和神经网络算法，注意这里并不关注一维的ce，换句话说一维ce还是需要从直方图中得到。特种工程主要是将每个condition搞成(li,ri)的形式，如果这一维没有condition其实就是(min_i,max_i)，这样搞得话可以保证输入数据的都有相同形状。此外还引入了三个与相关性有关联的特征，这个可以直接从直方图计算得到。把这些作为输入也是希望模型可以学到不同条件之间的相关性的一些特征。至于label的话文章中采用了log运算，好处是可以将标签相对聚集在一起，避免因为一些太大的值而影响整个算法的关注点。

这是能想起来的一些内容，对数变换那里感觉可以着重记一下，所以还是让ai归纳了一下：

1. 减少相对误差（Reducing Relative Error）
   • 在选择性估计问题中，相对误差（如q-error）比绝对误差更为重要。对数变换能够使模型更关注相对误差，而不是绝对误差。具体来说，假设两个查询的实际选择性值分别为 s1​=20000 和 s2​=100，直接使用选择性值作为目标时，模型可能更倾向于减少对 s1​ 的预测误差，而忽略对 s2​ 的预测误差。通过对数变换，模型的目标是减少 log(s1​) 和 log(s2​) 的预测误差，这使得模型对不同量级的选择性值给予相同的关注。
   • 从数学角度来看，对数变换将目标值的范围压缩到一个更小的区间，使得模型在训练过程中能够更均匀地处理不同量级的选择性值。
2. 优化目标（Optimization Objective）
   • 对数变换后的目标值 log(si​) 使得模型的优化目标更接近于最小化相对误差。具体来说，最小化均方误差（MSE）在对数空间中等价于最小化相对误差的平方。这可以表示为：

     

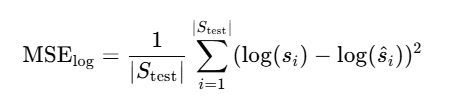     其中，si​ 是实际选择性值，s^i​ 是模型预测的选择性值。最小化这个目标函数能够使模型在对数空间中更均匀地处理不同量级的选择性值，从而减少相对误差。
3. 模型的适应性（Model Adaptability）
   • 对数变换使得模型能够更有效地处理选择性值的巨大变化。例如，在神经网络中，对数变换后的目标值使得每个局部线性函数能够更灵活地适应不同量级的选择性值。具体来说，假设在一个局部区域内，模型学习到的线性函数为：

     

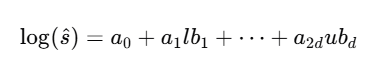     通过指数运算恢复为原始的选择性值后，模型的预测值为：

     

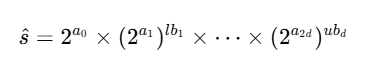     这种对数线性函数能够更好地适应选择性值的巨大变化，使得模型在不同量级的选择性值上都能保持较高的预测准确性。
4. 对基于树的集成方法的影响（Impact on Tree-based Ensembles）
   • 对于基于树的集成方法（如XGBoost），对数变换后的目标值能够更有效地聚合不同树的预测值。在没有对数变换的情况下，不同树的预测值可能差异很大，导致最终的聚合值主要由少数几个树的预测值决定。通过对数变换，每个树的预测值在对数空间中被更均匀地处理，从而使得每个树都能对最终的预测值产生更均衡的影响。这不仅提高了模型的预测准确性，还使得模型能够更有效地利用所有树的预测能力。